Оглавление:





Трение и теплоотдача в ламинарном пограничном слое
- Интегральное уравнение энергии (VI1-38) используется для исследования теплопередачи пластины, когда она течет в продольном направлении вокруг потока с постоянной rate. In в пластине имеется неотапливаемый начальный участок длиной x, который равен температуре основного потока, Т^.Температура нагретой части пластины равна To to>(рис. VII-7).
Ламинарное движение жидкости пограничного слоя по поверхности пластины. Динамический пограничный слой начинает развиваться от передней кромки пластины(x-0), а тепловой пограничный слой начинается от начала нагреваемого участка (x =xib. It трудно определить коэффициент теплопередачи путем прямого интегрирования уравнения пограничного слоя в этих условиях, то есть получить точное solution. It почти решает проблему. Pr I (газ Pr 1, жидкий металл Pr — > 0, жидкость PR> I, масло Rg oo).
Фактически к этому результату пришёл уже Сади Карно в сочинении «О движущей силе огня и о машинах, способных развивать эту силу». Людмила Фирмаль
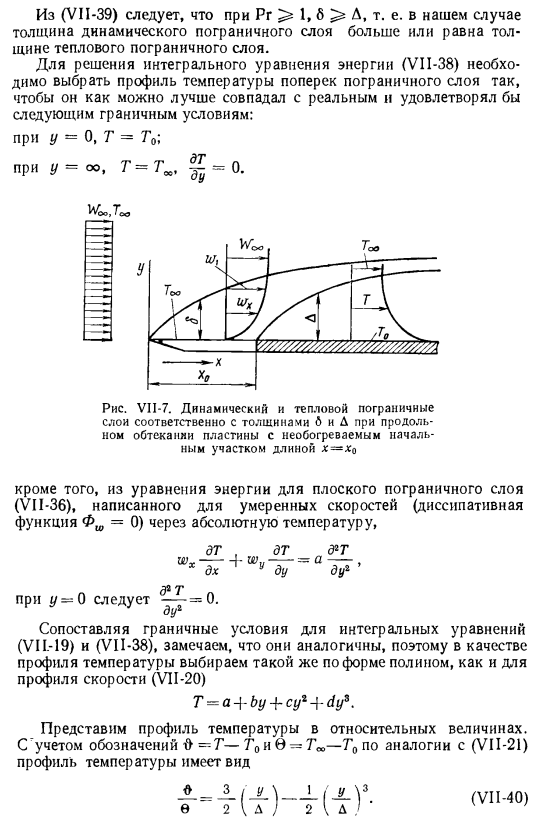
Анализируя уравнения движения и энергии плоского потока, он набухает[881. И_ _ 1 6 р РГ (В VII-39) Из (VI1-39) видно, что для Pr> 1, 6> A, то есть в этом случае толщина динамического пограничного слоя больше толщины теплового пограничного слоя. Для решения интегрального уравнения энергии (VI1-38) необходимо выбрать температурный профиль всего пограничного слоя、 Постарайтесь максимально точно соответствовать следующим граничным условиям: fort / = 0, T = To; для г = ОО, Т = Тл — м Натуральная и довольны Рис VII-7.
Динамический и термический пограничные слои толщиной 6 и D соответственно продольно обтекают пластину с неинициальным нагревательным участком длиной x-x Далее из уравнения энергии плоского пограничного слоя (VI1-36), описываемого с умеренной скоростью (диссипативная функция Phi} = 0) через абсолютную температуру、 Д2Т. ду’ для y-0,^ — ^ — = 0. ч /2 Интегральные уравнения (VII. сравнивая граничные условия (-19) и (VII-38), мы видим, что они аналогичны.
Поэтому в качестве профиля температуры выберите полином той же формы, что и профиль скорости (VII-20). Т = а + + ТИЦ * + ды *. Пусть температурный профиль выражается как относительный value. By по аналогии с обозначениями О=Г-То и 0 = −7 ′ ₀ и (vi1-21), температурный профиль принимает вид: ± ₌ ± / М _ _ _ _ _ LfJLV 8 2 \ D! 2 \ Д / (В VII-40) Вычислите Интеграл, который падает слева от выражения (VI1-38). для этого подставьте значения (VII-40) 0 и (VII-21) wₓ в подынтегральное выражение.
- Выполните Интеграл в пограничном слое (если y> A, то подынтегральная функция равна нулю).Введем обозначение r — *- (в этом случае вспомним r I). в результате、 3 3 3 ’^b ’ f2280 означает= 0.Потом он ушел. Часть интегрального уравнения энергии (VI1-38) может быть выражена в следующем виде: Вычислите правую часть уравнения (VI1-38).Для этого дифференцируем выражение (VI1-40) относительно y и устанавливаем y = 0, чтобы получить желаемый результат.
Второе начало термодинамики задаёт ограничения на направление процессов, которые могут происходить в термодинамических системах, и исключает возможность создания вечного двигателя второго рода. Людмила Фирмаль
Подставляя результат вычисления слева и справа от интегрального уравнения энергии (VI1-38), получаем: — 0оо ^»,-(g26)- 20 v⁷ ДХ После дифференцирования и сокращения, окончательное выражение принимает вид — wjr4 = а. 10 \ ДХ) Используя результаты, полученные при решении интегральных уравнений динамических пограничных слоев 6 и J6, примем эту формулу следующим образом: / −3 4 га. 13/1、 ДХ V / а Возьмем в последней формуле 13/14 = 1 и рассмотрим ее-Pr、 gzgaga^₌; ± ₁ ДХ РГ .
Общая форма решения этого дифференциального уравнения является с. ₌ГЗ cx⁴- rg. определим интегральную константу C с помощью граничного условия r-0 из x-xx и подставим ее значение в общее solution. As итог、 (В VII-41) Если пластина нагревается по всей своей длине, то есть если нет неотапливаемой части, то x₀ — = 0, а (VI1-41) равно Р = РГ Формула (VI1-41) была получена при Pr> I, но она дает удовлетворительные результаты при 0,5 Pr 1 136.
Теперь определим плотность теплового потока Q от пластины к жидкости. Для ламинарных пограничных слоев на основе законов Фурье (I-Za) и Ньютона (1-7)、 Используя зависимость температурного профиля φ / 0 ^(VI1-40), толщины динамического пограничного слоя 6 (VII-23) и соотношения r = — y, получим формулу, которую определим из последней Формулы. Уже разделив число нуссельта Nuₓ с локальным коэффициентом теплопередачи| 36): 0,322?.Х1. и так далее. 0.322 Ке] /2Рг1/3 ■;?1/3. (В VII-42).
Если пластина нагревается по всей своей длине, то есть нет неотапливаемой области (x-0), то формула (VI1-42) принимает вид Нуₓ=0. 323Rey2Pr / 3. (В VII-43) В результате правильного решения уравнения ламинарного пограничного слоя с Pr = I (VI1-43) получаем уравнение, отличающееся постоянным коэффициентом. Nuₓ= 0,332 Rel / 2Rg1 / 3. (В VII-44) Формула для определения среднего числа нусселей на пластине длиной l и шириной 1 получена с использованием следующего соотношения: Ну = — JNuₓdx.
О Подставляя значение Nuₓ в выражение (VI1-43) в последнее отношение, получаем искомое выражение. Nu =0.646 Не,/2рг, / 3. (В VII-45) Это указывает на то, что существует связь между локальным коэффициентом теплопередачи и / или локальным трением coefficient. To для этого разделите обе стороны формулы (VII-44) на произведение 2 опорных Pr. Nuₐ0.332. РГ Ре-УйёРг2/3 ′ (В VII-46).
Левая сторона полученного соотношения представляет собой безразмерный комплекс, называемый числом Стэнтона、 Нуи._______ вопрос._ Пр-Ре» — П ^ ВП (Тоже-Г、)」 (В VII-47) Учитывая принятые обозначения и выражение (VI1-46), выражение (VII-47) можно представить в виде: Святой^ — = Два (В VII-48) Критерий Прандтля Pr = 1 (VII-48a) Среднее Количество Ст Стэнтон = Это место a-средний коэффициент теплопередачи), а средний коэффициент трения Su Pr-1 равен (В VII-486).
Смотрите также:
| Уравнение энергии для пограничного слоя | Турбулентный пограничный слой |
| Интегральное уравнение энергии для пограничного слоя | Уравнения турбулентного пограничного слоя |

