Оглавление:


Трение цапф в подшипниках
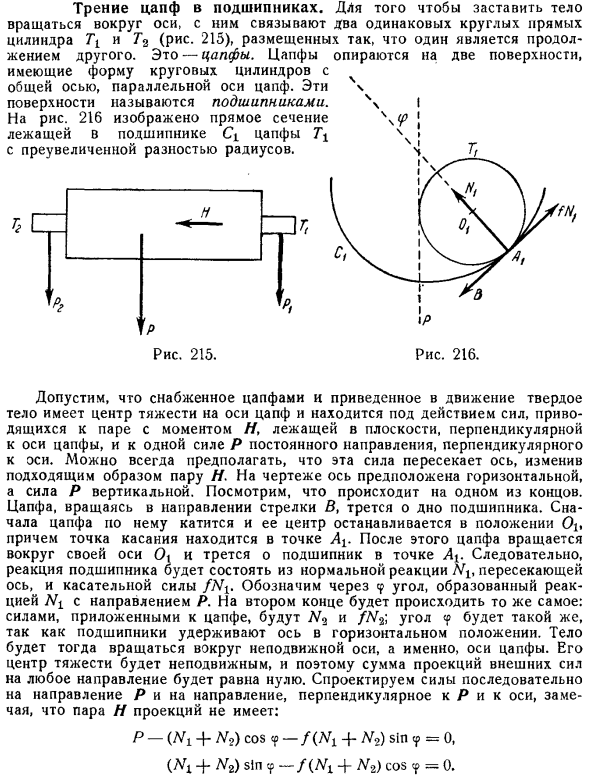
- Для вращения корпуса вокруг своей оси соединены 2 одинаковых прямых цилиндра 7 и 7 2 рис.215, расположенных таким образом, что один из них является продолжением другого. Это цапфы. Цапфа расположена на 2 поверхностях в виде цилиндра с общей осью, параллельной оси цапфы. Эти поверхности называются подшипниками. Я рис. 216 показан прямой части. Преувеличенный подшипник оси радиуса. 216. Рисунок 215. Предположим, что твердое тело с цапфой имеет центр тяжести на оси цапфы и находится под действием момента H в плоскости, перпендикулярной оси цапфы, и силы, которая связывает с 1 силой P в постоянном направлении, перпендикулярном оси цапфы.
Формы уравнений связей в неголономных системах. Невозможность прямого применения уравнений Лагранжа к минимальному числу параметров. Людмила Фирмаль
Можно предположить, что эта сила всегда будет пересекать ось и изменять пару I appropriately. It предполагается, что ось на рисунке горизонтальна, а сила P вертикальна. Давайте посмотрим, что происходит на одном конце. Ось, вращающаяся в направлении стрелки B, царапает нижнюю часть подшипника.
- Сначала ось вращается вдоль нее, затем ее центр останавливается в положении Oy, и после того, как точка касания находится в этой точке. Ось вращается вокруг своей оси O и трется с подшипником в точке A .в результате реакция подшипника состоит из нормальной реакции Ny и тангенциальной fNy поперек оси. Относится к реакционному формованному углу с направлением Ni P в cp. То же. Потому что подшипник держит ось в горизонтальном положении. Тело вращается вокруг неподвижной оси, то есть оси оси. Его центр тяжести неподвижен, поэтому сумма проекций внешних сил во всех направлениях будет равна нулю. Непрерывно проецируйте силу в направлении P и в направлении, перпендикулярном оси P.
Приложение к относительному движению тяжелой системы по отношению к Земле, принимая во внимание также вращение Земли. Людмила Фирмаль
Обратите внимание, что пара проекций H не имеет следующего P A 4 A 2 cos Ni 4 W2 sin cp = 0, из 2 го выражения находим tan p f. As в результате cp равен углу трения. Тогда Тан из первого уравнения Если вы замените его на: М + 2 = с COS Р. Здесь мы применяем теорему момента на оси Штыря, чтобы получить уравнение движения. Mk2 показывает момент инерции вокруг этой оси через o угловую скорость и радиус P контакта. w24g = P LG1 + l 2 Или наконец то =И опсин р. В При составлении этого уравнения необходимо было отметить, что сумма моментов обеих сил, составляющих пару относительно оси, в точности равна моменту H.
Смотрите также:
Теоретическая механика — задачи с решением и примерами
Если вам потребуется заказать теоретическую механику вы всегда можете написать мне в whatsapp.

