Оглавление:
Как оптимально организовать поставку грузов от поставщиков к потребителям (транспортная задача)
Симплекс-метод дает возможность решить любую задачу линейного программирования. Однако существует много методов, которые учиты вают конкретные особенности каждой из этих задач, а потому более эффективных. В качестве примера одной из таких задач рассмотрим транспортную задачу.
Задача:
Перевозится однородный груз из трех пунктов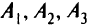 
к четырем местам назначения 
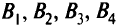. Из пункта 
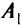может быть отправлено 50 т, из 
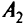— 40 т, из 
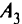— 20 т. При этом в пункт 
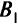должно поступить 30 т груза, 
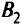— 25 т, 
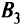— 35 т, 
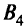— 20 т. Расстояния 
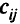от 
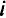-го поставщика до 
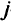-го потребителя приведены в углах клеток табл. 2.6;
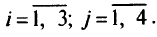
Необходимо составить план перевозки, обеспечивающий наименьший общий пробег транспорта в тонно-километрах при условии, что все запасы должны быть вывезены, а потребитель получит точно необходимое количество груза.
Мы сформулировали сбалансированную транспортную задачу, когда количество груза у поставщиков равно потребности потребителей. Несбалансированная транспортная задача сводится к сбалансированной путем введения фиктивного поставщика, если потребности превышают предложения, или фиктивного потребителя в противном случае. Расстояния в фиктивной строке (столбце) указываются равными нулю. Сбалансированная и несбалансированная задачи решаются по одному алгоритму.
Решение. Пусть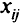 
— количество груза, которое будет доставлено из 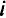-го пункта отправления в 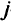-й пункт назначения; 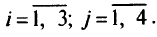. Целевая функция задачи — минимизировать общий пробег транспорта в тонно-километрах
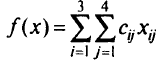
при условии, что весь груз от поставщика должен быть вывезен —
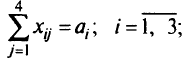
каждый потребитель получит необходимое ему количество груза—
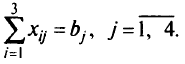
Особенностью задачи является тот факт, что в матрице ограничений все коэффициенты при неизвестных равны единице. Это облегчает все вычисления по симплекс-методу.
Число переменных в данной задаче равно в общем случа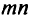е 
, где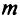 
— число поставщиков, 
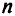— число потребителей. Число уравнений в системе ограничений равно 
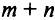. Однако нетрудно видеть, что одно из этих уравнений может быть получено из других. Так, если определены наличие груза у всех отправителей и потребность всех получателей, кроме одного, то спрос последнего легко установить как разность между общим запасом и общей потребностью остальных получателей, т.е. система ограничений содержит 
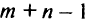независимых уравнений с 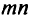неизвестными. Число базисных переменных также будет 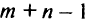,остальные переменные — свободные.
Алгоритм решения транспортной задачи сопоставим с алгоритмом симплекс-метода.
1. Нахождение допустимого базисного (опорного) решения. В транспортной задаче его находят довольно просто одними из двух методов.
А. Метод северо-западного угла — удовлетворяем потребность первого потребителя за счет первого поставщика; если потребности оказались выше возможностей первого поставщика, то подключаем второго поставщика. Если запасы первого поставщика выше потребностей первого потребителя, то остаток запасов первого поставщика передаем второму потребителю и т.д. Мы должны заполнить 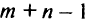клетку. Может оказаться, что число заполненных клеток меньше 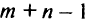(случай вырождения). Тогда клетки, недостающие до 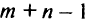, заполняем нулями (эти клетки выбираем произвольно) — это так называемые условные поставки. Процесс получения опорного решения нашей задачи методом северо-западного угла представлен в табл. 2.7.
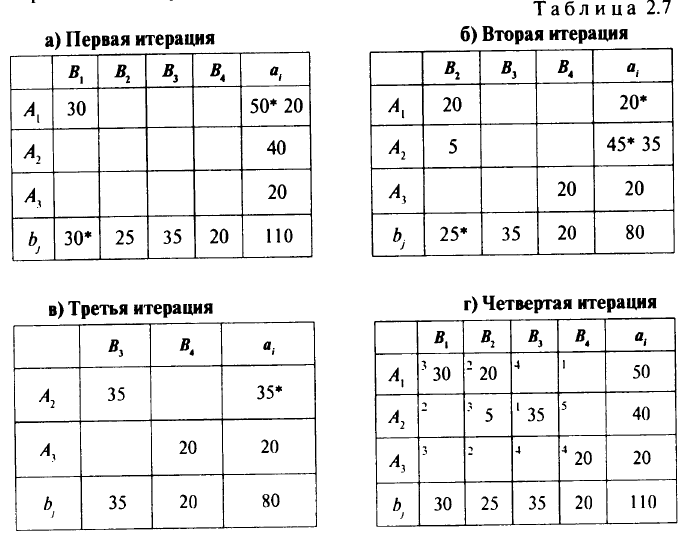
Примечание. Помеченные (*) значения следует читать как зачеркнутые цифры.
За четыре итерации мы заполнили в таблице перевозок пять клеток вместо шести, но удовлетворил и условиям-ограничениям. Надо ввести нулевую клетку — условную поставку. Пусть это будет клетка(1, 4):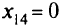
. Получили опорное решение:
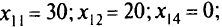
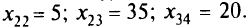
Значение целевой функции при таком решении
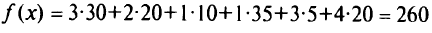
(тонно-километров);
Б. Метод учета наименьших расстояний (стоимостей) перевозок аналогичен методу северо-западного угла, только в первую очередь заполняются те клетки, для которых указанные расстояния (стоимости) наименьшие.
- Проверка полученного плана перевозок на оптимальность.
С этой целью рассмотрим двойственную задачу к поставленной транспортной задаче. В качестве двойственных переменных введем величины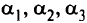 
, соответствующие первым трем ограничениям, и 
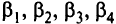— для остальных ограничений. Эти переменные называют потенциалами.
Целевая функция двойственной задачи: максимизировать
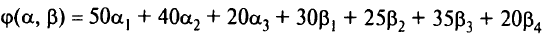
при условии (для базисных клеток)
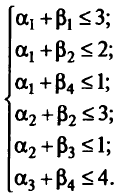
Для оптимального плана исходной задачи условия-ограниче-ния двойственной задачи выполнялись бы как равенства, так как согласно условиям дополняющей нежесткости, если в оптимальном плане исходной задачи значение какой-либо переменной строго больше нуля, то соответствующее ограничение двойственной задачи при подстановке в него оптимального плана становится равенством. Получим систему (2.3) из шести уравнений с семью переменными. Поскольку независимых переменных в данной системе ровно 3 + 4 — 1 = 6, то одна переменная свободная. Пусть это будет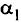 
. Положим а, = 0, получим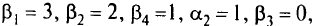 
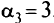. Составим таблицу перевозок для данной итерации (табл. 2.8). Полученное решение 
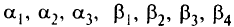подставляем в ограничения двойственной задачи, не вошедшие в систему уравнений (2.3), т.е. соответствующие пустым клеткам. Если эти ограничения являются верными неравенствами для найденного решения, то проверяемый допустимый план исходной задачи является опти-
мальным. В противном случае — не является. Для пустых клеток имеем
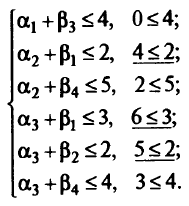
Второе, четвертое и пятое неравенства являются неверными, поэтому решение не будет оптимальным. Необходимо провести улучшение плана.
- Составление нового допустимого плана. Наметив свободную переменную, которую надо перевести в базисную, определим базисную переменную, переводимую в свободные. Переменные, соответствующие свободным клеткам (2, 1); (3, 1) и (3, 2), в которых неравенства (2.4) нарушаются, могут быть переведены в базисные. Выбираем клетку (3,2). В симплекс-методе для выбора генерального элемента требуется рассмотреть положительные отношения в столбце
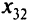. В матрице перевозок положительные коэффициенты в столбце 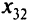равны +1 и отвечают тем базисным клеткам, которые соответствуют отрицательным вершинам некоторой замкнутой ломаной линии, называемой циклом пересчета для 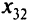. Следовательно, генеральным элементом является базисная переменная из числа отвечающих отрицательным вершинам цикла пересчета, значение которой минимально.
Цикл пересчета — это замкнутая ломаная линия, начинающаяся в свободной клетке, все остальные вершины которой помещены в базисные клетки и соединены звеньями, лежащими вдоль строк и столбцов матрицы.
В каждой вершине встречаются только два звена, причем одно из них расположено по строке, другое — по столбцу. Никакие три вершины, встречающиеся подряд при обходе, не лежат на одной прямой. Если циклом служит самопересекающаяся линия, то точки самопересечения не могутбытьее вершинами. Свободной клетке в цикле присваивают знак «+», другим вершинам — чередующиеся по ходу знаки «—», «+», «-» и т. д. Построим цикл пересчета для свободной клетки (3,2) (табл. 2.9). В отрицательных вершинах цикла пересчета стоят два числа: 20, 20; минимальное из них 20. Так как число положительных и отрицательных вершин одинаково, то баланс не нарушится, если в отрицательных вершинах вычесть число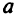 
, а в положительных вершинах прибавить это же число 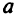. Вычитая минимальное из чисел, стоящих в отрицательных вершинах, мы получаем новую свободную переменную 
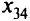, а базисной станет 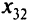. Прибавим 20 в положительных вершинах цикла, вычтем 20 в отрицательных вершинах и получим допустимое решение, представленное в табл. 2.10.
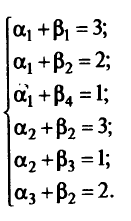
Пусть 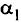= 0, получим
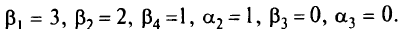
Очевидно, что для клетки (2, 1) неравенство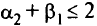 
не выполняется: 
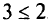, т.е. данное решение не является оптимальным. Шаги 3 и 4 повторяем до тех пор, пока не достигнем оптимального решения.
Цикл пересчета для клетки (2, 1) показан в табл. 2.10. Третье допустимое решение приведено в табл. 2.11.
Здесь же показаны значения рассчитанных для данной итерации потенциалов. Нетрудно убедиться, что для всех свободных клеток сумма потенциалов меньше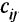 
, т.е. получено оптимальное решение. Оно означает, что от первого поставщика к первому потребителю надо перевезти 25 т груза, ко второму 5 т, к четвертому 20т; от второго поставщика надо перевезти к первому потребителю 5 груза, к третьему 35 т; от третьего поставщика надо перевезти 20 т груза только ко второму потребителю. Минимальное значение целевой функции 
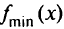=3 25 + 2-5 + I -20 + 2-5 + 1 -35 + + 2-20 = 190 (тонно-километров).
Эта теория взята со страницы лекций по предмету «математическое программирование»:
Предмет математическое программирование
Возможно эти страницы вам будут полезны:
