Пример №5. Транспортная задача.
Имеется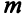 
поставщиков и 
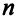потребителей некоторого товара. Запасы 
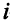-го поставщика составляют 
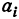единиц товара, 
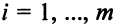. Потребности 
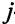-го потребителя равны 
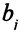единиц товара, 
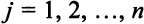. Стоимость перевозки единицы товара от 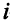-го поставщика 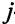-му потребителю равна 
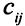единиц. Требуется так закрепить поставщиков за потребителями, чтобы минимизировать суммарные затраты на перевозку товара.
Описание неизвестных. Здесь неизвестно, сколько единиц товара должен каждый поставщик передать каждому потребителю. Обозначим через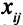 
количество единиц товара, поставляемых 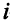-м поставщиком 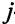-му потребителю,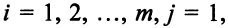 
. Всего неизвестных 
.
Описание целевой функции. Определим суммарные затраты на перевозку товара. Например, затраты на перевозку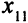 
единиц товара от первого поставщика первому потребителю равны произведению 
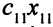. В общем случае затраты на перевозку 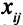единиц товара от 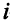-го поставщика 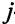-му потребителю равны произведению 
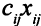. Суммарные затраты равны
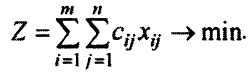
Описание системы ограничений. Будем считать, что сумма всех запасов не меньше суммы всех потребностей:
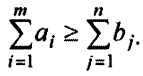
Тогда ограничения сводятся к требованию удовлетворить потребности каждого потребителя и к условию невозможности вывезти от каждого поставщика больше, чем есть у него в запасе.
Первый поставщик вывозит всем потребителям
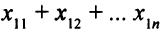
единиц товара. Таким образом,
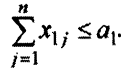
Так как поставщиков всего 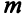, то число ограничений по запасам равно 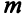. Для 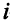-го поставщика имеем:
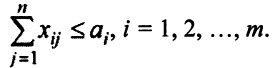
Опишем ограничения по потребностям. Первый потребитель получает от всех поставщиков
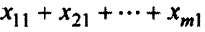
единиц товара. Тогда должно быть
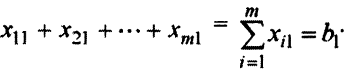
Число ограничений по потребностям равно 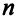, так как всего 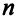потребителей. Для 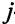-го потребителя имеем:
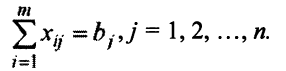
Кроме того, величины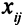 
не могут быть отрицательными,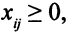 
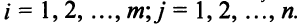
Эта задача взята со страницы решения задач по предмету «линейное программирование»:
Решение задач по линейному программированию
Возможно эти страницы вам будут полезны:
| Пример №3. Задача о смеси. |
| Пример №4. Задача планирования производства. |
| Пример №6. Минимизация дисбаланса на линии сборки. |
| Пример №7. Построить допустимую область системы неравенств |
