Трансцендентные функции

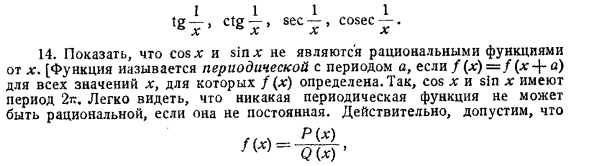
Трансцендентные функции

• Трансцендентальная функция. Все не x-алгебраические функции x называются трансцендентными функциями. Это определение относится к отрицательному типу. Установите y = 1, если x рационально, и y = 0, если x невозможно. Граф состоит из двух рядов точек на линиях y = 1 и y = 0. На первый взгляд это неразличимо от этих двух последовательных линий, но на практике в каждой есть бесконечно много точек. 11. Если x невозможно, установите y = x и y =: J, f ”, если x- р Рациональный номер.

Теперь рассмотрим рациональное значение х. Первый х Положительно. Далее, для | / j «^ j», pfc *, 1C равно plq. д. е. Поэтому все точки соответствуют рациональным числам Значение x не находится на линии y-x, за исключением единственной точки (1, 1). Кроме того, если P <4, Очевидно, что если 0 1, когда х> 1, 1 / приблизительно g (I q) Вы можете найти любое количество рациональных чисел с большими числителями и знаменателями около любого значения, равного x.

Часть графика, соответствующая необоснованному значению x, на самом деле не является непрерывной кривой, но она неотличима от прямой линии y = x по внешнему виду. Людмила Фирмаль

Поэтому граф содержит большое количество точек, которые накапливаются вокруг прямой y = x. Его общая форма (для положительного x) — это линия, окруженная группой изолированных точек, и она становится толще по мере приближения к линии. Часть графика, соответствующая отрицательным значениям x, состоит из остальной части линии разрыва и зеркального отображения всех этих изолированных точек на оси «v-s». Таким образом, на левой стороне оси y точки накапливаются вокруг линии y-x, принадлежащей графу, а не вокруг линии y = x>.

Вот систематическая классификация трансцендентных функций, но вы можете выбрать один или два особенно важных подкласса. E. Прямые и обратные тригонометрические или круговые функции. Это основные тригонометрические синус и косинус, их инверсии и производные от них функции. Пока можно предположить, что читатель знаком с наиболее важными характеристиками *). Пример XV. 1. Нарисуйте график функции cos l: sin xt a Cos * -f-b sin x. [cos x-> sin a * = 0 cos (a * -a). Где p = y a — \ — £ 2 и a есть б) Знак и знак равны •, ■ — и соответственно графу ‘ya * + jt var + p Ки этих трех функций по существу схожи. ) 2.

• Решение задач по высшей математике

Явные алгебраические функции	Графическое решение уравнений, содержащих одно неизвестное число
Неявные алгебраические функции	Функции двух переменных и их графическое представление

Примеры решения и задачи с методическими указаниями

Решение задач	Лекции
Сборник и задачник	Учебник

• Нарисуйте график функции cos * dg, sina.v, cos5x -] — b sin2 x. 3. Предположим, что графики f (x) и F (x) нарисованы. Далее график функции / (X) cos2 x F (x) sin * a- Представляет волнистую кривую, которая колеблется между кривыми y — f (x) и y — F (x). Нарисуйте этот график, если f (x) = x и F (x) = x *. 4. Указывает, что график функции cos px -} — cos qx находится между графиками функций 2 cos £ (p-q) x и -2 cos [p-q-q) x и касается каждого из них. Очередь. Если графиков мало, дайте обзор. (Пример 1908) 5. Нарисуйте график функции ,. 1 ,,. Грех л: x -f- sin Xy-hsin *, dg sin X.-. Х х 6. Нарисуйте график функции sinу. [Если y = sin-, y = 0 — это x-, а m — любое целое число. х Кроме того, если x = —————, y-1, если g = -y——, y = -1. кривая

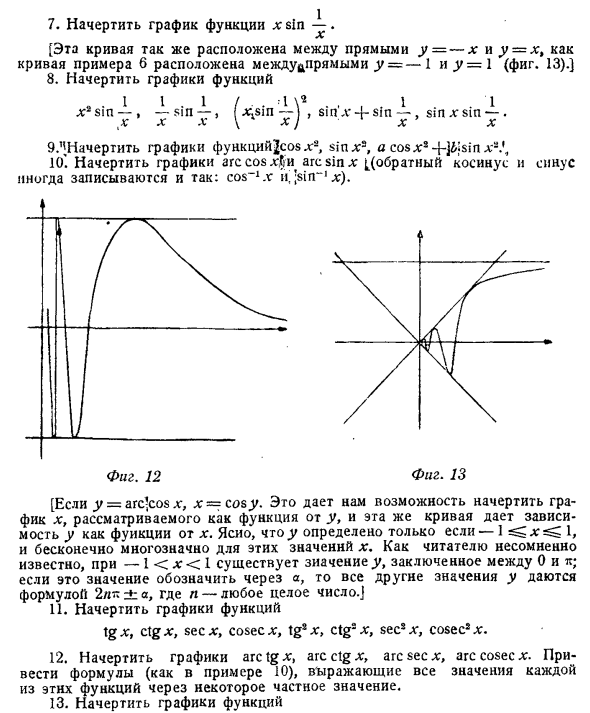
Это колеблется, и частота колебаний увеличивается, когда х приближается к нулю. Если x = 0, функция u определена. Если х большой, у мал 8). Отрицательная половина кривой ведет себя аналогично. ] Нарисуйте график функции xsin. [Эта кривая находится между линиями y = -x и y = x, потому что кривая в примере b находится между линиями y = -1 и y = 1 (рисунок 13). ) 8. Нарисуйте график функции x2 sin ~, sin-, (xxsin -M, sin l- -f sin-, sin * sin-.t K X L \ x y X X 9. «Нарисуйте график функции ^ Sovx8, sinx2, cosx * -f-J & sinх3.», 10 ‘. Дуга cos x $ и дуга sinx [(обратный косинус и синус являются cos-1 x и,; sin ~ ‘x) могут быть записаны.

Он полностью находится между прямой = -1 и yy = 1 (рисунок 12). Людмила Фирмаль

Та же фигура. Рис. 12 13 Я [Если y = arc’cos x, x = уютно. Это дает вам возможность нарисовать график x, который можно рассматривать как функцию от y, а та же кривая дает зависимость y как функцию от x. Очевидно, что у определяется только при -1 ^ х ^ 1 и неопределенно неоднозначно для этих значений х. Как вы определенно узнаете, если -1 <x <1, значение y находится между 0 и k. Если это значение обозначено как a, все остальные значения y задаются выражением 2n ± .a, где n — любое целое число. 11. Нарисуйте график функции tg *, ctgx, secx, cosecx, tg’x, ctg2x, sec5 *, cosec * x. 12. Нарисуйте график arctgx, arcctgx, arc sec x, arcsecsec. Для данного значения предоставьте выражение (Пример 10), которое представляет все значения для каждой из этих функций. 13. Нарисуйте график функции

Болезнь 1 tg- »ctg ^> sec7 ‘cosec ^ r- 14. Указывает, что cos * и sin x не являются рациональными функциями l:. [Функция вызывается периодически с периодом a if / (x) = f (x — \ — a) для всех значений x, для которых определено f (x). Следовательно, период cos x и sin x равен 2 годам. Если периодическая функция не постоянна, она не может быть рациональным числом. Конечно, PX) Q (x) ‘ Где P и Q — многочлены, и / (x) = / (q + a), и каждое из этих уравнений применимо ко всем значениям x. Пусть f (0) = k.

Тогда уравнение P (q) -kQ (x) = 0 удовлетворяется бесконечным числом значений q, то есть x = 0, o, 2a и т. Д., И, следовательно, всеми значениями x. Следовательно, f (x) для всех x, то есть f (g) является константой. } 15. Обобщите предыдущий результат, чтобы показать, что периодическая функция не может быть алгебраической функцией от x. (Уравнение, определяющее алгебраическую функцию ym + Ryrn-i_j_ …- {- Rm = 0, (1) Где Rit … y Rm — рациональная функция от x. Это уравнение PoT + P1Ut ~ 1 + … = 0, Где P0, я „…” Pm — многочлен от q. Вывод, как в предыдущем примере, pjtm + p ^ m-1_ | _ … + Pm = Q Для всех значений х.

В результате y ^ = k удовлетворяет уравнению (1) для всех значений q, и одна система значений алгебраических функций является постоянной. Разделите (1) на y-k и повторите аргумент. Наконец, мы заключаем, что алгебраическая функция состоит из одной и той же системы значений k, k \ …, то есть нескольких констант, для любого значения q. 16. Обратный синус и обратный косинус не являются ни рациональными, ни алгебраическими функциями. [Это вытекает из того факта, что дуги sin.с и дуги cosх имеют бесконечно много значений для значений х между –1 «и — {- I.]

Трансцендентальные функции других классов. Следующими наиболее важными тригонометрическими функциями являются экспоненциальная и логарифмическая функции, которые рассматриваются в разд. На данный момент эти функции еще не доступны. Большинство других классов трансцендентных функций, таких как эллиптические функции, функции Бесселя, функции Лежандра и гамма-функции, полностью выходят за рамки этой книги.

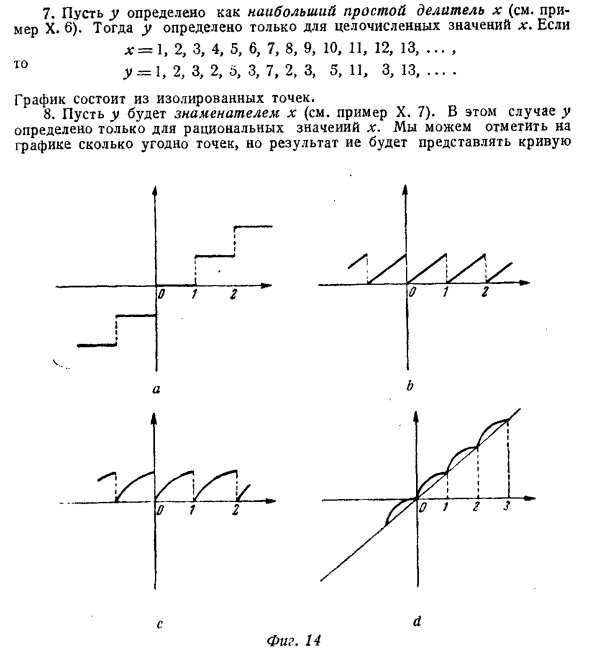
Однако, хотя теоретический интерес гораздо меньше, чем рациональных, алгебраических и тригонометрических функций, существуют некоторые основные функции, которые особенно полезны в качестве примеров возможного разнообразия зависимостей функций. Пример XVI. 1. Допустим, у — [*). Здесь [x] представляет наибольшее целое число, меньшее или равное x. График показан на фиг. 14а. Левый конец сплошного сегмента принадлежит графу, а правый конец не принадлежит. 2. у = х- [х \ (рис. 14б). Z.u = Vx-Y ~ (рис. 14в). 4. Y = [x] + Y x- [x] (рисунок III). 5. y = (x- [x)) \ [x] + (x- [x) Y. 6.y ^ lVx], [x *], Vx-iVx), W-x *).

Определите y как наибольшее простое число x (см. Пример X. 6). Тогда у определяется только для целочисленных значений х. если LG = 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, …, тогда y = 1, 2, 3, 2, 5, 3, 7, 2, 3, 5, 11, 3, 13 ….. График состоит из изолированных точек. 8. Пусть у — знаменатель х (см. Пример X. 7). В этом случае у определяется только для рационального значения х. Вы можете отметить на графике столько точек, сколько хотите, но результат представляет собой кривую О 1 О 1 d и Та же фигура. 14

В обычном смысле слова. На графике есть точки, которые соответствуют иррациональным значениям x. Нарисуйте линию, соединяющую точки (N — 1, N) и (iV, N). Где N — положительное целое число Указывает, что число точек графа в этом сегменте равно количеству натуральных чисел, меньших, чем N, и относительно простое для N. 9. Если x — целое число, .y = 0, если x — нецелое число, y = x. График берется из линии y = x путем удаления точек. …, (-1, -1), (0, 0), (1, 1), (2, 2), … Добавить n очков …, (-1,0), (0, 0), (1, 0), (2, 0), … ОСЬ LG-OV.