Оглавление:

















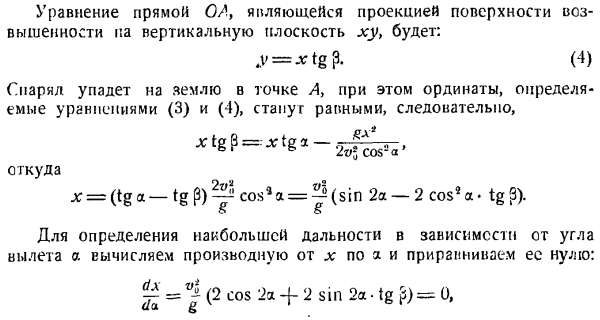












Траектория и уравнения движения точки
- Уравнение движения для локуса и точек 1°.Основные понятия. Траекторией точки называется линия, описываемая точкой движения в пространстве. Траектории могут быть плоскими или пространственными кривыми. Движение точки определяется установлением закона движения. Закон движения точек (уравнения) устанавливает зависимость расположения точек во временном пространстве.
Движение точки M в фиксированной системе координат xyz определяется установкой 3 функций (рис.3.1). * = / > ( ’). J’ = / *(<). r = / 3(0, (1 *) Присвойте уравнению (1*) значение времени t = ti для определения координат Задача 3.2. На кривошипе длина a перпендикулярна плоскости фигуры и вращается вокруг оси через точку O. угол<p между неподвижной осью Ox и кривошипом изменяется пропорционально времени. = КТ.
Это называется уравнением движения точки. Людмила Фирмаль
Создайте уравнение движения для точки N в декартовой системе координат. Найдите уравнение его орбиты. Определяет полный 1-кратный поворот точки N и точку, в которой координаты обеих точек равны. The solution. To составьте уравнение движения точки N, необходимо представить ее координаты в виде функции времени. Из рисунка найдите координату x в точке N. Х = О с COS <Р、 y = на грех cf Или х = а соѕ kty у = грех КТ. (И (2)
Это будет искомое уравнение движения для точки N. Чтобы найти уравнение орбиты точки в явном виде, необходимо исключить время из уравнения motion. To сделайте это, квадрат каждого уравнения движения. x1 = A1 cos2 kt, y * = ar sin * kt、 (3) (4) Добавьте уравнения(3) и(4). х * + г * = в \ Это уравнение траектории точки N определяет окружность с радиусом вокруг начала координат.
- Определим время полного 1 поворота точки N. это время, когда происходит угол c. Оно изменяется на 2Т. Радиан.: 9 = кт = 2К、} Откуда? Найти начальное положение перемещения point. To для этого нужно подставить значения уравнений движения (1) и (2)£= 0. — v0 = a, y o = 0. Определяет точку, в которой обе координаты точки N равны друг другу. Х = Y = а соѕ КТИ = а ktif грех Иначе говоря Кей-Ти тг = 1. Это равенство возможно «1 + 5-,(5) Где я= 0、1、2、3、…
Из (5)определяется, когда координаты точек равны 。 — К. ти = = КН + РК- Задача 3.3.In в предыдущей задаче, если угол<p равен kt + P, то k и p являются постоянными величинами и определяют движение точки A4, являющейся проекцией точки N на ось Ax. Решение. Поскольку точка M движется линейно вдоль оси Ox, ее движение определяется уравнением 1. х = о соз СР = е соз(т + п).
Это уравнение линейного гармонического колебательного движения. Людмила Фирмаль
Затем по координатам определяется максимальное отклонение точки м от центра колебаний О. МПМ = а ХІ =-а. Величина a называется амплитудой колебаний, kt — (- (J называется фазой колебаний, ap-начальной фазой колебаний. Определите период колебаний, то есть время, в течение которого точки совершают 1 полное колебание, то есть возвращаются в исходное положение с той же скоростью и величиной. Обозначим период буквой Т и найдем его значение из условия, что приращение фазы колебаний за это время равно 2π. Иначе говоря
Задача 3.4.Точки перемещаются в соответствии с уравнением. x = A cos(kt-e), (1) г = Б, потому что КТ(2) Определите уравнение траектории движения точки. Как изменяется локус точек при увеличении разности фаз£от 0 до 2r? The solution. To найдя уравнение орбиты точки в явном виде, нужно исключить время из уравнения motion. To для этого сначала преобразуем уравнение движения. х = а соѕ(т-е)= а [потому что КТ потому что£-(- КТ грех грех ЭЖ.(3) решая уравнения (2) и (3) для cos kt и sin kt, получим: Х г — г соз£ а б. Преступление. потому что КТ =£о грех КТ = Добавьте эти уравнения, возведя их в квадрат. г, (т -£»»’) ’ 1 Б% ’ °1 (4) Sin2 е
Или в конце: — В + М — ^^ ко ^ грех ’、 уравнение (4) для любого значения e является уравнением эллипса. Из этого уравнения максимальные и минимальные значения являются Параметры±соответственно. a для x и zt b для y. таким образом, во всех случаях эллипс вписывается в прямоугольники со сторонами 2a и 2b. измените значение от 0 до 2ir. если e = 0, то выражение(4) принимает вид:
Так, если фазы обеих составляющих колебаний перпендикулярны друг другу, то эллипс вырождается в 2 совпадающие прямые, являющиеся диагоналями прямоугольника(рис.<). если е увеличить от 0 до ir / 2, то на 1 ее оси будет постепенно расширяться эллипс, направление которого совпадает с диагональю прямоугольника (рис.6). для e = it / 2 выражение(4)принимает вид)
То есть, эллиптическое уравнение принимает каноническую форму. при дальнейшем увеличении s овалы снова сужаются в своих отверстиях(рис. D), а при e = m вырождаются в другую диагональ прямоугольника (рис. E). в этом случае уравнение (4)принимает вид: Далее, если увеличить s от, процесс повторяется и становится зеркальным отражением первой половины процесса (рисунок E, EHU h). Как и в анализируемом примере, частоты обоих колебаний перпендикулярны друг другу
’/ х * я \ Дж — *- Я-В К задаче 3.5. В зависимости от изменения n т. е функционирует через этапы декомпозиции, описанные выше. Задача 3.5.Игнорируя сопротивление воздуха, точка м, брошенная под углом а относительно горизонта, движется согласно уравнению. 0) (2) О г = v0 в грехе л-т- В этих уравнениях v0, a, g являются фиксированной величиной.
Определите уравнение траектории движения точки, максимальную высоту подъема от уровня начального положения h, горизонтальное расстояние, до которого точка достигает наивысшего положения s, и горизонтальное расстояние точки. The solution. To определив уравнение орбиты точки в явном виде, необходимо исключить время из уравнения движения. Получаем из первого уравнения Т = — (3) х = вентиляционно-перфузионное потому что•Т、 гт. *
Подставляя это уравнение в уравнение(2), Находим орбитальное уравнение, представляющее интерес. г = ТГА-х- (4) л. » 2v’I cos2 a Из аналитической геометрии известно, что это уравнение параболы с осью симметрии, параллельной оси y axis. In дело в том, что каждому значению y соответствует 2 значения x. так как значения координат η== 0 и y = 0 удовлетворяют уравнению, то эта парабола проходит через начало координат.
Чтобы определить максимальный уровень точки A, нужно найти экстремум y по правилам дифференциала calculus. To для этого вычислите производную y относительно координаты x、 d v dv dt dx L-это то же самое, что и ее пуля. Потому что это может быть ограничено Равна производной пули У = / F = в Синоу-накопителей =0.(5) Таким образом, y достигает следующего экстремума. =(6)
Подставляя значение этого времени в Формулу(2), Находим максимальную поднятую высоту. , _ vl грех * в г. *!Я * в 1 г%sin2 д ~~ Uth-g 2GT—2-g ’ этот экстремум y на самом деле является максимумом, а не минимумом, потому что 2-я производная y при t = t1 отрицательна. П \ ш,= — с- Для определения абсциссы s, в которой точка достигает наивысшего положения, необходимо подставить в Формулу (1) значение времени, соответствующее этому моменту (6). во грех а вл грех 21 5 = г, = р> в коса -> -= учитывая it_y = 0, горизонтальная дальность полета I определяется из орбитального уравнения (4).
log A x cos2 a следовательно 2 значения x\ Т / л грех 2а х0 = 0, ХН = 1 = 8. Первое значение соответствует первому моменту (моменту отправления точки), А второе определяет горизонтальное расстояние. Сравнивая значения /и 5, можно сделать вывод, что/ = 2s, то есть точки достигают наивысшего положения в диапазоне горизонтальной половины. Итак, положение точки в пространстве в этой точке.
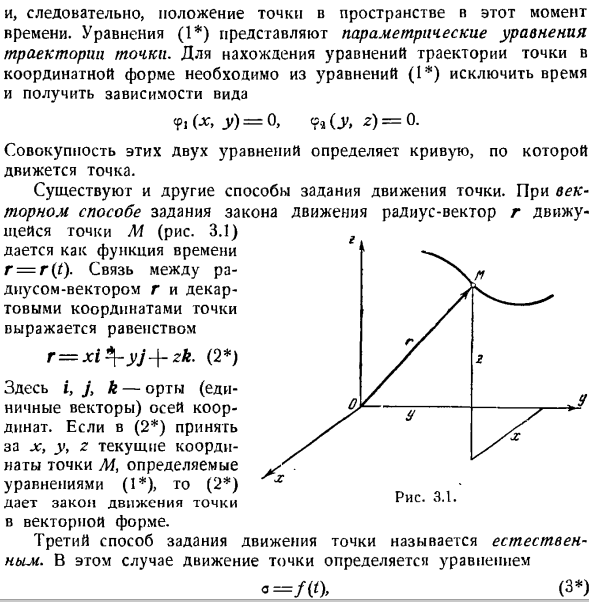
Уравнение (1) представляет собой параметрическое уравнение траектории a point. To найдя уравнение орбиты точки в координатной форме, нужно исключить время из уравнения(1) и получить форму зависимости. БФ,(Ци, г)= 0, 9а, КР, з)= 0. Комбинация этих 2 уравнений определяет кривую, по которой перемещаются точки. Есть и другие способы указать движение points. In векторным методом, определяющим законы движения, радиус-вектор r движущейся точки M (рис.3.1) задается как функция времени r = r (t).Связь между радиус-вектором r и Декартовыми координатами точки представлена уравнением Р = ХІ * \ — ый + ЗК. (2 ) Где i, j и k-единичные векторы (единичные векторы) осей. (2)
Если вы получаете x, y> z, текущие координаты точки A4, как определено y. уравнение(1), то (2) x Дайте закон движения точек в векторной форме. 3-й способ задания движения точек называется natural. In в этом случае движение точек определяется уравнением а = /(<), (3 ) Обратите внимание, что вы можете найти нужный диапазон и высоту, не прибегая к differentiation.
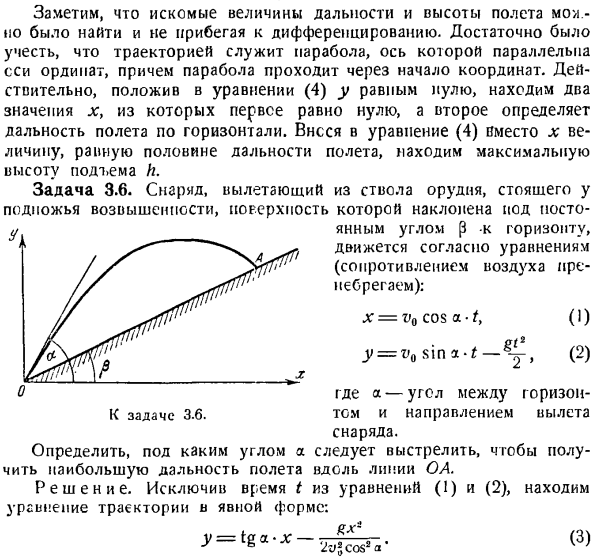
It достаточно было учесть, что орбита представляет собой параболу, параллельную продольной координатной оси, а парабола проходит через origin. In дело в том, что если в выражении (4) y установить его равным нулю, то получится 2 значения x. первое значение равно нулю, а второе определяет дальность горизонтального полета. Если вместо x в уравнении (4) ввести значение, равное половине дальности полета, то получится максимальная высота подъема I. Задача 3.6.Снаряд, вылетающий из ствола пушки, стоящей у подножия холма, наклоняется на определенный угол Р йода относительно поверхности горизонта и движется согласно уравнению(игнорируя сопротивление воздуха). x = v0cosa•(1) O ’ где A-горизонтальный угол 3.6 для.
Объем и направление отправления Оболочка. Определите, под каким углом нужно вести огонь, чтобы получить наибольшую дальность полета по линии ОА. Решение. Если вы исключите уравнение (I) и время t из (2), вы найдете явную форму орбитального уравнения. г = ТГА-ЛГ -.. UL(3) Откуда? ctg2a = — ТГП、 Или 9а — — — й-3-2 и г」 Таким образом, максимальным диапазоном будет угол броска, равный половине угла между вертикалью(отрицательной осью y)и градиентом OA. Задача 3.7.Точки, которые брошены наискось относительно горизонта, движутся в воздухе. Его сопротивление пропорционально скорости, согласно формуле. Г = ФК〜( ь я н «+ я)(1-е -*») — Ж.(2) В этих уравнениях v0t, a, k, g являются положительными константами.
И после простой трансформации — Injl — ^ — х). (4) kg \ V0 COS <1)4 ′ Подставим (3) и (4) в выражение(2), чтобы получить выражение траектории точки в явном виде. _ kv0 грех о + 1 1/1 _ _ х \ Ъ-КН. с ^ Я Х \ в. потому что в НД koQC () S3 1 k2g \ VQ COS i Чтобы определить максимальную высоту h от начального положения уровня, необходимо найти максимальное значение величины y, которое рассматривается как функция x-coordinate.
To для этого нужно вычислить 1-ю производную, согласно правилам дифференциального исчисления Т ды ды ДТ ДХ. Л. Динат x и сделать его равным нулю. ^ = ^ — И-φ、 Вы можете ограничить производную координаты y равным нулю по времени. Значение независимой переменной-время tx, найденное из этого уравнения, подставляется в уравнение(2). найдено максимальное или минимальное значение Y. Если 2-я производная от y отрицательна в этой точке, то экстремум найденного y является максимумом, а противоположный случай-минимумом. Используйте уравнение(2) для вычисления производной y по времени, равной нулю. p =(v0 sin a + l-1 = 0.
И затем… е〜4ч-1. koQ sin a-f 1 ′ или интернет = ^ ьп(* х / 0sina4-л). Если подставить эти значения в Формулу(2), то после простого преобразования найдем экстремальные значения 。 вентиляционно-перфузионное грех 1. 。 。В первой половине года. Угол = h -lln (kvQ Sin a + l). Вычислите производную 2-го порядка от y, чтобы убедиться, что найденное значение действительно является самым большим Р =-кг (v0 в Си н а 4-е ЖЖ-КГТ. поскольку ky g, r / 0 является положительным числом, а угол a находится в Q1, производная 2-го порядка отрицательна. Кроме того, определите, какая абсцисса точки достигнет наибольшей position.
To для этого достаточно подставить значение времени th, которое соответствует наивысшему положению точки в Формуле (1).Тогда у нас есть: _ PtfCOSaЛ _ 1 _ _ _ v%sin2a кг \ kv0 Sin в-Ф-1 г(kv0 грех, а-j-я)* Можно использовать уравнение траектории точки (5) для получения уравнения, определяющего горизонтальную дальность полета. Если положить координату y = 0 в уравнение (5), то 1 из значений X удовлетворяет трансцендентному уравнению грех + ’1 в F 1-х)= — о,(6)
И так далее. гг, с ФТ я ба-л ы г ы м я в Т / 0COSa 1 кг \ качеству звука, потому что буква » и Джей Си!== 0; это значение соответствует началу эстрального периода от начала координат в первый момент.2-е значение xb, являющееся корнем формулы (6), определяет горизонтальный диапазон. Это значение можно получить следующими способами Решение уравнения(6). для этого необходимо построить функцию для известных чисел с коэффициентами kt g, v0, q F(х)= Фет / У от греха-Ф- \
По качеству звука потому что — — — Х * В, Дж, потому что Дж т. к. Постройте значения x вдоль горизонтальной оси и постройте соответствующие значения f / x на вертикальной оси. Точка пересечения этой кривой и оси абсцисс дает 2-й корень формулы (b), то есть горизонтальную дальность полета. 2°.Переход от уравнения движения в декартовых координатах к естественному уравнению движения.
Если уравнение движения точки задано в декартовых координатах (Я) Х-ФЛ(т) и V = ф(т), з = ФЗ(0 Если вы хотите найти уравнение движения естественным путем, то вам нужно сначала определить траекторию движения точки, а затем найти законы движения этой точки вдоль траектории. Уравнение точечной орбиты получается путем удаления времени из уравнения движения (1). чтобы найти закон движения a = / ( / ), необходимо воспользоваться известной формулой для дифференциала Дуг. ±д ^ ДС = г (файлы DXF +(dyf-ф(у dzy — = МФ * ( * )+/; ’(Т)+ / 3 \ Ф.) ДТ(2 *)
При интеграции вы увидите следующее: а =±j в ВФ *(0(1Ф)+ / г(0 ДТ + С.(3 ) Любая интегральная константа C выводится из начального условия. Например, если трек начинается с начальной позиции точки, то f = 0 = салат ромэн.) (2) Подсчитав расстояние от первой позиции, определите уравнение траектории движения точки и ее законы. The solution. To получаем уравнение траектории движения точки, находим его из уравнения(1) потому что * =£(3) Подставим уравнение (2) в уравнение (3).
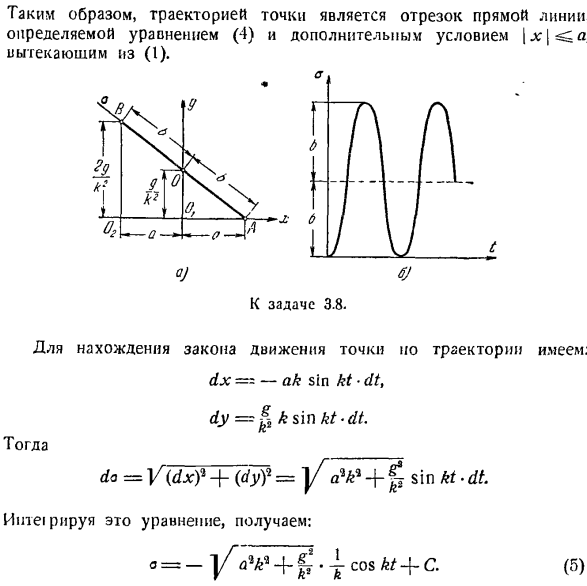
Итак, траектория точки представляет собой отрезок прямой, который определяется дополнительными условиями, вытекающими из формул(4) и (1). К задаче 3.8. Чтобы найти законы движения локуса точек wo, можно сделать следующее: ДХ — АК греха КТ * ДТ、 4Г =&к греху КТ-ДТ. После этого、_ у = в (ДХ) ’+(Д-Г?= Y aW + sin kt * dt. By уравновешивая это уравнение, оно выглядит так: Поскольку, согласно условиям задачи, координаты a вычисляются из начального положения точки,
Если/ = 0 a = 0, то подставляя эти значения в (5), получаем: 0 = _iAw + гл + с、 Откуда? С-Я / .Ш + Ф. Введите значение любой найденной константы C в формулу (5), и вы увидите закон движения точки по траектории. а = 1 + Ф3 — (я-потому что ЛО. Это уравнение гармонического колебательного движения точки.
По качеству звука потому что — — — Х * В, Дж, потому что Дж т. к. Постройте значения x вдоль горизонтальной оси и постройте соответствующие значения f / x на вертикальной оси. Точка пересечения этой кривой и оси абсцисс дает 2-й корень формулы (b), то есть горизонтальную дальность полета. 2°.Переход от уравнения движения в декартовых координатах к естественному уравнению движения. Если уравнение движения точки задано в декартовых координатах (Я) Х-ФЛ(т) и V = ф(т), з = ФЗ(0
Если вы хотите найти уравнение движения естественным путем, то вам нужно сначала определить траекторию движения точки, а затем найти законы движения этой точки вдоль траектории. Уравнение точечной орбиты получается путем удаления времени из уравнения движения (1). чтобы найти закон движения a = / ( / ), необходимо воспользоваться известной формулой для дифференциала Дуг. ±д ^ ДС = г (файлы DXF +(dyf-ф(у dzy — = МФ * ( * )+/; ’(Т)+ / 3 \ Ф.) ДТ(2 *)
При интеграции вы увидите следующее: а =±j в ВФ *(0(1Ф)+ / г(0 ДТ + С.(3 ) Любая интегральная константа C выводится из начального условия. Например, если трек начинается с начальной позиции точки, то f = 0 = салат ромэн.) (2) Подсчитав расстояние от первой позиции, определите уравнение траектории движения точки и ее законы. The solution. To получаем уравнение траектории движения точки, находим его из уравнения(1) потому что * =£(3) Подставим уравнение (2) в уравнение (3).
Итак, траектория точки представляет собой отрезок прямой, который определяется дополнительными условиями, вытекающими из формул(4) и (1). К задаче 3.8. Чтобы найти законы движения локуса точек wo, можно сделать следующее: ДХ — АК греха КТ * ДТ、 4Г =&к греху КТ-ДТ. После этого、_ у = в (ДХ) ’+(Д-Г?= Y aW + sin kt * dt. By уравновешивая это уравнение, оно выглядит так: Поскольку, согласно условиям задачи, координаты a вычисляются из начального положения точки,
Если/ = 0 a = 0, то подставляя эти значения в (5), получаем: 0 = _iAw + гл + с、 Откуда? С-Я / .Ш + Ф. Введите значение любой найденной константы C в формулу (5), и вы увидите закон движения точки по траектории. а = 1 + Ф3 — (я-потому что ЛО. Это уравнение гармонического колебательного движения точки.
Где A-криволинейная координата, измеренная вдоль дуги от некоторой начальной точки O на орбите (рис. 3.2).С помощью этого метода траектория движущейся точки является K и M известны. Криволинейная координата — это длина начальной односторонней дуги Дело в том, что и、 Другой-отрицательный (нужно указать направление положительной ссылки).
Уравнение (3) называется естественным уравнением движения. В естественном способе установки движения, есть также 3 уравнения. Первое уравнение-это точка ((3), 2 Рисунок 3.2. Точка O (центр вибрации), в которой происходит вибрация, является расстоянием 。Амплитуда колебаний от исходного положения В момент времени t = 0, находится в крайних точках l. время t = R. in j2k, при COS KT = 0, точка находится в центре колебаний O. In время t = njk, потому что кт — 1, точка находится во 2-м крайнем положении точки B. Графически движение точек показано на рисунке.。
Строится фигура и траектория движения лба. На рисунке b показана зависимость j или времени Задача 3.9.Точка M перемещается по следующему уравнению: х = соѕ кт, (1) у = грех кт, (2) з = БТ, (3) Где а, к и B-константы. Путем подсчета расстояния от начального положения точки. Определите уравнение локуса точек и закон движения точек вдоль локуса The solution. To определите уравнение траектории движения точки, найдите время из уравнения(3)и добавьте это значение к (1) и(2).И затем… к К задаче 3.9. Х =О.
Потому что в Z、 г = грех по Г по З. Это спиральное уравнение. Из уравнений (1), (2) видно, что проекция точки на плоскость xy представляет собой круг времени 2njk. За это время, проекция точки на ось Z будет двигаться следующим образом в 2р ч Икс’ Это называется винтовой шаг. На поверхность цилиндра радиуса а намотана спираль. Найдите следующее, чтобы найти закон движения точки вдоль траектории. ДХ—а / г грех КТ•ДТ, ды =-Ак, потому что КТ•ДТ, ДЗ == БДТ.
Затем дуга стала следующей. DY = в (дх) ° —(dyf (dzf = / / дт. Когда вы консолидируете это equality. It выглядит так 0 = 1 / aW + Pt + C(4) Для определения произвольной интегральной константы используйте начальное условие. t = 0, o = 0, потому что arccant начинается в то же время, что и time cant. Если подставить эти начальные условия в Формулу(4), то найдем: 0 = 0 — / / — С. Итак закон движения точки по спирали、
Если вы хотите считать положительные значения-против часовой стрелки. Движение происходит против часовой стрелки по спирали: точка x0 = м, Дж / 0 = 0, 20=.It начинается с 0. Овладеть навыками решения задач, редактирования и изучения уравнения движения, а также определения траекторий движения точек, И. В.。Мещерский, из издания»сборник задач теоретической механики» с 1950 года рекомендует решать следующие задачи: 3д、312、314、 315、317、318、320、321。
Поскольку кривая в пространстве представлена уравнением 2 поверхностей, то остальные уравнения определяют траекторию движения точки. Это траектория точки. Среди других систем координат, используемых при исследовании motion. In в полярной системе координат (рис. 3.3) положение точки в плоскости определяется длиной отрезка прямой, соединяющего радиус p-неподвижный центр O и точку перемещения M, и углом между неподвижной линией Ox, (полярной осью) и отрезком OM
. In в этом случае уравнение плоского движения точки M Рисунок 3.3. (4 ) Я буду.: Р = P(т),<р = < \ >(). Сферические и цилиндрические координаты часто используются для изучения движения точки в пространстве. Сферическими координатами точки M (рис.3.4) являются расстояние r точки M от неподвижного центра O, угол φ (угол поворота плоскости zOM относительно неподвижной плоскости xOz) и угол ? =?(’) * (5 *)
Уравнение движения для цилиндрических координат: р = п(о> т = м р = РЗ). (си *) м г Так… 1. Рисунок 3.4. Да. Чтобы перейти от сферических координат к декартовым, используйте следующую формулу:> х = р с с COS <Р соз ф, г-т с с COS <Р грехом Ф, З = Р грех <п.
Формула для перехода от цилиндрических координат к ортогональным декартовым координатам: х = р соз Ф, У = р грехом Ф, з = з В отличие от декартовых, сферических и цилиндрических систем координат, они называются криволинейными системами координат. Уравнение движения точки может быть представлено графически. Если независимая переменная t (время) строится по абсциссе, а координаты движущейся точки-по ординате, то на графике получается кривая зависимости координаты от времени, то есть уравнение движения.
Такой график должен быть составлен для каждой из 3-х координат, определяющих движение точки в пространстве. График движения является、(3 *)、(4 *)、или вы также можете построить его, установив закон движения по-другому. Уравнение движения точки может быть приведено в виде таблицы, в которой каждому значению координаты соответствует каждое дискретное значение во времени.
Решение задачи определения законов движения и уравнения орбиты осуществляется в следующем порядке: 1) выбирается фиксированная система координат-прямоугольная, Полярная или другая; 1 или другая система с источником выбирается исходя из условий задачи, поэтому дальнейшее решение является максимально простым. 2) на основе условия задачи выбранной системы координат составляется уравнение движения точек. То есть найдена временная зависимость координат точки. 3) уравнение движения точки позволяет определить ее положение в любой момент времени, установить направление ее движения, найти траекторию и ответить на различные вопросы о движении точки.
Задача 3.1.Точка M совершает плоское движение в соответствии с уравнением. * = 6 — {3 т(я) г = 4Т. (2) Определите траекторию движения точки M. Решение. Найдите орбитальное уравнение в координатной форме, удалив время из обоих уравнений движения. Из 2-го уравнения получаем t = yj4.Подставляя это значение в первое уравнение движения, получаем уравнение орбиты ДГ = 6 + 0.7 бу. Это уравнение прямой линии. Примечание y = 0, jc = 6, x = 0, y = −8 для создания этой строки.
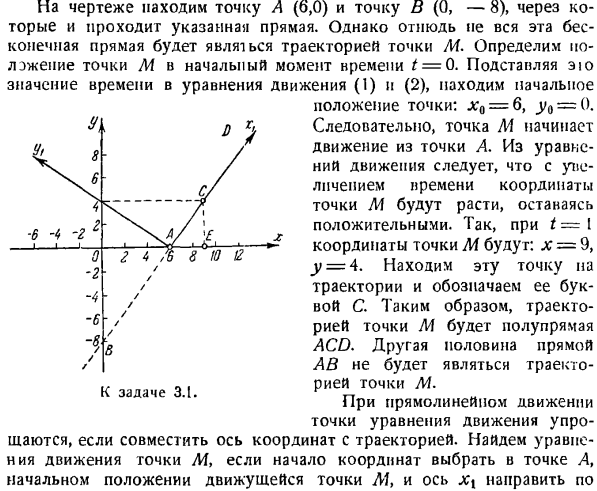
На чертеже найдите точки A (6.0) и B (0, −8), через которые проходит указанная линия. Однако не вся эта бесконечная прямая будет представлять собой траекторию движения точки М. определите местоположение точки М в начальный момент времени t = 0.Это значение времени подставляется в уравнения движения (1) и (2)、 Положение точки: xQ = 6, j / 0 =().Таким образом, точка М начинает двигаться из точки А.
из уравнения движения, с увеличением времени, координаты точки М становятся положительными и растут. Если ’ hack, t = I, то координаты точки M будут: x = 9, y =4.Найдите эту точку на траектории и обозначьте ее буквой C. Таким образом, локус точки M будет представлять собой полустрочку ACD. Другая половина линии AB не является траекторией точки M.
В линейном движении точки уравнений движения упрощаются, когда координатные оси объединяются с локусом. Найти уравнение движения для точки MU, если начало координат выбрано в точке A, а в начальном положении движущейся точки L1 ось xx направлена в следующем направлении. Y, 4, 8. — И/ ■ 6 1 1 ■ ■ g * 0 −2-4 g^, b / ✓ / / / 8 10 12 6 я J / / / в г. /
К задаче 3.1. Оси полуосей ACDy и yv перпендикулярны ей. Затем, из треугольника ace, используйте уравнение движения (1), (2) и узнайте ниже. x] =(x-6) ’ + Y = 9+ 1 B t2 = 251 \ Следовательно、 Си = ±51.(3) Знак минус (3) должен быть отброшен, так как точка M движется в положительном направлении xif axis. So, уравнение движения для точки M в новой системе координат выглядит следующим образом: = бу уу = 0. Для линейного движения точки, по существу, мы получили 1 уравнение движения. — 1 0 О! \, Икс Отправьте свое сообщение этому поставщику Задание 3.2-3.3.
Смотрите также:
Предмет теоретическая механика
| Произвольная пространственная система сил | Скорость и ускорение точки |
| Центр тяжести | Вращение твердого тела вокруг неподвижной оси |

