Оглавление:
Траектории, скорости и ускорения точек вращающегося твердого тела
Так как при вращении твердого тела вокруг неподвижной оси расстояние каждой из его точек до оси вращения должно оставаться неизменным, то очевидно, что все его точки описывают в этом движении окружности, плоскости которых перпендикулярны к оси вращения. Центры этих окружностей лежат на оси вращения и радиус каждой из них равен расстоянию соответствующей точки тела до оси вращения.
Очевидно, что радиусы всех этих окружностей поворачиваются за один и тот же промежуток времени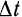 
на один и тот же угол 
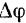, равный приращению угла 
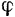поворота тела за этот промежуток времени, но точки, лежащие на разных расстояниях от оси вращения (точки 
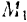и 
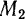на рис. 118), опишут при этом дуги различной длины.
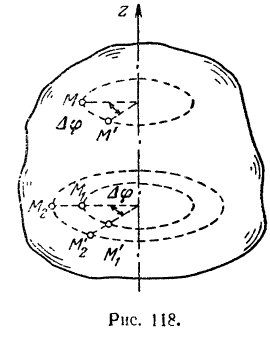
Зная угловую скорость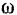 
тела и расстояние 
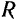какой-нибудь точки 
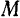тела от оси вращения, легко найти и скорость 
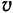этой точки.
Пусть за промежуток времени 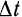, соответствующий приращению 
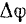угла поворота угла, данная точка перемешается из положения 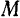в положение 
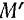(рис. 118).
Длина дуги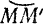 
, пройденной точкой 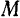по ее траектории, равна приращению 
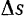дуговой координаты 
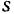этой точки.
Алгебраическое значение скорости точки, как известно, равно производной от ее луговой координаты по времени
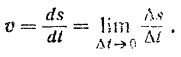
Но длина дуги окружности равна ее радиусу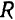 
, умноженному на соответствующий центральный угол в радианах, т. е. 
.
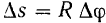Подставляя значение 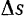в предыдущее равенство, получаем:
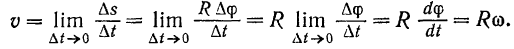
Алгебраическое значение скорости точки вращающегося тела равно произведению угловой скорости тела на расстояние данной точки от оси вращения
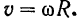
Направлен вектор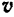 
скорости точки по касательной к траектории точки в сторону вращения тела. Иными словами, этот вектор перпендикулярен к радиусу, соединяющему ось вращения с рассматриваемой точкой. Из формулы (83) следует, что скорости точек вращающегося тела пропорциональны расстояниям этих точек от оси вращения.
Так как в формуле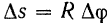 
приращение угла 
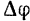должно быть обязательно выражено в радианах, то и угловая скорость в формуле (83) должна обязательно выражаться в рад/сек, рад/мин и т. д., но не в об/сек или в об/мин. Только в этом случае будет получаться принятая размерность скорости .
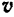При любом вращательном движении тела скорости 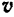его точек непременно изменяются (только по направлению при равномерном вращательном движении или и по направлению и по модулю при неравномерном вращательном движении), следовательно, точки вращающегося тела всегда движутся с некоторым ускорением.
Ускорение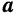 
точки вращающегося тела, как и ускорение всякого криволинейного движения точки, может быть разложено на касательное ускорение 
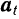часто называемое в этом случае вращательным ускорением, и нормальное ускорение 
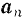называемое в этом случае центростремительным ускорением.
Полагая в формулах (68) и (69) для касательного и нормального ускорения точки 
и радиус кривизны 
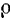траектории равным радиусу окружности, описываемой точкой, будем иметь:
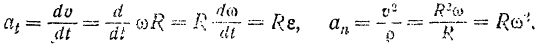
Величина вращательного ускорения тонки равна произведению углового ускорения тела на расстояние данной точки от оси вращения:
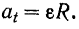
Модуль центростремительного ускорения точки равен квадрату угловой скорости тела, умноженному на расстояние данной точки от оси вращения:
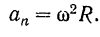
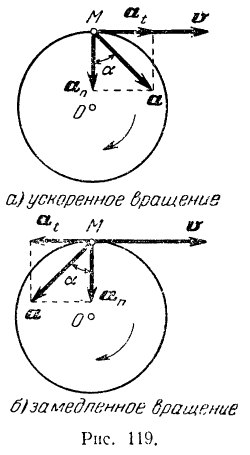
Направление вращательного ускорения точки совпадает с направлением ее скорости в случае ускоренного вращения тела (рис. 119, а) и направлено в сторону, противоположную скорости, в случае замедленного вращения (рис. 119, б).
Центростремительное ускорение точки всегда направлено к центру окружности, описываемой точкой.
Зная вращательную и центростремительную составляющие ускорения 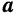точки, всегда можно найти величину и направление этого ускорения, изображаемого диагональю прямоугольника, построенного на векторах 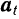и 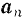(рис. 119).
Модуль этого ускорения
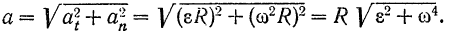
Острый угол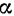 
между направлением ускорения 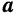точки и направлением радиуса (внутренней нормали к траектории) найдется из формулы
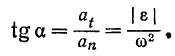
Для получения правильной размерности ускорени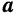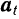й , и 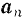в формулы (84), (85) нужно подставлять в
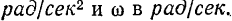
Пример задачи:
Шкив диаметром 600 мм вращается вокруг его оси. Скорость точек на его ободе равна в данный момент 1,5 м/сек.
Определить угловую скорость шкива в оборотах в минуту.
Решение:
По формуле (83)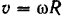 
вычисляем сначала угловую скорость 
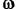шкива
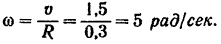
Пользуясь зависимостью (80)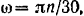 
, находим затем угловую скорость 
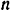шкива
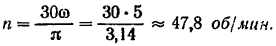
Пример задачи:
Маховик имеет в данный момент угловую скорость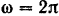 
рад/сек и угловое ускорение 
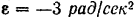. Найти скорость, вращательное, центростремительное и полное ускорения точки 
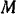маховика, находящейся на расстоянии 0,8 м от оси вращения.
Решение:
Скорость точки
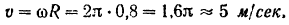
Вращательное ускорение точки
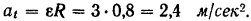
Так как знаки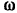 
и 
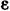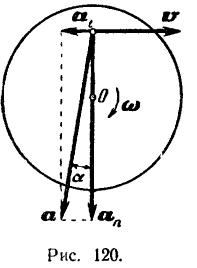
различны, то маховик вращается замедленно и потому ускорение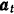 
точки направлено в сторону, противоположную ее скорости (рис. 120). Центростремительное ускорение точки
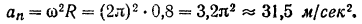
Полное ускорение точки
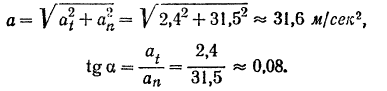
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
