Оглавление:










Точные решения дифференциальных уравнений
- За исключением фрикционной жары. Впервые теплоотдача в ламинарном потоке в трубах была рассмотрена теоретически Грацем*). Затем, независимо от него, решение этой проблемы снова Нуссельт. 2) Предоставляется и далее обрабатывается Гребером). В круглой трубе с радиусом R несжимаемая жидкость течет со средней скоростью W. Поскольку в потоке развиваются ламинарные характеристики течения, поле скоростей имеет вид Уравнение Хагена-Пуассона (уравнение (12) представлено ниже. Ось трубы является осью x в то же время. Его положительное направление совпадает с направлением тока. Расстояние по оси X В радиальном направлении радиус трубы обозначается R и g.
Такое распределение скоростей должно поддерживаться при теплопередаче conditions. In в этом случае вязкость (и Предполагается, что другие физические константы не зависят от температуры. Первоначально температурное поле жидкости является однородным, температура которого совпадает с температурой стенок. Начните с определенного участка (x = 0) и начните стенку трубы Последующее выполнение поддерживается при постоянной температуре выше или ниже температуры жидкости. Спросите, как меняется температура Сколько тепла обменивается стенка трубы с жидкостью на участке длины x = 1?
Абсолютно черных поверхностей не существует в природе, так как определенный процент падающего излучения всегда отражается, но существуют такие поверхности, которые отражают лишь очень малую часть падающего излучения. Людмила Фирмаль
Считывает температуру жидкости от температуры стенки 0 (x, g) (следовательно, & обозначает температуру жидкости, и в избытке или Незащищенный.) В случае стационарного уравнения энергии В цилиндрических координатах радиуса d ? (Где угол поворота равен В условиях ламинарного течения В этом случае, используя формулу (55), можно использовать обозначение te.
По соображениям симметрии, пусть dgMd ^ = 0.In кроме того, мы предполагаем, что dbb / dx мал по сравнению с dbb; dgr \this is Осевое распределение температуры krn-visa незначительно по сравнению с радиальной кривизной*).Физическое содержание этого предположения Она заключается в том, что теплопроводность среды в направлении течения будет равна zero. In другими словами, чистая теплопроводность направления потока равна По сравнению с ним гораздо важнее теплопередача за счет конвекции.
Где также с учетом распределения скоростей по уравнению (55), уравнение энергии Может быть представлен В зависимости от ситуации в регионе、 Oe-начальная температура жидкости перед нагревом или охлаждением секции(измеряется от температуры стенки). для решения дифференциального уравнения (57) функция O (x, r) Может быть представлен в виде произведения 2-х функций.1 зависит только от x, другой 1 зависит только от r. 。 по мере увеличения x температура жидкости должна постепенно приближаться к температуре стенки. Таким образом, естественно, Φ (χ) можно считать отрицательной экспоненциальной функцией. Например, следующая форма экспоненты 。 Для всех x> 0 и r = R, стенка трубы, следующая за 0 = 0.
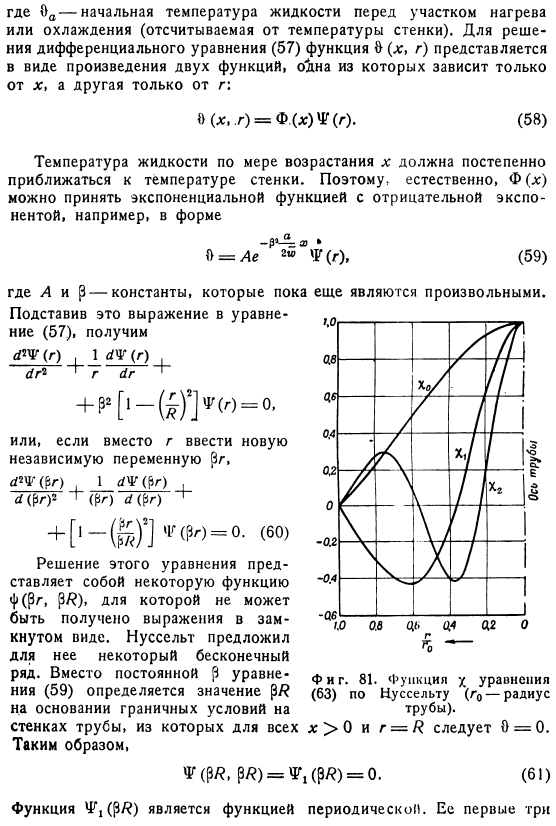
Функция 4f1 (PR) является периодической функцией. Ее первые 3 Нулевая точка определяется Нуссельтом в виде (Я ₽) o = 9o = 2.705 ® i = p, = 6.66 (0r), = 1 * 3 = 10.3 Вы можете ввести новую функцию, определив ее с помощью уравнения•/ _ Для данного 3 аргумента, уравнения строятся функции Хо, XI, и ХД. 81.To определите границу» константы а» 。 Теперь, решая уравнение (59), опираемся на конкретное решение Или обобщенный Если введен диаметр D = 2R. Поэтому относительное «изменение температуры», выраженное в соотношении начальной разности между температурой жидкости и температурой стенки, может быть выражено как функция 2-х измерений. Результаты вычитания Тоже фигура.
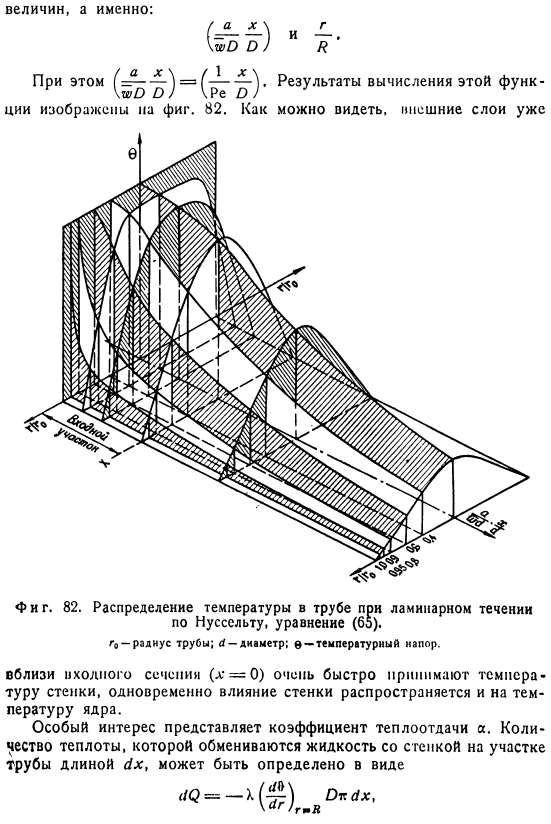
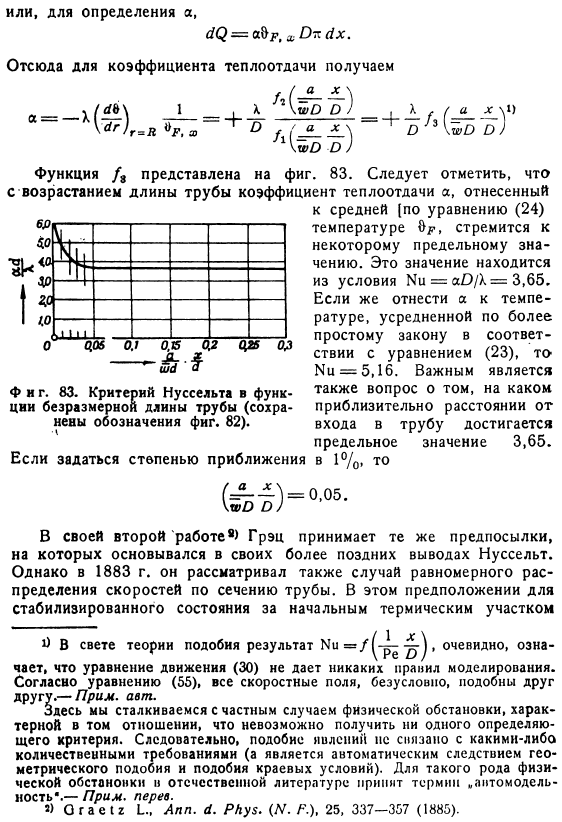
Вы можете видеть, и Вблизи входной секции (x = = 0) они сразу же совершают обход стены, в то время как температура ядра под воздействием стены распространяется. Особый интерес представляет коэффициент теплопередачи. Теплообмен между жидкостью и стенкой по длине трубы dx можно определить как: 。 Отсюда и коэффициент теплопередачи Тоже фигура. 83.Критерий нуссельта в функции безразмерной длины трубы (сохраняется Если задать степень приближения Существует также проблема достижения предела 3,65 на приблизительном расстоянии от входа до трубы. 。 Во 2-й работе*) Грац принимает ту же посылку, что и нусселт, основанную на последующих выводах.
Но в 1883 году он также рассматривал дело об униформе Распределение скоростей по сечению трубы. В этом предположении стабильное состояние за пределами начальной области теплоты > ) В свете теории подобия результат Nu yy) * однозначно означает, что уравнение движения(30)не дает планильного моделирования. Согласно формуле (56), все скоростные места、 Они, безусловно, похожи друг на друга.
Автор Здесь мы сталкиваемся с частным случаем физической ситуации, характерным в том смысле, что невозможно получить единое определение criterion. As в результате сходство явлений НС связан с количественными требованиями (это автоматический результат геометрического подобия и подобия граничных условий).Этот вид интенсивной окружающей среды В отечественной литературе принят термин»самоподобие». 。 Мы видим, что Nu = aD / X = 8.In это утверждение, корпус прекрасно справляется с проблемой нагрева или охлаждения цилиндра(стр. 77).、 Достаточно разделить обе стороны дифференциального уравнения температурного поля цилиндра на w = dxldt.
Решение в случае, когда температура стенки трубы изменяется по линейному закону, было дано Орлом и Фергюсоном*>’.В описании таких задач значительно меньше математических задач Это сложнее, чем рассмотренное решение Граца-нуссельта above. In факт, для устойчивого потока это предположение является Поток тепла через стенки трубы(это можно сделать, например, с помощью электрического нагрева); В этом случае решение дается на основе следующих предположений о форме температурного поля, в отличие от произведения уравнения (58).
Введение dy / dx-A в уравнение энергии (57) дает обыкновенное дифференциальное уравнение Кто решает Здесь мы использовали граничное условие 8 = 0 для r-R (потому что это разность температур между жидкостью и стенкой).Таким образом, градиент температуры вблизи стенки для всех x Определяется зависимостью Для среднего значения температуры по поперечному сечению получим значение w ® из Формулы (24), согласно формуле (55). Поэтому о критериях нуссельта, связанных с диаметром Тепловая нагрузка стенки с градиентом температуры а связана зависимостью Длину участка трубы можно также получить непосредственно из теплового баланса.
Дальнейшее решение ламинарного течения в канале связано с 9-й задачей о плоском зазоре. Ганеман и Эрет)) показали решение в случае, когда температура стенок с обеих сторон постоянна Теплообмен. Elser 2 > рассматривал случай теплопередачи только через 1 из стен, на которых противоположная стена изолирована. Янсен3) продлить эти решения в случае изменения Температура стенки по линейному закону. Краткое изложение этих результатов приведено в таблице. 13 *>.
- Другие случаи, которые Левеком расследовал 6); обзор работы Druve>также следует отметить. Ганеман. ) Определяли значение числа Nu в том случае, когда температура стенки после резкого изменения подчиняется линейному закону. Его значение находится между 3,65 И 4.36.Впоследствии мы рассмотрели случай охлаждения или нагрева стенок канала жидкостью, в котором коэффициент теплопередачи от наружной стенки остается неизменным. 8) постоянное значение.
Все описанные выше исследования ламинарного течения основаны на предположении о постоянстве физических constants. In кроме того, предполагалось, что теплота трения незначительна Small. In в ходе дальнейшего рассмотрения эти предположения будут отклонены 1 на 8) Критерий нуссельта предел ламинарного течения в канале Определяемый размер-это диаметр трубы или ширина зазора. Коэффициент теплопередачи связан со средней температурой жидкости[согласно уравнению (24)] «…Критерий Трубы круглого сечения 3.65 Грац(1883), нуссельт(1910) b. учитывая трение heat. In в этом случае нельзя игнорировать функцию диссипации в уравнении энергии (18).Прямой.
Поток энергии, проходящий через единицу площади поверхности раздела сред в единицу времени, генерируемый излучением, испускаемым средой 2, называется излучательной способностью и обозначается буквой е. Людмила Фирмаль
С появлением этой функции можно сделать вывод, что Выделение тепла трения происходит из-за большого градиента скорости, который может возникнуть даже при низкой абсолютной скорости, например. В зазоре подшипника скольжения. Этот вопрос рассматривался Vogelpole1).Процесс нагрева под действием трения, учитывающий зависимость вязкости от температуры ТКМ, исследовался по названию 2). В качестве примера точного решения дифференциальных уравнений с учетом теплоты трения рассмотрим устойчивое ламинарное течение в плоской щели. Этот расчет был дан Шлихтингом 。 Предполагалось, что движущаяся среда несжимаема, а физические константы не зависят от температуры.
При этих условиях, согласно уравнению(18), полное уравнение энергии стационарного плоского течения приобретает вид: 。 Направление потока. Направление y перпендикулярно st. Для стабильного течения возьмем dy / dx = 0 и b1b1dxg = 0, кроме того, во всем поле»1 ^ =0.«В то же время, производные dwxldx, dWy’dy и dwuldx также исчезают. И так оно и есть.、 Диссипативная функция выражения (18a)упрощается до выражения i) (dwa / dy)^. в результате тепловой поток, перпендикулярный направлению потока, должен быть уравновешен теплотой трения. Иметь Здесь мы пишем уравнение, принимая во внимание тот факт, что•u> xi = lw. Для скорости примите распределение Хагена-Пуазейля Где 2s-ширина зазора.
Если вы думаете о формуле (67) и (68) вместе、 Если температура стенки щели различна, то граничные условия в Формуле (69) принимают вид & = & для y= — s и 8 = = 82 для y = — j-s.
О распределении температуры Последний член определяет изменение температуры за счет теплоты трения, которая накладывается на явление теплопроводности ®.Тепловой поток стены мы просим от g = \(dn / dn).где n-Нормаль стенки, и является положительным значением > ) Средняя скорость w определяется по перепаду давления в направлении потока (dp / dx) по формуле w =- (dp / dx) s / 3i).Максимальная скорость по оси ВМО = ■ 1,5 «、 * ) при отсутствии теплоты трения от d59 / by2 = 0 получены незначительные решения в виде линейного изменения температуры между 9t и 9a. Не имею Рассматривается направление от стенки к жидкости.
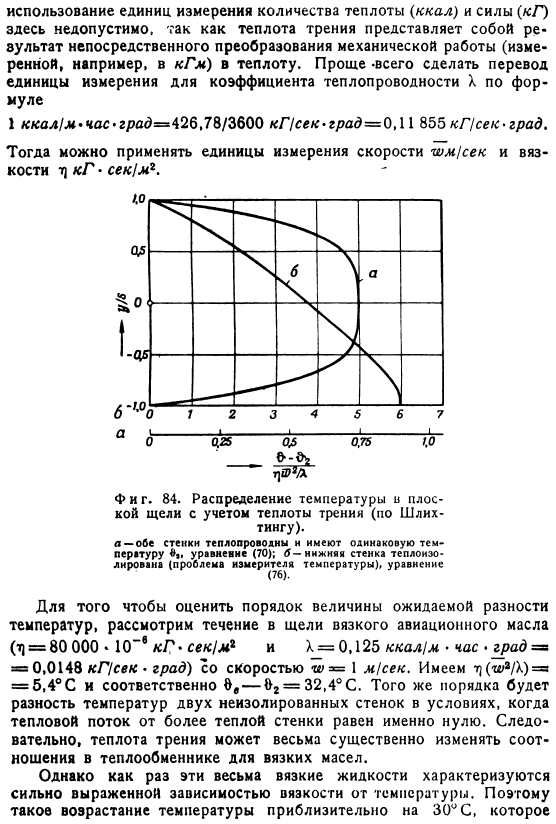
О нижней стенке 8= И Сверху=& & & 2 Общий тепловой поток через обе стенки равен Поток от теплой стенки (82) к холодной стенке (9.) теплый Может дать обратный эффект фрикционного тепла в стене высокой температуры (?2> 0) также отводить тепло. Этот эффект Происходить если q2 = 0, то приток тепла в нижнюю стенку qt в 2 раза больше. Если температура обеих стенок одинакова (01 = 82), то по формуле (70) распределение температуры устанавливается по параболе на 4 градуса. 84. Она представлена кривой а.
Максимальная температура на оси канала, независимо от ширины канала, определяется уравнением ( Граничное условие Если нижняя стенка изолирована, то дифференциальное уравнение (69) описывается уравнением dd / dy = 0 для y = — + $и y =-c. Формат решения таков Это распределение также показано на рисунке 4. 84 (кривая 6).Равновесная температура изолированной стены равна 8, что обычно называют ее собственной температурой. Этот. Температура выше температуры неизолированной стены В этом случае он также не зависит от ширины канала. Это выражение является новым безразмерным критерием, который может быть получен непосредственно из выражения (67).
В численных расчетах соединения являются Использование единиц измерения теплоты (ккал) и силы (кг) здесь не принято, так как теплота трения является результатом прямого преобразования Механическая работа в тепле (измеряется в КГМ, например). проще просто преобразовать единицу измерения коэффициента теплопроводности х по формуле 。 Затем можно использовать Тим / С и единицы измерения вязкости 1) кг с! мг. Тоже фигура.
Распределение температуры в плоской щели с учетом теплоты трения(по Шлиху Для оценки порядка величины ожидаемой разности температур рассмотрим расход зазора вязкого авиационного масла (t] = 80 000•10 » кг-сек / М1 и X = 0,125 ккал / м час• Град= = 0.0148 кг / с * Град) скорость U> = 1 м! Второй m] (o> 2 / k)= 5.4°C, следовательно, 8, −61 = 32.4°C. тот же размер будет иметь 2 разности температур, которые не изолированы Стена в состоянии, когда тепловой поток от теплой стены точно равен zero. As в результате теплота трения может вызвать очень большое изменение соотношения теплообменников. Вязкая нефть.
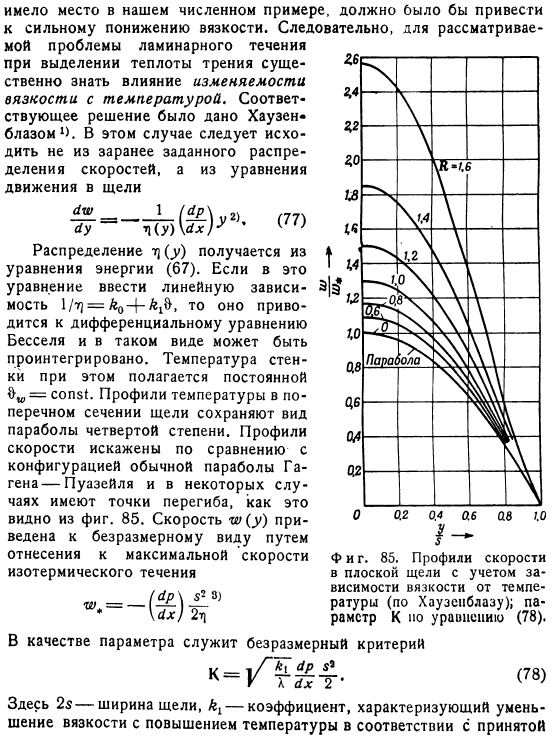
Но эти высоковязкие жидкости характеризуются очень выраженной температурной зависимостью вязкости. Поэтому температура повышается примерно на 30°C、 Где 2s-ширина щели, kt-коэффициент, характеризующий уменьшение вязкости при увеличении температуры в соответствии с допустимой температурой. Более высокие зависимости*).На стене касательные всех профилей скорости имеют одинаковый угол наклона. Это связано с тем, что здесь вязкость всегда t) w, зависящая от температуры стенки 8W. и При увеличении K расход также увеличивается, по сравнению с расходом изотермического потока, приблизительно в 1,5 раза в 2 раза.
Сравнение с приближенным решением, основанным на параболической интерполяции кривой вязкости, показывает, что более простое решение применимо, по крайней мере, до K = 1.7. Чтобы вычислить порядок ожидаемой величины, рассмотрим течение вязкого автола через щель шириной 2s = 20 мм (то есть s = 10″ 2 ig). Поскольку перепад давления составляет 1 атм на длину канала 0,1 м, dp! DX = =10kG1m. автоматическая теплопроводность X = 0.0148 кг! Sec * deg (см. стр. 248), и Вязкость t] = 20 ° C при 0.08119 кг-с / мг, Т)= 40°C при 0.020808 применение линейной интерполяции к этому интервалу^,= 1.787 мг1кг * ce » X x град.
Смотрите также:
| Предпосылки теории подобия | Гидродинамический и тепловой пограничные слои при ламинарном течении |
| Физический смысл критериев | Теплоотдача плоской пластины при постоянной температуре поверхности |

