Оглавление:
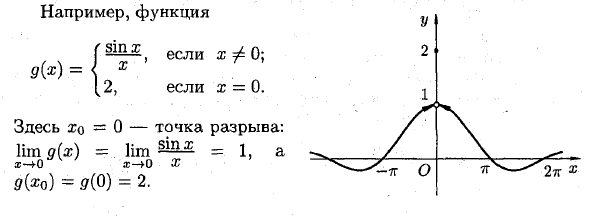


Точки разрыва функции и их классификация
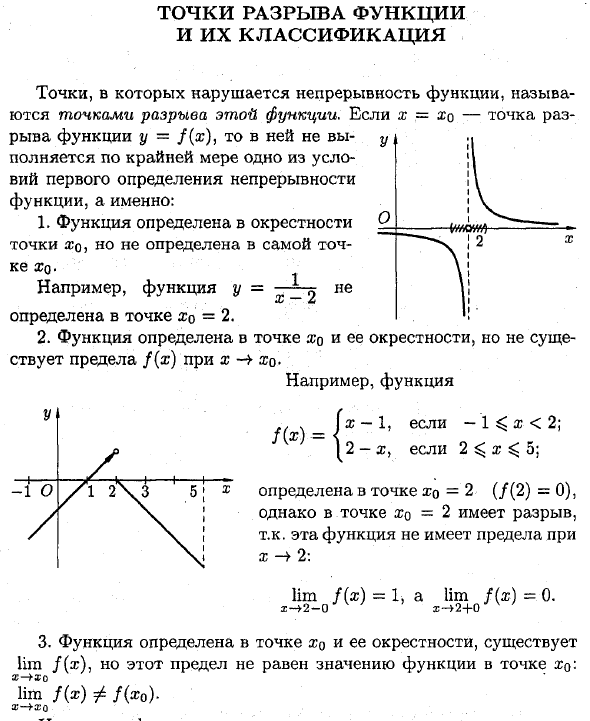
- Функциональные точки останова и их классификация Точки, которые нарушают непрерывность функции, называются точками останова для этой функции. Если x = x0 является разрывом функции y = f (x), то хотя бы одно из условий для первого определения непрерывности функции не выполняется. То есть: 1. Функция определена около точки x0, но не в самой точке Xq. Например, функция у = —Ц ^ X л Определено с точкой x0 = 2. 2.
Например, функция y> / h fx-1, если-1 ^ x <2; 7W = <0 0. , — ^ 2-х, если 2 ^ х ^ о; Он определен в точке x0 = 2 (/ (2) = 0), но в точке x0 = 2 имеется разрыв. Эта функция не имеет ограничений, таких как x-> 2. lim / (π) = 1, lim fix) = 0 x-> 2—0 4 7 x до> 2 + 0 V ‘ 3. Функция определена и существует в точке x0 и ее соседях lim / (x), но этот предел не равен значению функции в точке x0: x- * xo lim} {x) Φf (x0). X- * X0 Например, функция Где x0 = 0 — разрыв: lim d (x) =. 9 Ы = 9 (0) = 2. если x> 0; 2, если x = 0.2 часа
Функция определена в точке Xo и ее окрестности, но x xo не имеет предела f (x). Людмила Фирмаль
Все точки останова в функции делятся на точки останова типа 1 и типа 2. Разрыв x0 называется первым видом разрыва функции y = f (x). На этом этапе имеется конечный предел (односторонний предел) слева и справа от функции, т.е. lim fix) = Ai и lim fix) = A2. В этом случае: а) Если A \ = A2, точка x0 называется устранимым разрывом. б) Для AiÀA2 точка X0 называется конечным разрывом. Значение | A \ -Ai | Первый вид разрыва называется функцией скачка.
| Применение эквивалентных бесконечно малых функций | Основные теоремы о непрерывных функциях. Непрерывность элементарных функций |
| Непрерывность функций | Свойства функций, непрерывных на отрезке |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Если хотя бы один из односторонних пределов (левый или правый) не существует или равен бесконечности, разрыв x0 называется вторым видом разрыва функции y- / (x). Пример: 1. Используйте вышеуказанную функцию (см. Рисунок). y = x0 = 2 — это второй тип точки останова. 2. Для функции д *) = х ф о, х = о х-1, если-1 ^ х <2, 2-х, если 2 ^ х $ 5 xo = 2 — точка останова типа 1, а переход функции — (1-0) = 1. 3. Для функций F) = ho = 0 — первый тип съемной точки разрыва. Если x = 0, то gix) = 1 (вместо g (x) = 2) устраняет разрыв и делает функцию непрерывной. 4.
♦ Функция f (x) определена по оси значений и является непрерывной. 0 GL ti \ f 1 «pt x> n За исключением точки х = 3. Очевидно, что f [x) = < 1-1, если х <3 Фактически, lim fix) = 1 и lim fix) = -1. Таким образом, в точке х = 3 w-> 3 + 0 4 7 V 7 Существует первый вид пробела в функциях. Прыжок функции в этой точке равен 1 — (- 1) = 2.
По заданной функции f (x) = ^ — найти и найти разрывы О Х Их тип. Людмила Фирмаль

