Оглавление:
Все точки разрыва функции подразделяются на точки разрыва первого и второго рода.
Точка разрыва  называется точкой разрыва первого рода, если в этой точке существуют конечные левосторонние и правосторонние пределы, т.е.
называется точкой разрыва первого рода, если в этой точке существуют конечные левосторонние и правосторонние пределы, т.е. 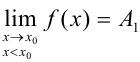 и
и 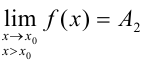 .
.
Если 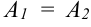 , то точка
, то точка  называется точкой устранимого разрыва, если
называется точкой устранимого разрыва, если 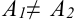 , то точка
, то точка  называется точкой конечного разрыва.
называется точкой конечного разрыва.
Точки разрыва первого рода можно представить следующим образом:

Точка разрыва  называется точкой разрыва второго рода, если в этой точке хотя бы один (левосторонний или правосторонний) предел равен бесконечности.
называется точкой разрыва второго рода, если в этой точке хотя бы один (левосторонний или правосторонний) предел равен бесконечности.
Точки разрыва второго рода можно представить следующим образом:
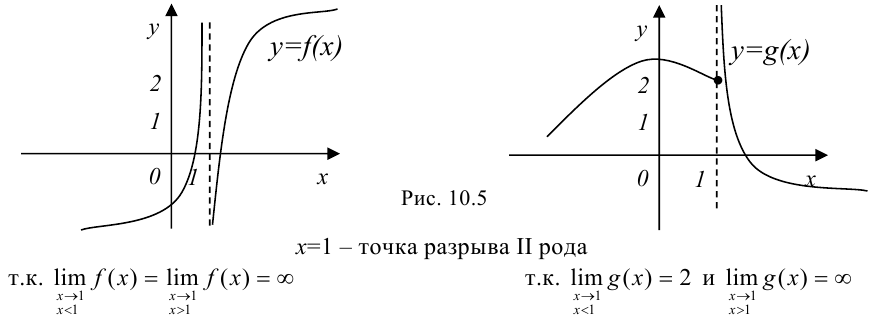
Можно привести много примеров хорошо известных нам основных элементарных функций, имеющих точки разрыва второго рода:
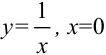 — точка разрыва II рода;
— точка разрыва II рода;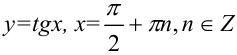 — точки разрыва II рода;
— точки разрыва II рода;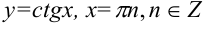 — точки разрыва II рода.
— точки разрыва II рода.
Рассмотрим на примере, как находить точки разрыва функции и определять их род.
Пример №10.3.
Найдите точки разрыва функции 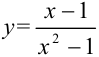 и определите их род.
и определите их род.
Решение:
Функция 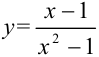 является элементарной, следовательно, она непрерывна на области определения.
является элементарной, следовательно, она непрерывна на области определения.
Найдем 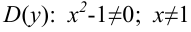 и
и 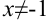 . Получили, что точки
. Получили, что точки 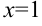 и
и 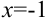 являются точками разрыва функции. Для того, чтобы их классифицировать, найдем предел функции в указанных точках.
являются точками разрыва функции. Для того, чтобы их классифицировать, найдем предел функции в указанных точках.
Для точки 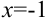
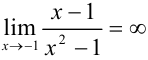 , следовательно,
, следовательно, 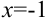 — точка разрыва II рода.
— точка разрыва II рода.
Для точки 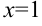
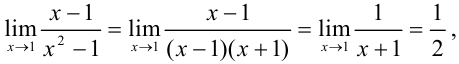
следовательно, 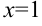 — точка разрыва I рода. Поскольку левосторонний и правосторонний пределы функции в этой точке совпадают, то
— точка разрыва I рода. Поскольку левосторонний и правосторонний пределы функции в этой точке совпадают, то 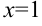 — точка устранимого разрыва. Положив
— точка устранимого разрыва. Положив 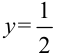 при
при 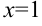 , разрыв устранится, функция станет непрерывной.
, разрыв устранится, функция станет непрерывной.
График данной функции представлен на рисунке 10.6.
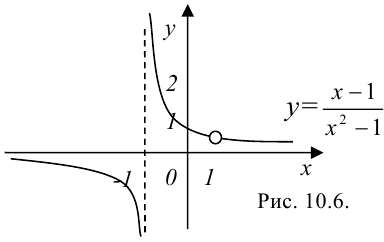
Пример №10.4.
Найдите точки разрыва функции 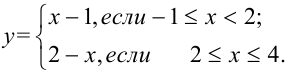 и определить их род.
и определить их род.
Решение:
Функция 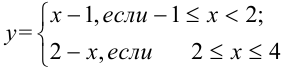 состоит из двух частей:
состоит из двух частей: 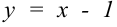 (при
(при 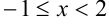 ) и
) и 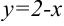 (при
(при 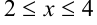 ). Функции
). Функции 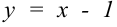 и
и 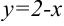 являются элементарными, непрерывными на множестве
являются элементарными, непрерывными на множестве  .
.
Имеет ли функция 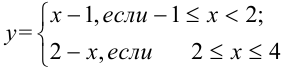 разрыв? Она определена во всех точках отрезка [-1; 4]. Найдем левосторонний и правосторонний пределы данной функции в точке
разрыв? Она определена во всех точках отрезка [-1; 4]. Найдем левосторонний и правосторонний пределы данной функции в точке 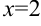 .
.
Левосторонний предел: 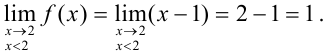
Правосторонний предел: 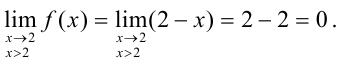
Поскольку левосторонний и правосторонний пределы функции конечны, то 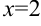 — точка разрыва I рода. Но эти пределы не равны между собой, следовательно,
— точка разрыва I рода. Но эти пределы не равны между собой, следовательно, 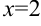 — точка конечного разрыва.
— точка конечного разрыва.
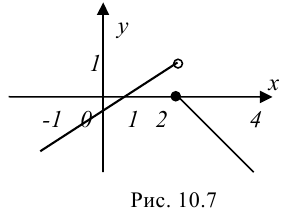
График данной функции представлен на рисунке 10.7.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Свойства функций, непрерывных на отрезке. |
| Непрерывность элементарных и сложных функций. |
| Понятие производной функции. |
| Нахождение производных основных элементарных функций. |

