Точки перегиба
Говорят, что в интервале 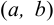 кривая вогнута, если все точки этой кривой лежат не ниже любой ее касательной в этом интервале.
кривая вогнута, если все точки этой кривой лежат не ниже любой ее касательной в этом интервале.
Говорят, что в интервале 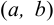 кривая выпукла, если все точки этой кривой лежат не выше любой ее касательной в этом интервале.
кривая выпукла, если все точки этой кривой лежат не выше любой ее касательной в этом интервале.
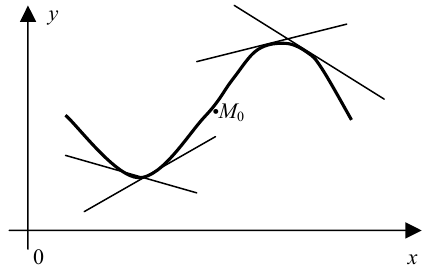
Теорема. Интервалы, в которых дуги кривой выпуклы, определяются из неравенства 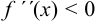 , а интервалы, в которых дуги этой кривой вогнуты, — из неравенства
, а интервалы, в которых дуги этой кривой вогнуты, — из неравенства 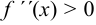 .
.
Точка кривой, отделяющая её выпуклую дугу от вогнутой, называется точкой перегиба.
Точки кривой, в которых 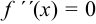 или
или 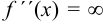 , а также те из них, в которых
, а также те из них, в которых 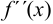 не существуют, называются критическими точками второго рода.
не существуют, называются критическими точками второго рода.
Точки перегиба следует искать среди критических точек второго рода.
В критической точке второго рода 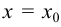 перегиб будет только в том случае, если при переходе через эту точку
перегиб будет только в том случае, если при переходе через эту точку 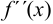 меняет знак.
меняет знак.
Правило. Для определения точек перегиба кривой надо определить все критические точки второго рода и рассмотреть знаки 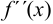 в каждых двух соседних интервалах, на которые эти точки делят область существования функции. В случае, если знаки
в каждых двух соседних интервалах, на которые эти точки делят область существования функции. В случае, если знаки 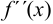 в двух соседних интервалах различны, критическая точка второго рода является точкой перегиба. Если же в двух соседних интервалах
в двух соседних интервалах различны, критическая точка второго рода является точкой перегиба. Если же в двух соседних интервалах 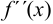 имеет один и тот же знак, то в рассматриваемой критической точке второго рода перегиба нет. В точке перегиба кривая пересекает касательную.
имеет один и тот же знак, то в рассматриваемой критической точке второго рода перегиба нет. В точке перегиба кривая пересекает касательную.
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:

