Точка описывает плоскую кривую так, что проекция ее скорости на ось сохраняет все время постоянную величину

Задача №4.

Точка описывает плоскую кривую так, что проекция ее скорости на ось 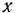сохраняет все время постоянную величину . Зная радиус кривизны траектории и скорость точки в каждый момент времени определить величину и направление ускорения этой точки.

Решение:

Согласно условию задачи, ускорение может быть направлено только по оси 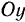(рис. 12). Вектор ускорения имеет две проекции на естественные оси, одна из которых равна 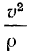, а вторая 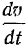. Проекция вектора скорости на ось 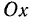равна 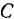. Из подобия треугольников имеем

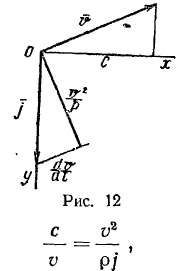
где 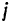— ускорение точки. Отсюда получим

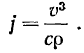
Аналитическое решение этой же задачи можно получить из определения радиуса кривизны траектории

Подставляя сюда значения 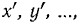будем иметь

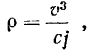
откуда непосредственно следует ответ задачи.

Задача взята со страницы подробного решения задач по всем темам теоретической механики:

Решение задач по теоретической механике

Возможно эти дополнительные задачи вам будут полезны:

Задача №2. Ползун приводится в движение вдоль стержня при помощи нити, продетой через неподвижное кольцо и наматывающейся на колесо, вращающееся с постоянной угловой скоростью (рис.-2). Определить скорость ползуна как функцию расстояния , если , а радиус колеса равен.

Задача №3. Ползун приводится о движение посредством нити, наматывающейся на шкив радиуса . Определить скорость ползуна в зависимости от расстояния , если угловая скорость шкива равна (рис. 3).

Задача №5. Точка описывает плоскую траекторию. Зная радиус кривизны этой траектории и скорость изменения угла, образуемого вектором скорости с некоторой неподвижной прямой, определить скорость точки.

Задача №6. Определить тангенциальную и нормальную составляющие ускорения материальной точки, движение которой задано уравнениями