Оглавление:
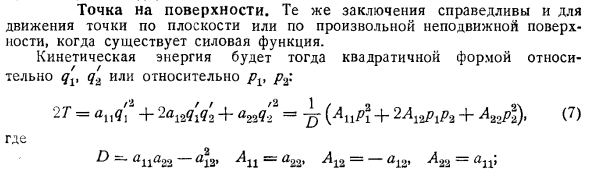


Точка на поверхности
- Тот же вывод справедлив и для движения точек вдоль плоскости или любой неподвижной поверхности при наличии силовой функции. Кинетическая энергия находится в форме 2 го порядка для qv q2 или pv p2. = 4 4 s 11 1 4 4 22 1. Куда YTsL23 13 11 = 22 12 = 12 23 = 11 8 H равна Т Якоби уравнение Э Вт. Если W a, a, h является полным интегралом, то уравнение траектории будет dW, s.
Материальная точка, находящаяся в плоскости под действием силы, имеющей определенную силовую функцию, выходит из начала О с заданной начальной скоростью. Людмила Фирмаль
Изучение этих свойств находится в книге lemon sur la ceolie Des surfaces d Album, Том 2. Главы VI и VII. Движение самого parabola. As для движения параболы тяжелых точек в вертикальной плоскости я нашел следующее пункт 302 с От точки x0, yo до точки jq, yi величина действия вдоль одной из двух параболических траекторий равна = Х х0 а 2л аз 2gyt 3 2л А3 2 У0 3 Где a 2 из 1 корней уравнения. 1 1 1 о + J и 2л 9 2 г 3 2L 3 2 yo 3 = О. 9 Это уравнение, после приведения к разумной форме, становится уравнением велосипедного движения относительно A.
- После выбора 1 из значений a2 знак величины a определяется по формуле 9. Здесь коэффициенты членов jq a0 и p имеют известный знак. Совершающему поступательное движение. Полученные из них следствия подтверждаются наблюдениями. Гюйгенс был продолжателем Галилея в теории движения точки. область механики открытием закона всемирного тяготения. Мы не ставим своей целью дать критический анализ основных законов механики.
Определить таутохрону для тяжелой точки в вертикальной плоскости, принимая во внимание трение и сопротивление среды, пропорциональное ц3. Людмила Фирмаль
Мы будем относить положение всех тел к некоторой системе осей, которые, по определению, мы будем считать абсолютно неподвижными осями. центре тяжести солнечной системы и с ребрами, направленными на три звезды, называемые неподвижными звездами. космографии. положение геометрической точки. Такую частицу материи называют материальной точкой.
Смотрите также:
Решение задач по теоретической механике

