Задача №7.
Точка движется по винтовой линии с постоянной по величине скоростью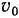 
. Определить величину и направление ускорения и радиус кривизны траектории точки.
Решение:
Параметрические уравнения винтовой линии имеют вид:
где 
— неизвестная функция времени, 
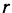и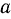 
— постоянные. Дифференцируя эти выражения, получим
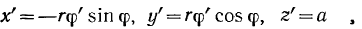
откуда
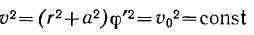
и
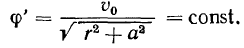
Проекции ускорения получают вид:
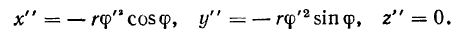
Из последних формул видно, что вектор ускорения расположен в плоскости, ортогональной к оси винта, а величина ускорения равна
Так как скорость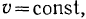 
то касательная составляющая ускорения обращается в нуль, то есть
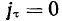
и, следовательно,
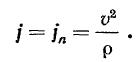
Подставляя значение 
в эту формулу, будем иметь
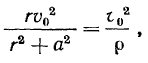
откуда
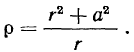
В этом случае вектор главной нормали к траектории точки направлен к оси винта, но радиус кривизны траектории оказывается больше радиуса винта. Полное ускорение тоже оказывается направленным по главной нормали. Такое расположение вектора ускорения обусловлено равномерностью движения точки по винтовой линии. Если же движение неравномерное, то появится еще и касательная составляющая ускорения.
При применении полярной системы координат необходимо помнить, что оси этой системы не являются неподвижными. Они вращаются. Это обстоятельство вносит ряд особенностей при вычислениях. Гак, если производная
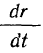
представляет собой проекцию скорости точки на радиус-вектор (радиальная составляющая скорости), то уже (проекция ускорения на радиус-вектор не будет равна второй производной от 
, то есть
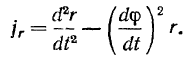
Задача взята со страницы подробного решения задач по всем темам теоретической механики:
Решение задач по теоретической механике
Возможно эти дополнительные задачи вам будут полезны:
