Типы шкал и методы измерения ощущений

Оглавление:

Любой вид измерения предполагает существование единиц измерения. Единица измерения — это, как сказал С. Стивенс, «мерило», которое является условным стандартом для выполнения определенных измерительных процедур. В науке и технике существуют стандартные единицы измерения, например, градусы, метры, амперы и т.д.

Психологические переменные, за некоторыми исключениями, не имеют собственных единиц измерения. Поэтому в большинстве случаев выраженность той или иной психологической характеристики определяется с помощью специальных измерительных шкал.

Шкала измерения — это базовое понятие, введенное в психологию С.С. Стивенсом в 1950 году; его интерпретация шкалы до сих пор используется в научной литературе.

Таким образом, присваивая номера объектам, создается шкала. Создание шкалы возможно потому, что существует изоморфизм формальных систем и систем действий на реальных объектах.

Числовая система — это множество элементов с реализуемыми на них отношениями, служащее моделью для множества измеряемых объектов.

Существует несколько типов таких систем и, соответственно, несколько типов весов. Операции, т.е. способ измерения объектов, определяют тип шкалы. Шкала, в свою очередь, характеризуется типом преобразований, которые могут быть присвоены результатам измерений. Если это правило не соблюдается, структура шкалы нарушается, и данные измерений не могут быть осмысленно интерпретированы.

Тип шкалы однозначно определяет набор статистических методов, которые могут быть применены для обработки данных измерений.

Шкала (лат. scala — лестница) — инструмент для измерения непрерывных свойств объекта; представляет собой числовую систему, в которой отношения между различными свойствами объекта выражаются свойствами ряда чисел.

P. Суппес и Дж. Зинес дали классическое определение шкалы: «Пусть A — эмпирическая система с отношениями (ESR), R — полная числовая система с отношениями (CSR), f — функция, гомоморфно отображающая A в подсистему R (если в области нет двух различных объектов с одинаковой мерой, что является изоморфизмом отображения). Назовем шкалу упорядоченной тройкой <A; R; f>».

Числовая система R обычно выбирается как система действительных чисел или ее подсистема. Множество A — это множество измеримых объектов с системой отношений, определенных на этом множестве. Отображение f — это правило, которое присваивает каждому объекту определенное число.

В настоящее время определение Suppes and Zines находится в стадии уточнения. Сначала в определение шкалы вводится G — множество допустимых преобразований. Во-вторых, множество A понимается не только как числовая система, но и как любая формальная знаковая система, которая может быть поставлена в отношение гомоморфизма с эмпирической системой. Таким образом, шкала — это четверка <A; R; f; G>. Согласно современным представлениям, группа G — это внутренняя характеристика шкалы, а f — лишь привязка шкалы к конкретной ситуации измерения.

В настоящее время измерение понимается как построение любой функции, которая изоморфно отображает эмпирическую структуру в символическую. Как упоминалось ранее, такая структура не обязательно должна быть числовой. Это может быть любая структура, которую можно использовать для измерения свойств объектов, заменяя их другими, более удобными (включая числа).

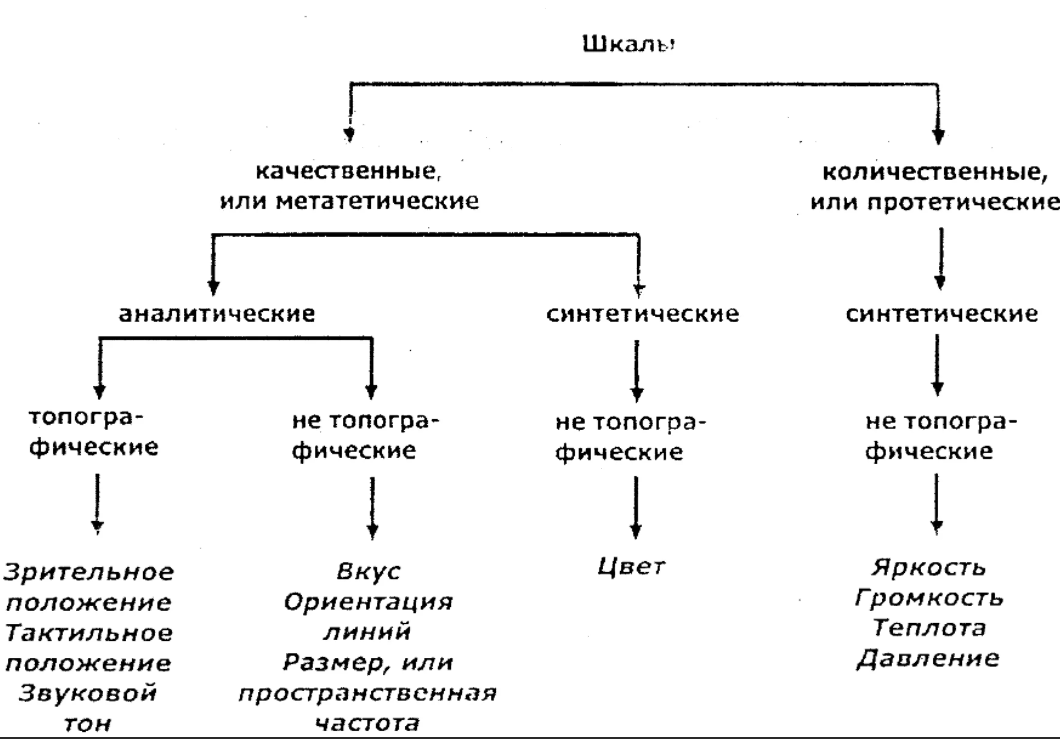
В психологии для изучения различных особенностей социально-психологических явлений используются различные шкалы. Первоначально выделяли четыре типа систем счисления, каждая из которых определяла четыре уровня или шкалы: 1) шкала наименований — номинальная; 2) шкала порядков — порядковая; шкала интервалов — интервальная; 4) шкала отношений — пропорциональная.

Первые две шкалы называются неметрическими, вторые две — метрическими. Соответственно, в психологии мы также говорим о двух подходах к психологическому измерению: метрическом (более строгом) и неметрическом (менее строгом).

Ряд экспертов также проводят различие между абсолютной шкалой и шкалой различий.

Давайте рассмотрим особенности каждого типа весов.

Шкала пунктов

Шкала наименований возникает в результате присвоения «имен» объектам. Необходимо разделить множество объектов на непересекающиеся подмножества.

То есть объекты сравнивают друг с другом и определяют их эквивалентность-неэквивалентность. В результате процедуры формируется набор классов эквивалентности. Объекты, принадлежащие к одному классу, эквивалентны друг другу и отличаются от объектов, принадлежащих к другим классам. Эквивалентным объектам присваиваются одинаковые имена.

Операция сравнения является основной для построения любой шкалы. Для построения такой шкалы необходимо, чтобы объект был равен или подобен самому себе (x=x для всех значений x), т.е. на множестве объектов должно быть реализовано отношение рефлексивности. Для психологических объектов, таких как субъекты или психические образы, такое отношение возможно, если абстрагироваться от времени. Но поскольку операции попарного (в частности) сравнения множества всех объектов не реализуются одновременно эмпирически, это элементарное условие также не выполняется в ходе эмпирического измерения.

Следует помнить, что любая шкала — это идеализация, модель реальности, даже такая простая, как шкала имен.

На объектах должны быть реализованы отношения симметрии (R (X=Y) -> R (Y=X)) и транзитивности R (X=Y, Y=Z) -> R (X=Z)). Но по ряду результатов психологических экспериментов эти условия могут быть нарушены.

Более того, многократное повторение эксперимента (накопление статистики) приводит к «перетасовке» состава классов: в лучшем случае мы можем получить оценку, указывающую на вероятность принадлежности объекта к тому или иному классу.

Поэтому нет оснований говорить о шкале наименований (номинативной шкале или шкале строгой классификации) как о простейшей шкале, начальном уровне измерения в психологии.

Существуют и более «примитивные» (эмпирические, но не математические) виды шкал: шкалы, основанные на отношениях толерантности; шкалы «нечеткой» классификации и т.д.

Можно говорить о шкале наименований, когда эмпирические объекты просто «маркируются» числом.

Поэтому, если объекты эквивалентны в каком-то отношении, мы имеем право отнести их к одному классу. Главное, как сказал Стивенс, не присваивать один и тот же символ разным классам или разные символы одному и тому же классу.

Несмотря на тенденцию «переоценивать» значимость шкалы, психологи очень часто используют шкалу именования в исследованиях. «Объективные» процедуры измерения в диагностике личности ведут к типологизации: отнесению определенной личности к определенному типу. Примером такой типологии являются классические темпераменты: холерик, сангвиник, меланхолик и флегматик.

Простейшая номинативная шкала называется дихотомической. При измерении по дихотомической шкале измеряемые характеристики могут быть закодированы двумя символами или числами, например, 0 и 1, или 2 и 6, или буквами A и B, или любыми двумя символами, которые отличаются друг от друга. Характеристика, измеряемая по дихотомической шкале, называется альтернативной характеристикой. В дихотомической шкале все изучаемые объекты, характеристики или черты делятся на два непересекающихся класса, и исследователь спрашивает, «проявилась» ли интересующая его черта у испытуемого или нет.

Исследователь, использующий шкалу наименований, может применять следующие инвариантные статистики: относительные частоты, моды, корреляции случайных событий, критерий.

Сфера действия приказа

Если можно определить порядок психологических объектов по выраженности признака, используется порядковая шкала.

Порядковая шкала образуется, когда на множестве реализуется бинарное отношение — порядок (отношения «больше» и «меньше»). Построение порядковой шкалы — более сложный процесс, чем создание шкалы наименований. Он позволяет определить ранг или место каждого значения переменной по отношению к другим значениям. Этот ранг может быть результатом собственного ранжирования испытуемым определенных стимулов или их свойств (первичный показатель методик ранжирования или рейтинговых процедур), но он также может быть установлен экспериментатором как вторичный показатель (например, при ранжировании частот положительных ответов испытуемых на вопросы по различным темам).

Классы эквивалентности, выделенные с помощью шкалы наименований, могут быть упорядочены по определенному основанию. Различают шкалу строгого упорядочивания (строгое упорядочивание) и шкалу слабого упорядочивания (слабое упорядочивание). В первом случае на элементах множества реализуются отношения «больше чем» и «меньше чем», а во втором случае на элементах множества реализуются отношения «не больше или равно» и «меньше или равно».

Значения величин могут быть заменены квадратами, логарифмами, нормализациями и так далее. При таких преобразованиях значений величин, определяемых шкалой порядка, расположение объектов на шкале не меняется, т.е. инверсии не происходит.

Стивенс уже утверждал, что результаты большинства психологических измерений в лучшем случае согласуются с порядковыми шкалами.

Шкалы порядка широко используются в когнитивной психологии, экспериментальной психосемантике, социальной психологии: Ранжирование, рейтинг, даже образовательный, дают порядковые шкалы. Классическим примером использования порядковых шкал является тестирование личностных качеств, а также навыков. Однако большинство специалистов в области тестирования интеллекта считают, что процедура измерения этого признака допускает использование интервальных шкал и даже шкалы отношения.

В любом случае, этот масштаб позволяет нам представить линейное расположение объектов на оси свойств. Таким образом, вводится наиболее важный термин — измеряемое свойство, или линейное свойство, а в шкале наименований используется «вырожденная» версия трактовки термина «свойство»: «точечное» свойство (свойство есть — свойства нет).

Порядковая шкала (ранжирование) должна иметь не менее трех классов (групп): например, ответы на вопросы анкеты: «да», «не знаю», «нет»; или — низкий, средний, высокий; и т.д., чтобы измеряемые атрибуты можно было ранжировать. По этой причине шкала называется порядковой или ранговой.

Легко перейти от классов к числам, если считать, что низшему классу присваивается ранг (код или номер) 1, среднему классу — ранг 2, высшему классу — ранг 3 (или наоборот). Чем больше количество классов разделов всей экспериментальной совокупности, тем больше возможностей статистической обработки полученных данных и проверки статистических гипотез.

При кодировании порядковых переменных им могут быть присвоены любые цифры (коды), но эти коды (цифры) должны обязательно соблюдать порядок, то есть каждая последующая цифра должна быть больше (или меньше) предыдущей.

Для интерпретации данных порядковой шкалы можно использовать более широкий спектр статистических мер (в дополнение к тем, которые допустимы для шкалы наименований).

Медиану можно использовать в качестве центральной тенденции, а перцентили — в качестве диаграммы рассеяния. Порядковая корреляция (t-Канделла и p-Спирмена) позволяет установить взаимосвязь между двумя измерениями.

Числовые значения на порядковой шкале нельзя складывать, вычитать, делить или умножать.

Интервальная шкала

Шкала интервалов — это первая метрическая шкала. Собственно, исходя из этого, имеет смысл говорить об измерениях в узком смысле этого слова — о введении меры на множестве объектов. Шкала интервалов определяет размер разницы между объектами в проявлении того или иного свойства. Интервальная шкала может быть использована для сравнения двух объектов. В этом случае он используется для определения того, насколько больше или меньше конкретное свойство проявляется в одном объекте, чем в другом.

Интервальная шкала очень часто используется исследователями. Классическим примером использования этой шкалы в физике является измерение температуры по Цельсию. Интервальная шкала имеет единицу измерения, но положение нулевой точки на ней произвольно, поэтому нет смысла говорить, во сколько раз выше или ниже утренняя температура воздуха, измеренная по шкале Цельсия, чем дневная температура воздуха.

Интервальная шкала позволяет применять практически все параметрические статистики для анализа полученных с ее помощью данных. Помимо медианы и моды, среднее арифметическое используется для характеристики центральной тенденции, а дисперсия — для оценки дисперсии. Можно рассчитать коэффициенты перекоса и эксцесса и другие параметры распределения. Коэффициент линейной корреляции Пирсона и т.д. используется для оценки величины статистической связи между переменными.

Большинство экспертов в области теории психологических измерений считают, что тесты измеряют психические характеристики с помощью интервальной шкалы. Это касается, прежде всего, тестов интеллекта и достижений. Числовые значения одного теста можно преобразовать в числовые значения другого теста с помощью линейного преобразования: x’ = ax + b.

Ряд авторов считает, что нет никаких оснований соотносить тесты интеллекта с интервальными шкалами. Во-первых, в каждом тесте есть «ноль» — любой человек может получить минимальный балл, если не решит ни одного задания за отведенное время. Во-вторых, тест имеет максимальную шкалу — балл, который может получить сдающий тест, если он решит все задания за минимальное время. В-третьих, разница между оценками по каждой шкале неравномерна. По крайней мере, нет никаких теоретических или эмпирических оснований для утверждения, что 100 и 120 баллов по шкале IQ отличаются на столько же, на сколько 80 и 100 баллов.

Скорее всего, шкала любого теста интеллекта является составной шкалой, с естественным минимумом и\or максимумом, но порядковой. Однако эти соображения не мешают участникам тестирования рассматривать шкалу IQ как интервал и преобразовывать «сырые» баллы в баллы по шкале, используя привычную процедуру «нормализации» шкалы.

Установка масштаба

Шкалу отношений также называют шкалой равных отношений. Особенностью этой шкалы является наличие фиксированной нулевой точки, то есть полное отсутствие какого-либо свойства или признака. Шкала отношений является наиболее выразительной шкалой, которая допускает любые математические операции и использование разнообразных статистических методов.

Шкала отношений в принципе очень близка к интервальной шкале, потому что если начало координат строго фиксировано, то любая интервальная шкала становится шкалой отношений.

Шкала соотношений отображает данные о выраженности свойств объектов, когда можно увидеть, во сколько раз один объект больше или меньше другого.

Это возможно, только если, помимо определения равенства, рангового порядка и равенства интервалов, известно также равенство отношений. Шкала отношений отличается от шкалы интервалов тем, что на ней определено положение «натурального» нуля. Классическим примером является температурная шкала Кельвина.

В масштабах отношений проводятся точные и сверхточные измерения в таких науках, как физика, химия, микробиология и так далее. В реляционной шкале проводятся точные и сверхточные измерения в таких науках, как физика, химия, микробиология и т.д.

Измерение массы, времени реакции и усвоения тестовых заданий — это применение шкалы соотношений.

Разница между этой шкалой и абсолютной шкалой заключается в том, что здесь нет «естественной» единицы шкалы.

Дихотомическая классификация часто рассматривается как вариант шкалы наименований. Это верно за исключением одного случая, когда мы измеряем свойство, которое имеет только два уровня выражения: «является — не является», так называемое «точечное» свойство. Примеров таких свойств много: наличие или отсутствие наследственного заболевания (дальтонизм, синдром Дауна, гемофилия и т.д.), абсолютный слух и т.д. В этом случае исследователь имеет право «оцифровать» данные, присвоив каждому из типов номер «1» или «О», и работать с ними, как со значениями интервальной шкалы.

В отличие от шкалы соотношений, шкала разностей не имеет естественной нулевой точки, но имеет естественную единицу измерения. Она соответствует аддитивной группе вещественных чисел. Классическим примером такой шкалы является историческая хронология. Она аналогична интервальной шкале. Единственное отличие заключается в том, что значения этой шкалы нельзя умножить (разделить) на константу. Поэтому считается, что шкала различий — единственная, обладающая точностью стратификации. В психологии шкала различий используется в методах попарного сравнения.

Абсолютная шкала является дальнейшим развитием шкалы соотношений и отличается от нее тем, что имеет естественную единицу измерения. В этом заключается его сходство со шкалой различий. Количество решенных задач («сырой» балл), когда задачи равны, является одним из проявлений абсолютной шкалы.

Абсолютные шкалы не используются в психологии. Данные, полученные с помощью абсолютной шкалы, не преобразуются, шкала идентична самой себе. Любая статистическая мера приемлема.

В литературе, посвященной проблемам психологического измерения, упоминаются и другие типы шкал: порядковая шкала (ординальная) с естественным происхождением, логарифмический интервал, упорядоченная метрика и так далее.

Все написанное выше относится к одномерным шкалам. Шкалы также могут быть многомерными: Масштабная характеристика в этом случае имеет ненулевые проекции на два (или более) соответствующих параметра. Векторные признаки, в отличие от скалярных, являются многомерными.

На странице курсовые работы по психологии вы найдете много готовых тем для курсовых по предмету «Психология».

Здесь темы рефератов по психологии

Читайте дополнительные лекции: