Оглавление:








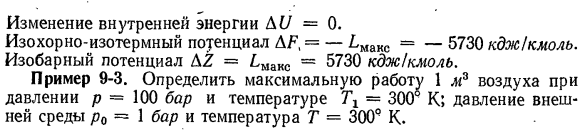


Тепловая теорема Нернста
- Теорема nernstheat Экспериментальное исследование свойств различных веществ при сверхнизких температурах привело к открытию важной новой закономерности, названной тепловой теоремой Нернста. Теорему Нернста часто называют третьим законом термодинамики, поскольку она не подчиняется первому и второму законам термодинамики, а выражает новые законы природы. В настоящее время этот закон можно вывести из основных
положений квантовой статистики. Теорема Нернста была впервые установлена при определении химического сродства, но позже было обнаружено, что она имеет более Правильное решение проблемы химического сродства было дано Вант-Хоффом. Он показал, что химическое сродство не является термическим эффектом, и если
широкие последствия, чем только решение этой проблемы. Людмила Фирмаль
реакция организма протекает при постоянной температуре и давлении, то она должна измеряться уменьшением изобарного потенциала AZ, или если организм реагирует при постоянной температуре и объеме уменьшением изобарного потенциала AF. это хорошая идея.& F = L>и работа L, которая является мерой сродства, определяется уравнением Гиббса-Гельмгольца. Л = Г +Γ(-0.Коэффициент теплового расширения тела и тепловой коэффициент давления yt равны следующим значениям: 1 фдв \ 1 /
ДП \ Но из уравнения (9-2) (МДТ) Р = И из Формулы (9-20) (др / ДТ) 0 И так оно и есть.、 1 / ДС \ — огонь (dslddp) = (ДС / ДВ) ту 1 (ДС Из теоремы Нернста следует, что энтропия не изменяется при T 0, то есть она не зависит от p и v, поэтому—> 0 а 0, то YT-> — о Или коэффициент теплового расширения и коэффициент теплового давления исчезают в T 0. Отношение CP и cv емкости Γ0.Поскольку производная равна нулюсправочная формула (6-45) v и(ds! dT) p равно T — > 0, и тепловые емкости cv и co вблизи абсолютного нуля температуры также
- исчезают. То есть в T, c 0 0 и cp — > 0. 0. Абсолютный ноль недоступности температуры. Рассматривая процесс циркуляции, Нернст пришел к выводу, что такого течения в конечных измерениях не существует- «процесс циркуляции, в котором тело охлаждается до абсолютного нуля». 。 Рассмотрим цикл Карно температуры sink=т радиатора и температуры Т2 = о радиатора (рис. 9-8). Согласно второму закону термодинамики, для циклический процесс,$ йй / Т =О или AS12 + As23 4 — As34 + As41 =О, где As12 = г / Г; As23 = 0 (процесс изоляции);
с положениями раздела 34 = 0,As41 = 0 (процесс изоляции). который допускает непрерывную работу с охлаждением 1 теплообменника, можно создать вечный двигатель 2-го рода, что, согласно 2-му закону термодинамики, невозможно. Поэтому абсолютного нуля температуры достичь невозможно. Однако получение температуры, сколь угодно близкой к 7 = 0, не исключено. В 7 ФТ * ф г 1 \( 4 TgO 3 _
Таким образом, в результате проведения такого цикла, Людмила Фирмаль
5 Рисунок 9-8 вопросы и примеры тестирования в главе IX 1.Что представляет собой термодинамическая идентичность? 2.Каковы функции термодинамических функций? 3.Какие термодинамические функции считаются элементарными? 4.Какая независимая переменная определяет каждую основную термодинамическую функцию? 5.Что такое изотермический потенциал и связанная с ним энергия? 6.Изометрический физический смысл изотермического
потенциала. 7.Какова общая энергетическая ценность системы? 8.Уравнение Макса Гиббса-операция Гельмгольца на постоянном ТВ и тр. 9.Что такое величина, называемая термодинамическим потенциалом? 10.Каковы химические потенциалы? 11.To к какому классу относятся термодинамические системы? 12.Фазовое преобразование типа 1 и типа 2 ′ 13.Какие условия называются стабильными, нестабильными и метастабильными? 14.Какие условия необходимо реализовать для устойчивого равновесия
термодинамических систем? 15.Условия равновесия однородной системы. ’16.Условия равновесия нескольких стадий материи. 17.Фаза/) Г-ди грамм. .18.Фазовая диаграмма pV. 19. ^- Диаграмма. 20.Уравнение Клапейрона Клаузиуса и его производные. 21.Тепловая теорема Нернста. Пример 9-1.Докажите, что это идеальный газ (ДФ / ДТ) Р = — С-Р и (dFldp) м = — В. «» Для независимых переменных p и T изобарный изотермический потенциал Z является характеристической функцией. Z-и-TS + pV = F +
pV или F = Z-pV. При постоянном давлении, дифференцируя последнее уравнение относительно t、 (ДФ / ДТ) Р =(дз / ДТ) р-р(дв / ДТ) р. > Из уравнения Клапейрона (дв / ДТ) р = р / P и (ДВ / ДП) Т = — РТ / Р2.Учитывая уравнение (9-25) и Клапейрона, получим (dF / dT) p = — S-p (R / p)= — S-R. При постоянной температуре, если мы дифференцируем потенциал Z против p、 (ДФ / $ п) м =(дз / ДП) М-р(дв / ДП) М-V Если рассматривать уравнение (9-25) и Клапейрона、 (dFldp) м = В-В-В = — \ Л Пример 9-2. Определить L, Q, D/, AU, AS, AF и AZ при температуре 1000°к= изотермическое расширение 1 кмоль идеального газа от 1,0
до Р2〜0,5 бар. Использование расширения Isobar Л = 1000-8314. 2. 2. 3 log 1 / 0.5 = 5730 кДж! Моль. % ♦ Тепловложение Q = L = 5730 кДж / кмоль в процессе. Изменение энтальпии D / = 0.Изменение энтропии А = М / Т = 5730/1000-5.73 kdoy!(Кмоль-град) B изменение внутренней энергии AU = 0 Изотермические изотермы по отношению к AF], AF generic,= — LMaKC =-5730 кДж / кмоль. Изобарный потенциал AZ = ^ max = ^ 730 кДж / кмоль. Пример 9-3.Определить максимальную
работу воздуха при давлении p = 100 бар, температуре Tx = 300 К, 1 м3.Давление окружающей среды p0 = 1 бар и температура T = 300 r K ’макс = («1 -» 2)-т0(СЛ-Sjj)+ ПО(на VX-П2) Или / max = c0 (7 \ — Γ0) — Γ0 (cp в TJT, — R в Pl! Po)+ Rp0 (’TJPl — ВПО.)、 ’Макс-300-0.287″ 2.3 журнал 100-ф-0.287(300/100-300)= = 311 кДж / кг. авиационный корпус: m =(piVJ / iRTj)=(100•105)/(287•300)= 116 кг; — LMaK0 = 31M16 = 36100 кДж. Пример 9-4.Докажите следующее соотношение: У = з-Т(дз! ДТ) в-п (дз / ДП) М \ ЧВ-Т(d2F! DT1) v \ Cp—T(d2Z / dT%\ ’(dU / dV) s = (dF / dV) m; (dUAp) s =(dZ / dp) m;>(dFldT) v =(dZ / dT)p (dF / dV)m =
положений квантовой статистики. Теорема Нернста была впервые установлена при определении химического сродства, но позже было обнаружено, что она имеет более широкие последствия, чем только решение этой проблемы. Правильное решение проблемы химического сродства было дано Вант-Хоффом. Он показал, что
химическое сродство не является термическим эффектом, и если реакция организма протекает при постоянной температуре и давлении, то она должна измеряться уменьшением изобарного потенциала AZ, или если организм реагирует при постоянной температуре и объеме уменьшением изобарного потенциала AF. это хорошая идея.& F = L>и работа L, которая является мерой сродства, определяется уравнением Гиббса-Гельмгольца. Л =
Г +Γ(-0.Коэффициент теплового расширения тела и тепловой коэффициент давления yt равны следующим значениям: 1 фдв \ 1 / ДП \ Но из уравнения (9-2) (МДТ) Р = И из Формулы (9-20) (др / ДТ) 0 И так оно и есть.、 1 / ДС \ — огонь (dslddp) = (ДС / ДВ) ту 1 (ДС Из теоремы Нернста следует, что энтропия не изменяется при T 0, то есть она не зависит от p и v, поэтому—> 0 а 0, то YT-> — о Или коэффициент теплового расширения и коэффициент теплового давления исчезают в T 0. Отношение CP и cv емкости Γ0.Поскольку производная равна
v и(ds! dT) p равно T — > 0, и тепловые емкости cv и co вблизи абсолютного нуля температуры также исчезают. То есть в T, c 0 0 и cp — > 0. 0. Абсолютный ноль недоступности температуры. Рассматривая процесс циркуляции, Нернст пришел к выводу, что такого течения в конечных измерениях не существует- «процесс циркуляции, в котором тело охлаждается до абсолютного нуля». 。 Рассмотрим цикл Карно температуры sink=т радиатора и температуры Т2 = о радиатора (рис. 9-8). Согласно второму закону
термодинамики, для циклический процесс,$ йй / Т =О или AS12 + As23 4 — As34 + As41 =О, где As12 = г / Г; As23 = 0 (процесс изоляции); с положениями раздела 34 = 0,As41 = 0 (процесс изоляции). Таким образом, в результате проведения такого цикла, который допускает непрерывную работу с охлаждением 1 теплообменника, можно создать вечный двигатель 2-го рода, что, согласно 2-му закону термодинамики, невозможно. Поэтому абсолютного нуля температуры достичь невозможно. Однако получение температуры, сколь угодно близкой к 7 = 0, не исключено. В 7 ФТ * ф г 1 \( 4 TgO 3 _
5 Рисунок 9-8 вопросы и примеры тестирования в главе IX 1.Что представляет собой термодинамическая идентичность? 2.Каковы функции термодинамических функций? 3.Какие термодинамические функции считаются элементарными? 4.Какая независимая переменная определяет каждую основную термодинамическую функцию? 5.Что такое изотермический потенциал и связанная с ним энергия? 6.Изометрический физический смысл изотермического потенциала. 7.Какова общая энергетическая ценность системы? 8.Уравнение Макса Гиббса-операция Гельмгольца на постоянном ТВ и тр. 9.Что такое величина, называемая термодинамическим потенциалом? 10.Каковы химические потенциалы? 11.To к какому классу относятся термодинамические системы? 12.Фазовое
преобразование типа 1 и типа 2 ′ 13.Какие условия называются стабильными, нестабильными и метастабильными? 14.Какие условия необходимо реализовать для устойчивого равновесия термодинамических систем? 15.Условия равновесия однородной системы. ’16.Условия равновесия нескольких стадий материи. 17.Фаза/) Г-ди грамм. .18.Фазовая диаграмма pV. 19. ^- Диаграмма. 20.Уравнение Клапейрона Клаузиуса и его производные. 21.Тепловая теорема Нернста. Пример 9-1.Докажите, что это идеальный газ (ДФ / ДТ) Р = — С-Р и (dFldp) м = — В. «» Для независимых переменных p и T изобарный изотермический
потенциал Z является характеристической функцией. Z-и-TS + pV = F + pV или F = Z-pV. При постоянном давлении, дифференцируя последнее уравнение относительно t、 (ДФ / ДТ) Р =(дз / ДТ) р-р(дв / ДТ) р. > Из уравнения Клапейрона (дв / ДТ) р = р / P и (ДВ / ДП) Т = — РТ / Р2.Учитывая уравнение (9-25) и Клапейрона, получим (dF / dT) p = — S-p (R / p)= — S-R. При постоянной температуре, если мы дифференцируем потенциал Z против p、 (ДФ / $ п) м =(дз / ДП) М-р(дв / ДП) М-V Если
рассматривать уравнение (9-25) и Клапейрона、 (dFldp) м = В-В-В = — \ Л Пример 9-2. Определить L, Q, D/, AU, AS, AF и AZ при температуре 1000°к= изотермическое расширение 1 кмоль идеального газа от 1,0 до Р2〜0,5 бар. Использование расширения Isobar Л = 1000-8314. 2. 2. 3 log 1 / 0.5 = 5730 кДж! Моль. % ♦ Тепловложение Q = L = 5730 кДж / кмоль в процессе. Изменение энтальпии D / = 0.Изменение энтропии А = М / Т = 5730/1000-5.73 kdoy!(Кмоль-град) B изменение внутренней энергии AU = 0 Изотермические изотермы по отношению к AF], AF generic,= — LMaKC =-5730 кДж / кмоль. Изобарный потенциал AZ = ^
max = ^ 730 кДж / кмоль. Пример 9-3.Определить максимальную работу воздуха при давлении p = 100 бар, температуре Tx = 300 К, 1 м3.Давление окружающей среды p0 = 1 бар и температура T = 300 r K ’макс = («1 -» 2)-т0(СЛ-Sjj)+ ПО(на VX-П2) Или / max = c0 (7 \ — Γ0) — Γ0 (cp в TJT, — R в Pl! Po)+ Rp0 (’TJPl — ВПО.)、 ’Макс-300-0.287″ 2.3 журнал 100-ф-0.287(300/100-300)= = 311 кДж / кг. авиационный корпус: m =(piVJ / iRTj)=(100•105)/(287•300)= 116 кг; — LMaK0 = 31M16 = 36100 кДж. Пример 9-4.Докажите следующее соотношение: У = з-Т(дз! ДТ) в-п (дз / ДП) М \ ЧВ-Т(d2F! DT1) v \ Cp—T(d2Z / dT%\ ’(dU / dV) s = (dF / dV) m; (dUAp) s =(dZ / dp) m;>(dFldT) v =(dZ / dT)p (dF / dV)m =
Смотрите также:
Решение задач по термодинамике
| Термодинамические диаграммы | Приложение дифференциальных уравнений к решению некоторых термодинамических задач |
| Уравнение Клапейрона — Клаузиуса | Основные понятия и определения водяного пара |

