Оглавление:














Теплопроводность при нестационарном режиме
- Если теплопередача в теле зависит как от координаты, так и от времени (теплопроводность в нестационарных условиях), то это объясняется. Теплопроводность в процессе работы Долгое время инженеров интересовал нестационарный режим нагрева металла для различных технических операций, например, ковки, штамповки, закалки и др. Нестационарный режим.
С появлением сверхзвуковых самолетов, ракетных двигателей и др., интерес к процессу теплопроводности в нестационарных условиях представляет growing. In некоторые случаи Рекомендуется рассчитать теплозащиту головки ракеты или стенок камеры сгорания и сопла двигателя с учетом нестационарного режима работы. Дело в том, что самолет и его Двигатель может работать в очень короткие сроки, поэтому тепловой процесс элементов конструкции не успевает выйти на стационарный режим.
Переходные процессы характеризуются переходом от одного стационарного режима к другому. Людмила Фирмаль
Нестационарный режим Теплопроводность является периодической или переходной. Периодический режим называется режимом, в котором определенное распределение температуры повторяется через определенное время Промежуток времени, любое количество раз. В практике технических, временных Процесс более распространенный, поэтому он будет рассмотрен подробно. § 1.
Общее решение уравнения 1-мерной теплопроводности уравнение нестационарной теплопроводности( Теплота тела) имеет вид dT dT, T = f (x, y, zₜt),= — коэффициент теплопроводности, ПК. Для 1-D уравнение упрощается следующим образом: Вычислите уравнение (V-1) методом разделения переменных таким же образом, как это было сделано при решении уравнения(V-1).Решение(V-1) находится в следующем виде: T = f (x, t)= X (x)F (t), где (V-2), X — он работает только с x. F является функцией только m.
Подставляя формулу (V-1) в (V-2) и деля ее на произведение X (x) F (x), i gx i 1 dF / watch X ’dx * A F dx * ’» один раз слева Равенство (V-3) является функцией только x, а правая сторона является функцией только r. Это означает, что он не изменяется в x и m. то есть, 1 d * X 1 X dxz «и J_dF F dx = const. Где уравнение (V-3) разбивается на 2 обыкновенных дифференциальных уравнения (V-4) и имеет формулу (V-4) для d ^ X dx2 = — ±k2X (V-5) (4-L2 Следующее общее решение: X =С₁ ??* — pC₂e-Ч (V-6) и (- k2) для X-Coscos KX 4-csinsin KX. (U-7).
Обыкновенное дифференциальное уравнение (V-5)решается путем разделения переменных — = ±е * ал. После интегрирования этого уравнения в F — ±k2at4-InC₅ получается и записывается общее решение (±&2) (V-8) (v-5).Используется для общих решений (V-6), (V-7) и (V-8 Получить конкретное решение конкретной проблемы теплопередачи. Уравнение (V-6) предполагает экспоненциальное распределение температуры, а уравнение (V-7) допускает разложение Распределение бесконечных строк.
Уравнение (V-8) является периодическим, если экспоненциальное распределение температуры (знак минус экспоненциальный) или k2 является мнимым. Размер. Форма общего решения формулы (V-1) (для-k2) такова: Tg-XF =(Coscos KX +c₄sin KX) c₅e-AK * X. заметим, что решение уравнения не всегда является функцией (Теплопроводность) может быть выражена как произведение 2 функций, каждая из которых зависит только от 1 переменной. Например, решением уравнения (V-1) является следующая функция: (k -) 1Т=С, −1 —е (V-10) для подтверждения этого различают (V-10) относительно m, x (V-H) и подставляют результат в (V-1).
Последние 2 уравнения идентичны друг другу other. In другими словами, (V-10) является Решение (V-1). § 2.Неограниченная теплопроводность плоской стенки рассмотрим процесс охлаждения плоской стенки 2 /толщина (рисунок V-1).Температура стенки T равна、 направление оси X. Такое ограничение возможно в любом из 2 Условий.1. размеры стенки в направлении осей Y и Z не ограничены, то есть теплоотвод с конца.
Стена не искажает температурное поле в направлении оси X. 2. второе условие обеспечивает полную изоляцию торцов, но размеры стен в направлении оси y и оси z、 С конечным размером. если r = 0, то стенки начальной температуры T0, одинаковые во всех точках поперечного сечения, вступают в контакт с жидкостью при температуре Tf В. Процесс охлаждения стен не происходит change. It удобно использовать Tf в качестве точки отсчета температуры. То есть более сложные случаи, в которых to-f (x) рассматривается в специализированной литературе (57].
Инжир. V I. нестационарная теплопроводность плоской стенки t0 1 l 1 отсчитывает другие температуры от T{0.Коэффициент теплопередачи от стенки к жидкости а Он считается знаменитым. Математическая постановка задачи включает в себя тепловые уравнения, начальные условия и граничные условия. Тепловое уравнение рассматриваемого случая (V-1).
Форма, записанная с избыточной температурой Φ= T-Tf, является dx2a dt(V-12), а граничные условия (начальные и граничные) могут быть записаны в виде: начальное условие 1) m-0 0 = TQ-Tf = Oo для — / x c /; если граничное условие 2) (x> 0, — I = 0,\ dx, 1x = 0, потому что плоскость симметрии пластины проходит x = 0, 3) m> 0 =.в случае 5L прямая цитата.
Рассматриваемый В этом случае температура во всех точках стенки уменьшается со временем, поэтому нужно выбрать константу в следующем виде:— здесь Л2> 0.Имея это в виду, общее решение (V-9) является Напишите в виде О=СБе » Аач»c₃coskx4-c₄sin KX). Для определения константы (V-13) (V-13) используйте начальные условия 1, 2, 3.Во-первых, мы используем граничное условие 2. = МКО-ac2x (- C₃ksinkx + СК coskx).Это выражение должно быть равно нулю при x = 0./ ?Потому что # = 0, так как x = 0 и k cos k x, постоянная константа равна нулю, то есть С0.
Должно быть равно = 0. Форма (V-13) равна d = 0″ ALC cos kx. (V-14) чтобы найти собственные значения k =kₙ, используйте граничное условие 3.производная (V-14) относительно X —=〜Ce-ak2xk sin kx. dх(в-15) Найдите (V-14) Се ^ ⁴ = —V COS KX и замените его на (V-15). в результате DX — — -/?Вы получаете Sin£x. последняя форма уравнения cos kx x = / is-MtgW. \ dx> x ^ 1 I. наконец, применить Граничное условие 3, Get-kft / ₓₑ / TGA?/ = откуда последнее выражение может быть переписано в виде cigP-al X P -£/. Комплекс значений (в-16) био-критерии (II1-11) знаменатель(в-16).
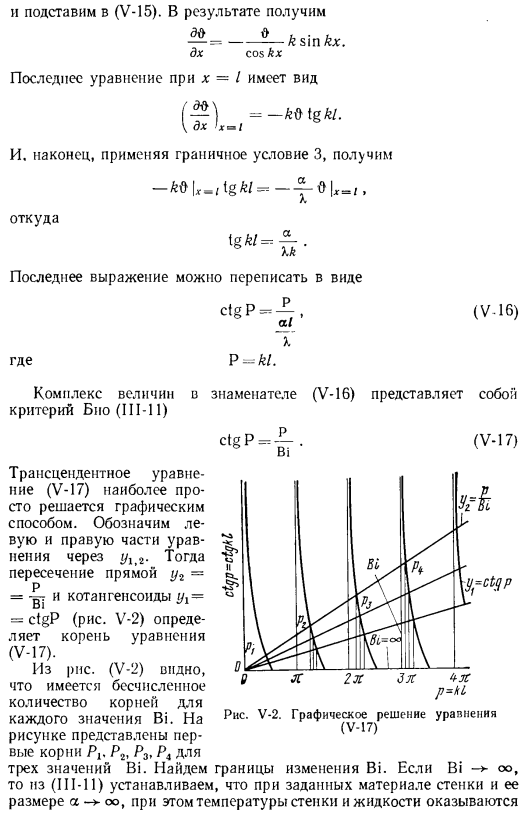
Трансцендентальное уравнение (V-17) легче всего решить графически. Левая и правая части уравнения являются Z/₁>.Далее, пересечение линии y₂-P = — gj и котангентоид yx = = ctgP (рисунок V-2) определяет корень уравнения (V-17).Из рисунка(Фау-2)видно, что каждому значению BI имеет бесчисленное множество корней. На фото Первый корень Р₂, Р₃ р₃ и Р₄ отображаются для 3 значений BI. (Sh-11) температура стенки и жидкости относительно конкретного материала стенки и ее размер A°C Получилась фигура V-2.
Графическое решение граничного уравнения bi (V-17). Для Bi oo p равно. Прямая y., = y. совпадает с абсциссой и корни уравнения (V-14) равны:= ПЗ = уу……….. A =(2 «-1) y (V-18) (n = 1, 2, 3, Если Bi — > 0, то a — > 0 и (ft) ₓ ₌ Z-oo-to-TF, для P теплопередачи от пластины к жидкости Pet: прямая y₂ = — G-is Корни оси ординат и уравнения (V-17) равны:/ =(n-1) l. (n = 1, 2,…(V-19) для каждого значения Bi в диапазоне 0 Biкраевая задача (V-12)、(1)-(3)дополнительные сведения см. В разделе практическое руководство: 0 = 2 C. форма cosfo-Me»■, (V-20) i = 1. 2 X1 ■ константа.
C определяется начальным условием 1.формула для r-0, 0-Oo для — / x /(V-20) принимает вид Oo = 2ciC⁰s (pi7 -)- Легко показать, что система функций 1 = 1,2 \1 (V-21) (Pn-положительный корень трансцендентного уравнения) ортогональна на отрезке| 0,Z], то есть если/#= / 0 #= 0 i = j. легко указать / o. So, чтобы найти его, действуйте следующим образом (закон Фурье): умножьте обе стороны (V-21) на cos y x и интегрируйте x в интервале 10, Z].И затем… Получить силу ортогональности системы/ / ДХ, (в-22) dxo2sⁱⁿp1⁰Pi-sin Пи, потому что Пи (в-23) в окончательном виде с DX материи.
Дж потому что Х) DX = ДХ, потому что — если значение Cₜ из с i-vo / (V-23) подставляется в Формулу (V-20), то можно записать решение о охлаждении plate. So, 00 — = y » О_ _ _ _ 2 sin Pj Pi — Ф-грех, потому что Пи п — ф = 1,2 а-2sⁱⁿP * ⁴pi — / — грех, потому что Пи-Пи или (V-17), потому что? Ввиду…?11 (V-24) (V-25) (V-26) A = f_lV4 ′ 2BⁱAnd2+ P? * ’^(Би ^ Би + Р? Анализ ) ’ Решение (V-2 4). Выражение с учетом (V-26) (V-24) может быть выражено в виде обобщенной переменной в виде следующей зависимости (111-15): а r / n-ar x\, — CV |> p’i)•, где числовой Фурье.
В случае охлаждения стенки, учитывая обозначение (V-27), зависимость (II1-15) находим в температурном поле стенки, что очень хлопотно (V-28) по формуле (V-24) — e F (Bⁱⁱt) Это требует времени. Поэтому в инженерной практике мы решаем такие задачи с помощью номограмм, которые строятся в виде уравнений (V-28).Обычно создается номограмма. Получены следующие значения безразмерных координат: -= 0 / x 1 и m = 1, что соответствует центру стенки (плоскости симметрии) и ее внешней поверхности.
Согласно каждому из (V-28) В такой номограмме B принимается за температуру интересующей безразмерной переменной, а число Фурье био-за безразмерную независимую переменную. Если дело имеет конкретное решение Когда тело охлаждается в виде (V-28), оно сохраняет свою прочность в случае нагрева, при определении 015]и параметра-Крит-Т / — К(V-29) Температура тела 7 ′ ₀ — начальная температура тела; T-температура среды для мытья тела.
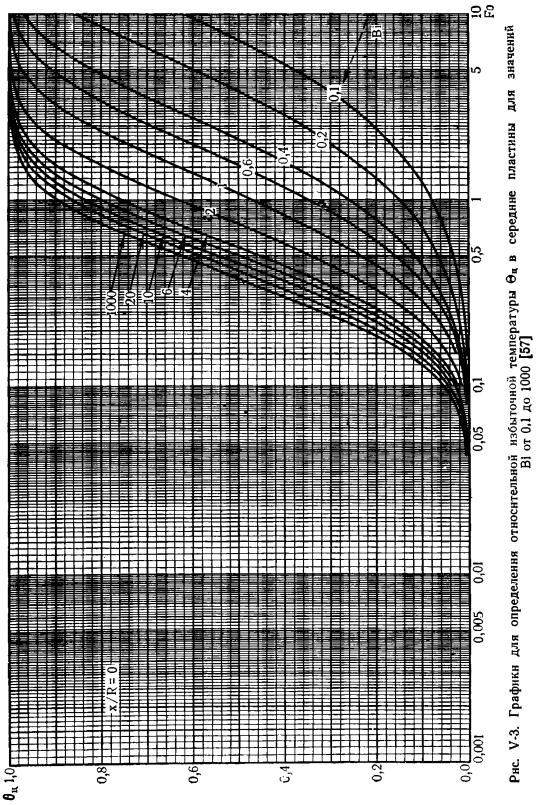
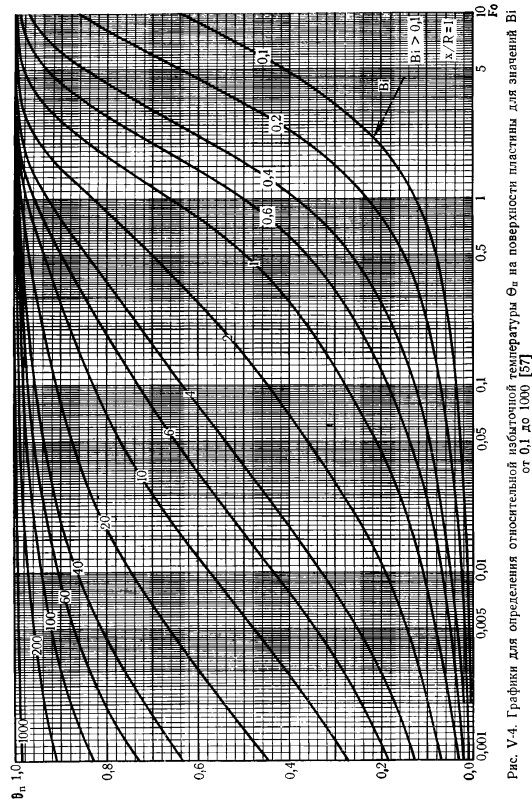
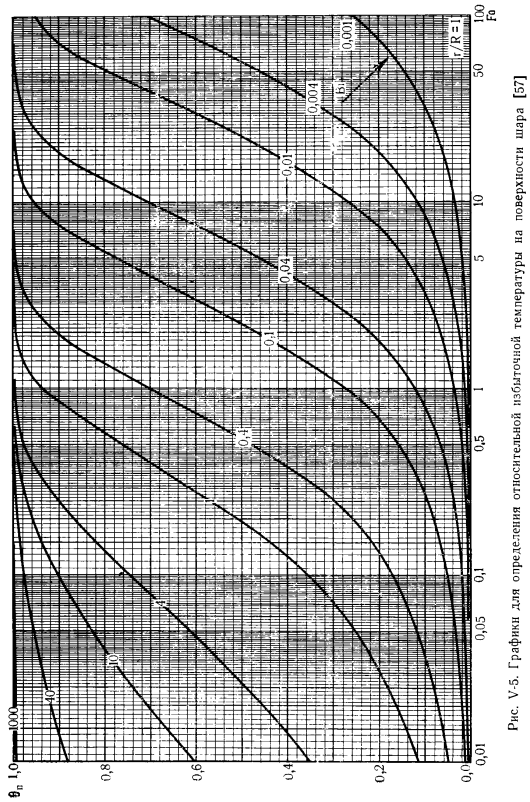
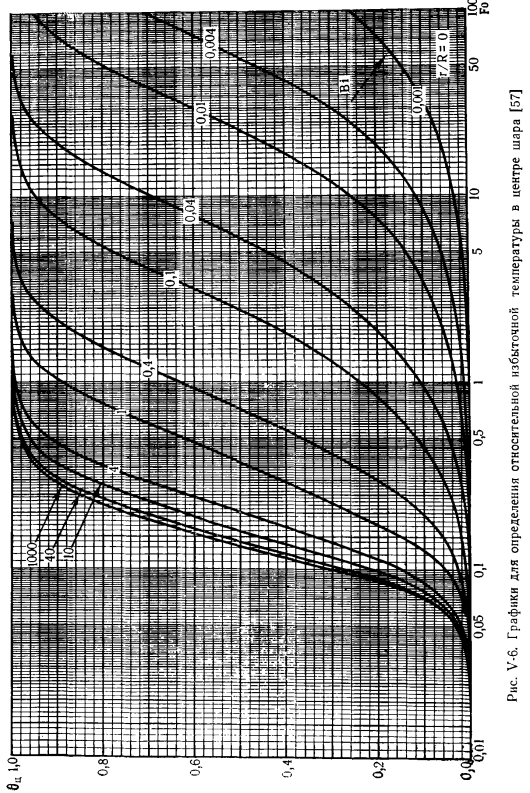
Рисунки V-3 и V-4 являются номограммами для определения безразмерной температуры [57]6 (V-27) центр (симметричная плоскость) и стороны пластины. Не менее интересны и другие тела простой формы, например, аналогичные решения шариков и цилиндров (V-24). Бесконечная длина. Аналитические решения с громоздкостью не показаны here. In обобщенные переменные, форма решения как шара, так и цилиндра аналогична (V-28). На рисунках V-5 и V-6 показана номограмма для определения безразмерной температуры B(U-27) поверхности шара (безразмерные координаты-5 =1.г-текущий радиус, R-радиус шара) ivcentresreshold ^безразмерные координаты при нагреве.
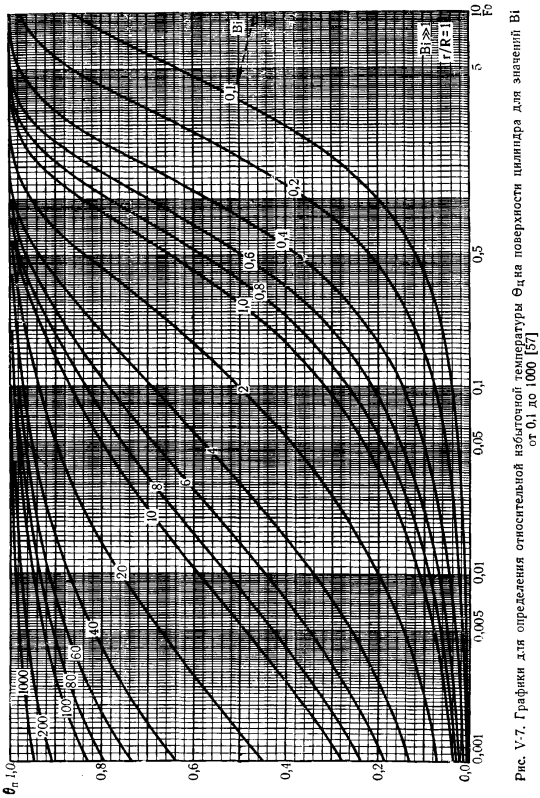
В стандарте Biot радиус шара вводится как характерный размер. Цифры V-7 и V-8 являются номограммами для определения. Безразмерная температура на поверхности бесконечного цилиндра B (V-27) (безразмерные координаты= 1) и координаты-0) вводит радиус цилиндра R. (Рис. V-3, V-4, V-5, V-6, V-7 и V-8): число Фурье Fo = — и ссылка Bi =(оси Fo и Bi определяют все значения для определения цилиндра^безразмерный. Био-критерии в качестве характерного размера РНС. В-3. Для значения Bi 0,1-1000 составлен график для определения относительного превышения температуры 0С в середине пластины [57] V-4.
Для значения Bi 0,1-1000 составлен график для определения относительной избыточной температуры поверхности пластины 6a[57] V-5.График для определения относительного избытка Температура поверхности шара [57]рисунок V-6.График для определения относительной избыточной температуры центра шара[57] рис. V-7.График для определения относительного избытка Темпера! 0.1-1000 [57] 5 0.5 10 вам нужно знать 0 цилиндрической поверхности с Bi-значением).
Далее от точки на горизонтальной оси номограммы, где абсцисса равна i’o、 Восстановите перпендикуляр к точке пересечения с линией, соответствующей полученному значению Bi-в ординатах точки пересечения будет искомая безразмерная температура 9.Продолжать. Анализ решений (V-24).Дело Би — > ОО. Для данного материала X и размера стенки I условие Bi — > oo эквивалентно a — > — oo. Это значит что термальное сопротивление к передаче тепла Стенка 1 / а против жидкости равна нулю.
Это означает, что на протяжении всего процесса охлаждения наружная поверхность стенок и температура жидкости остаются равными друг другу. В этих условиях (V-18) Л =(2л-1), а коэффициент Aₜ(в-25) — это 2 греха Пи Р4-грех, потому что Пи пт 2 Син | [(2Н ->) Ф | (2л — — 1)г + грех(2 ″ — — 1) г Кос =( -!) «+>(V-30) cos(2n-1) — = 0 2 решение Подставляя значения Ai из (V-30) в (V-24), мы получаем рассматриваемый случай. То есть, (2l — 1) l X exp 4 —— cos /(2l −1) l для определения 2 (2d −1) 2L* ar 4 p (V-3I) скорость изменения.
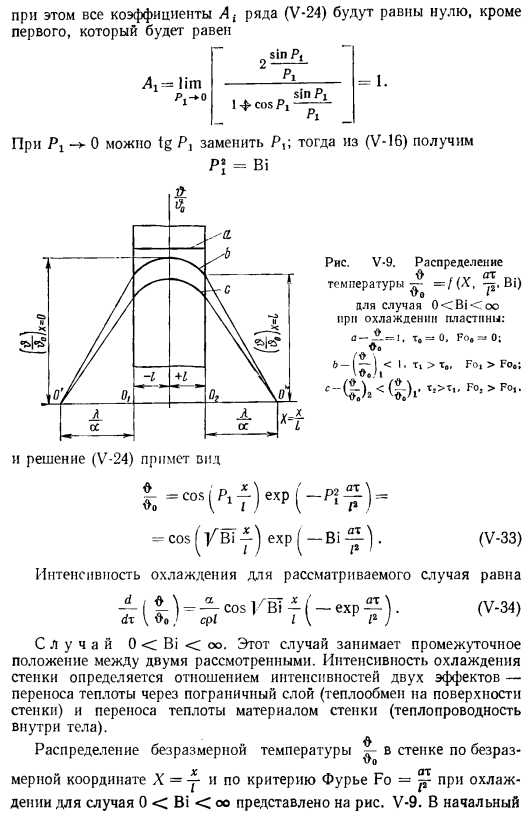
Из основное направление температура стенки х (прочность охлаждение)(в-32) (в-32), эта стена охлаждая сила (б = /(% ) свойства)、 Коэффициент теплопроводности a. если значение критерия БИО очень мало (Bi 0,1). Bi — > ■для 0, (V-19) (n-1) l, согласно 4(2l-1) l’, Все коэффициенты A {серия (V-24) Он равен нулю, с первым исключением равным 1.Для 1-COS Pi Pl Pi-Pj — > 0 можно заменить tg Pi на P. тогда из (V-16) получается, когда пластина охлаждается.
- И решение (V-24) принимает вид: В-9.Случай 0 Bioo распределение температуры y = /(X сила охлаждения рассматриваемого случая .(Bi) (V-33) равна d dr (V-34) случай 0 Bi. в этом случае Между 2 промежуточными позициями рассмотрены. Скорость охлаждения стенки определяется отношением интенсивности 2 эффектов-теплообмена через пограничный слой (Передача тепла в стене) и передача тепла материалом стены(термальной проводимостью в теле).
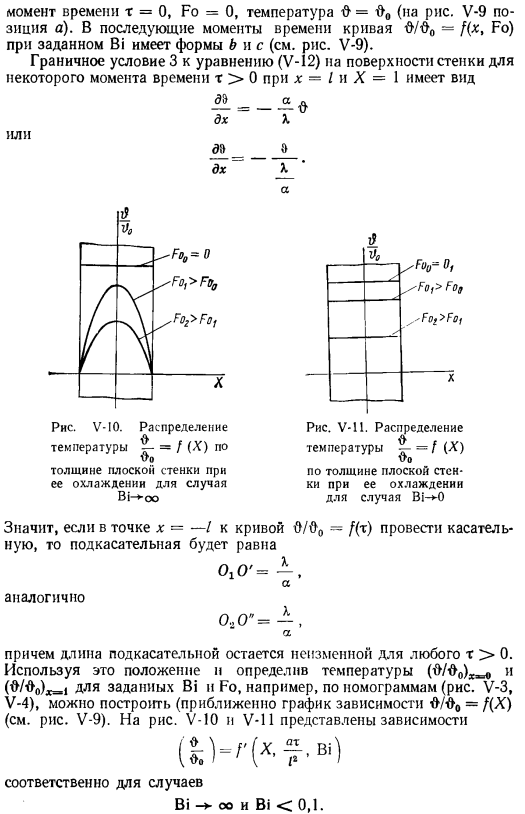
Безразмерное распределение температуры стенок по безразмерной координате X =y, а биопоказано при охлаждении Фурье-ориентированного Fo = случай 0. V-9.At первый момент, m = O, Fo = O, температура Φ= Oo(положение V-9, положение a). Итак… В более поздний момент времени форма кривой-f (x, Fo) Bi равна b и c (см. Рисунок V-9).В течение некоторого времени выполняется граничное условие для уравнения стенки (V-12) 3 время x> 0 для x = I и X = 1 имеет следующий вид или oY _ _ _ _ _ 0_ dx X Av-I0.
Касательная равна O, а O ’ = a равно O. Людмила Фирмаль
Распределение температуры£ — = / ( * ) PO VO рисунок V-11.VO над распределением температуры$ — = / (X) толщина Плоская стенка — толщина плоской стенки при охлаждении для корпуса Bi — >oo ki — >0 при охлаждении для case. So если мы проведем касательную линию в точке x = ~ / кривая О/Оо-F (X)、 длина касательной не изменяется при r> 0.Это положение используется для определения температуры (I>/^₀) X₀₀ И (M> 0) x = 1 для заданных Bi и Fo, например, из номограммы (рис. V-3, V-4) можно построить(почти граф зависимостей Ф/Фо= /(X) (см. рис.) V-9).
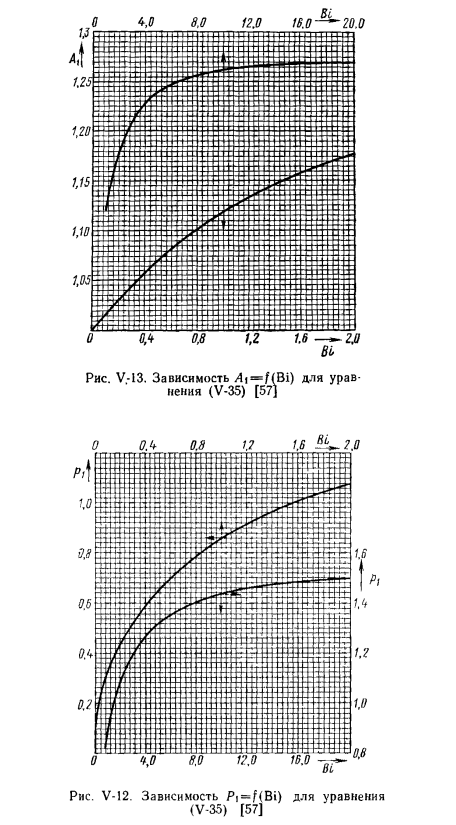
Показаны рисунки V-10 и V-11 Зависимости.£( ) = «(*Рис. V. для −13, соответственно, у-в0, зависимости зависимостей / выражений (V-35) / h = f (Bi) [57]рис. V-12.F (Bi) [57]продолжение зависимости Pj =выражение (V-35) Анализ решений (V-24). Значение Pₜ представляет собой ряд возрастающих чисел Р1Рг * * * число ряда членов PF (V-24) быстро уменьшается с увеличением членов. Как вы увеличиваете значение Pᵢₜ в этом случае? То есть серия(V-24) сходится быстро. Из (V-24), для большого числа Фурье Fo, ряд сходится быстрее, чем для малого числа Фурье.
Для машиностроения Если уравнение (V-24) уже вычислено при Fo 0.3, то оно может быть ограничено только первым членом ряда*, и при этом принимает вид „l d x-P * — =A_cosposposp-e“, что значительно simplified. To решай Для величины Ax и Px можно использовать графики= /(Bi) (рисунок V-12) и Aₜ= / (Bi) (рисунок V-13) 157).Определение расхода тепла. Расход тепла на кубический метр материала охлаждаемая за время от m-0 до m = Tj стенка определяется по формуле: Q =Ф[Оо-0 (г)], (V-35) рис. V-14.
Определение средней температуры O (t)по толщине стенки Уравнение(V-36) (V-36), где О (г)-средняя температура M = Tj толщины стенки в конкретный момент (рисунок V -!4).Температура 0(t)、 Функция от 0 до Z(V-24), то есть найти область под кривой 0 (x, Tj)и разделить результат на I (рисунок V-14): Ieo _ _ Qpₙ2axflfl (Ti)» i L11 ″ Cos Pi-DX-BZ=i1oCos- дуплексный. Начиная с 1l, первое число в серии sin-pT — *(V-24) равно x / 1 = 0, Bi = = 1, Fo> 0.55 [57J .
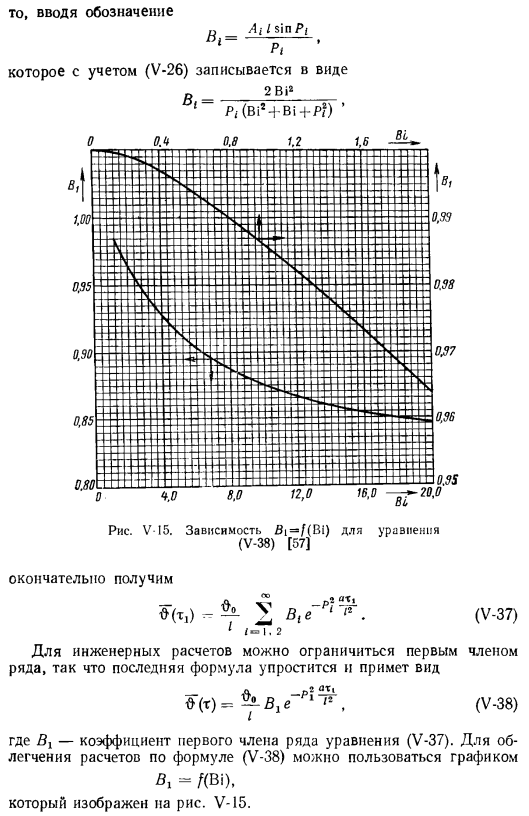
Далее введем обозначение/ 1 / / sin Рассматривая P / P /(V-26), он обозначается как 2Bi2. В-И5.Зависимость формулы (V-38) Bi = /(Bi) [57]что в итоге получается-АС -/>? ^ — 1-v 2 ve•(V-37) » / ask = 1.2 для В инженерных расчетах последняя формула упрощается, и lДТ1А (т) = = ^ — вхе(V-38) может быть ограничена первым членом ряда, так что здесь коэффициент первого члена ряда уравнений (V-37).для облегчения расчета по формуле(V-38) можно использовать график-/(Bi). В-15. § 3.
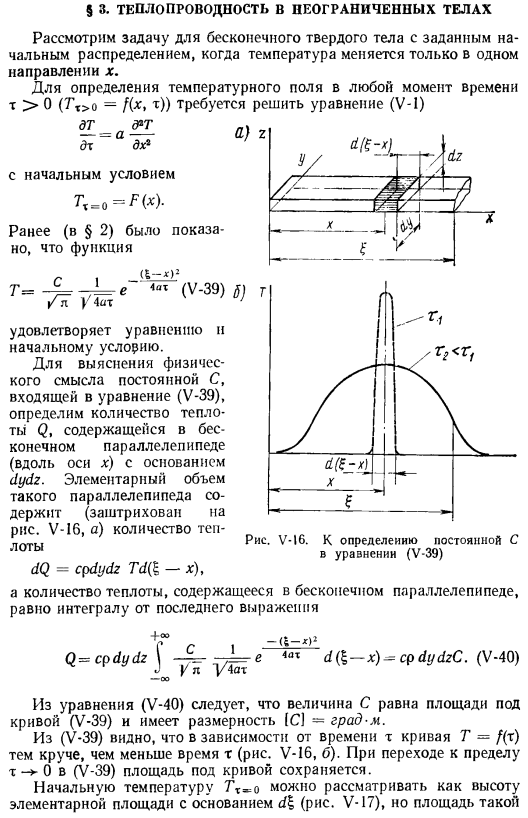
Теплопроводность с неограниченным телом Бесконечное твердое тело с заданным начальным распределением, где температура изменяется только в одном направлении x. To определить температурное поле в любой момент времени t> 0 (Tm> o = Dx, m)) начальное условие Tₓ ₌ Q = f (x) должно решить уравнение (V-1) dt _ d * t DX〜a DX^.Ранее (§ 2) Функция (V-39) | l / 4at удовлетворяла уравнению、 Начальная state.
To уточним физический смысл константы с, содержащейся в формуле (V-39), определим количество теплоты Q, содержащейся в бесконечном ящике (вдоль оси x на базе dydz. Основной объем такого параллелепипеда содержит количество теплоты dQ = cpdydz Td (±- х) (заштриховано рисунком V-16,а). V-I6.To определите константу C из Количество тепла, включенное в уравнение (V-39) и поле Бесконечности, будет равно Интегралу последней Формулы cpdydz j j-OOC__ 1_ u l [Аат-CI-XP tax D (I-x) ^ cpdydzc.
Из Формулы (V-40) (V-40), величина C равна площади под кривой (V-39), размерность[C]-град-м. Из (V-39), в зависимости от времени t, кривая T = f(t) Чем круче, тем короче время t(рисунок V-16, б). Переход в (V-39) к пределу m — > 0 сохранит область ниже кривой. Начальная температура, Tx = 0, может рассматриваться как высота элементарного Площадь основания d% (рисунок V-17), но площадь таких участков постоянна C. используя (V-40) и учитывая, что базовый участок должен использовать dQ вместо Q, рисунок V И7.
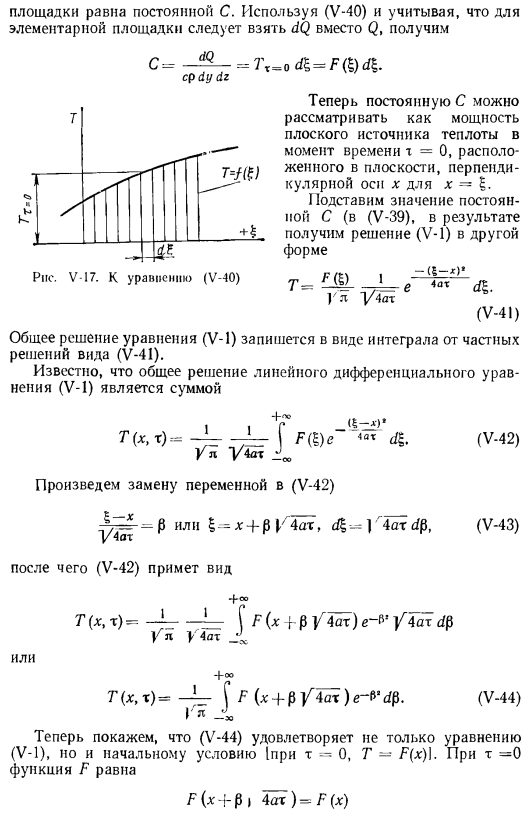
Для уравнения (V-40), t = odB = F ( £ ) d£.Где константу С можно рассматривать как выход плоского источника тепла с временем 1 = 0 в вертикальной плоскости. X =ось x£.Если подставить значение константы C ((V-39)), то в результате получим решение (V-1) в другом виде), общее решение формулы (V-1)описывается .
Интегралом от частного Форма решения (V-41). известно, что общее решение линейного дифференциального уравнения (V-1) является суммой (V-42).(V-42) -] 4pt dp.] / 4ag = p или заменить переменную x + p 1/4 оси, то (V-43) (V-42)+°T (x, m)= ——-(F (X b P 4ax) e〜^ 4 при dB / I V4at X или T (x, x)= f F (x h-f f4ax) dp.(V-44) тогда, (V-44) Выполняется не только формула (V-1), но и начальные условия(если m = 0, то T-F(x)].если m = 0, то функция F равна F(x + p> 4ax)= F (x) и( V-44)равна Ch-oo 7(x, m = 0) = — ЛФ(х)е — » ДП. V L-so 4-00 5 e-t’dfi = Yi, oo T(x, x = 0)-F(x)следовательно, функция(V-44) удовлетворяет начальному условию. § 4.
Теплопроводность в полуограниченном теле 1D температурное поле (1-мерная материя) рассматривает теплопроводность объекта, который простирается бесконечно в направлении оси±g /;и-f-x является и отделяется плоскостью. перпендикулярно оси x при x = 0; такое тело называется semi-bounded. To определив температурное поле, необходимо решить уравнение (V-1) с начальным условием T(x,0)= F(x). = T0 = const и граничные условия T (0, t) — = 0.В качестве точки отсчета используется температура Tw.
Вам нужно найти зависимость y — = F (x, r). Используйте 1о для определения желаемой зависимости Решение (V-42), полученное для неограниченного body. To для этого продолжите функцию Γ (x) в отрицательном направлении и установите начальную температуру F (- x) на-F (x).С этим. Продолжение F (x = 0)= 0, условие поверхности выполнено, и решение x> 0 совпадает с решением исходной задачи (рисунок V-18).Обозначим Интеграл (V-42).
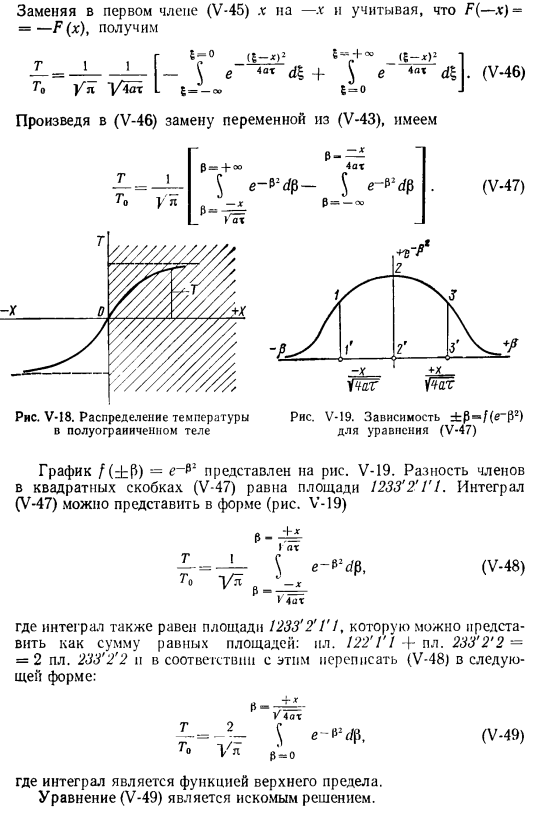
Как сумму 2 из двух терминов 1/ + +°°(£-) + Замените x в первом члене 5⁴atd£(V-45) (V-45) на x и получите F (- x)= — F (x) (V-46) из (V-43).、 (V-47) рис V-18.Распределение температуры в полу-ограничение тела V-19.Для уравнения зависимости±p/(e «p2) (V-47) график f (iP)=показан на рисунке V-19. Квадратные скобки (V-47) равны площади 123&2 ′ G1.Интеграл (V-47) может быть выражен в следующем виде(рисунок V-19): T I Go 1 / l $ e-!!- Да. — X U 4ax(V-48), Интеграл также равен площади 1233 ′ 2 ′ Г1 Его можно представить как сумму равных площадей: Ил. 122 ′ Г1 ч-ЛП.
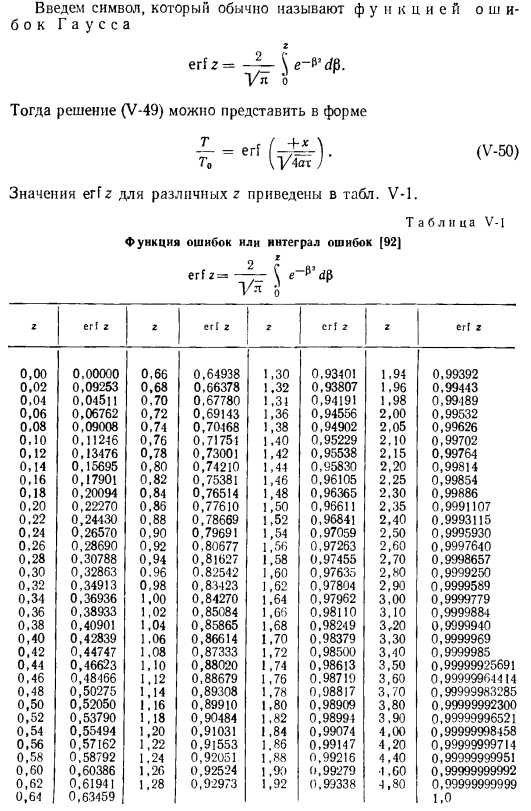
Перепишите (V-48) в соответствии с 233 ’2’2 — = 2 pl 233’2’2 в виде: (V-49) Является функцией верхней границы. Уравнение (V-49)является искомым solution. It вводит символ, обычно называемый f u и k c. речь идет о erf z = — Str b на Гауссовой стороне w. Тогда решение (V-49) Может быть выражена в виде (V-50).Различные значения G erf z приведены в таблице. Фау-1.
Таблица V-1 функция ошибки или интеграл ошибки[92] erf2 — \ e Y * o g erf g G erf z SGG 2 2 2 erf з. 0.00 0.00000 0.66 0.64938 1.30 0.93401 1.94 0.99392 0.02 0.09253 0.68 0.66378 1.32 0.93807 1.96 0.99443 0.04 0.01511 0.70 0.67780 1.31 0.94191 1.98 0.99189 0.06 0.06762 0.72 0.69143 1.36 0.94556 2.00 0.99532 0.08 0.09008 0.74 0.70468 1.38 0.94902 2.05 0.99626 0.10 0.11246 0.76 0.71751 1.40 0.95229 2.10 0.99702 0、 12 0.13476 0.78 0.73001 1.42 0.95538 2.15 0.99764 0.14 0.15695 0.80 0.74210 1.44 0.95830 2.20 0.99814 0.16 0.17901 0.82 0.75381 1.46 0.96105 2.25 0.99854 0.18 0.20094 0.84 0 76514 1.48 0.96365 2.30 0.99886 0.20 0.22270 0.85 0.77610 1.50 0.96611 2.35 0.9991107 0.22 0.24430 0.88 0.78669 1.52 0.96841 2.40 0.9993115 0.24 0.26570 0.90 0.79691 1.54 0.97059 2.50 0.9995930 0.26 0.28690 0.92 0.80677 1.56 0.97263 2.60 0.9997640 0.28 0.30788 0.94 0.81627 1.58 0.97455 2.
70 0.9998657 0.30 0.32863 0.96 0.82542 1.60 0.97635 2.80 0.9999250 0.32 0.34913 0.98 0.83423 1.62 0、 97804 2.90 0.9999589 0.34 0.36936 1.00 0.84270 1.64 0.97962 3.00 0.9999779 0.36 0.38933 1.02 0.85084 1.65 0.98110 3.10 0.999988 * 1 0.38 0.40901 1.04 0.85865 1.68 0 98249 3r20 0.9999940 0.40 0.42839 1.06 0.86614 1.70 0.98379 3.30 0.9999969 0.42 0.44747 1.08 0.87333 1.72 0.98500 3.40 0.9999985 0.44 0.46623 1.10 0.88020 1.74 0.98613 3.50 0.99999925691 0.46 0.48466 1.12 0.88679 1.76 0.98719 3.60 0.99999964414 0.48 0.50275 1.14 0.89308 1.78 0.98817 3.70 0.99999983285 0.50 0.52050 1.16 0.89910 1.80 0.98909 3.80 0.99999992300 0.
52 0.53790 1.18 0.90484 1.82 0.98991 3.90 0.99999996521 0.54 0.55494 1.20 0.91031 1.84 0.99074 4.00 0.99999998158 0.56 0.57162 1.22 0.91553 1.86 0.99147 4.20 0.99999999714 0.58 0.58792 1.24 0.92051 1.88 0.99216 4.40 Определение 0.99999999951 0.60 0.60386 1.26 0.92524 1.90 0.99279 4.60 0.99999999992 0.62 0.61941 1.28 0.92973 1.92 0.99338 4.80 0.99999999999 0.64 0、 63459 1.0 потребления тепла.
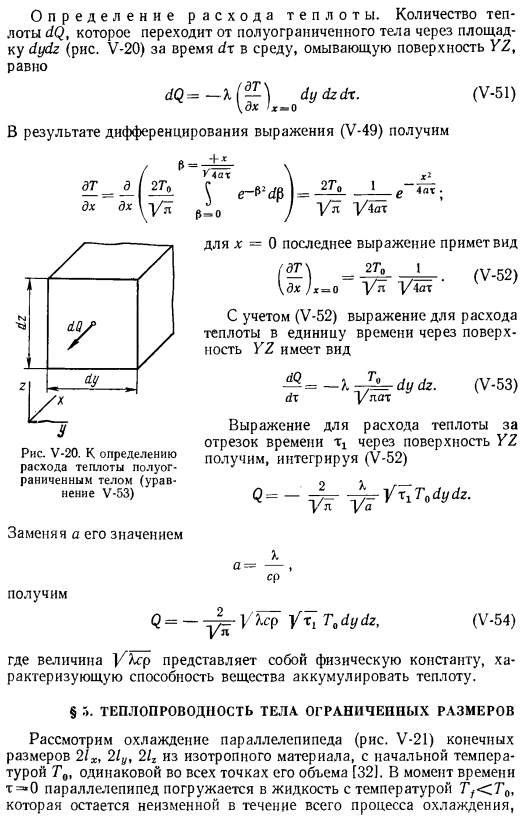
Количество тепла DQ, поступающего в среду для промывки поверхности YZ путем прохождения через платформу dydz (рисунок V-20) от полуограниченного объекта в течение времени dr в результате дифференциала Возвращает выражение (V-49). 4-х / Y4ax \x1dx ДХ \ г ^ₚJQ / уя УАТ в-20.Для определения расхода тепла полуограничивающим телом (формула V-53) заменить а на значение Х = 0 Последнее выражение принимает вид (V-52).Формула для теплопотребления в единицу времени поверхности YZ имеет вид^ = — K — ^ dydz. (V-53) dx Y L в уравнении расхода тепла .
Получим Интеграл (V-52) cp-Ydydz, (V-54) для временного интервала tx через поверхность YZ, чтобы получить. Значения характеризуют способность физических констант Вещество накапливает тепло. § 5.Рассмотрим охлаждение параллелепипеда (рис. V-21) конечного размера 2 / x, 2ly, 2lz из изотропии теплопроводности объекта ограниченных размеров.
Материал начальной температуры, то же самое[321 во всех точках его volume. At время t = » 0, параллелепипед погружен в жидкость с температурой TfT₀. При этом не изменяется на протяжении всего процесса охлаждения и коэффициент теплопередачи А. При таких условиях температурное поле симметрично относительно центра параллелепипеда. Поставь Происхождение есть.
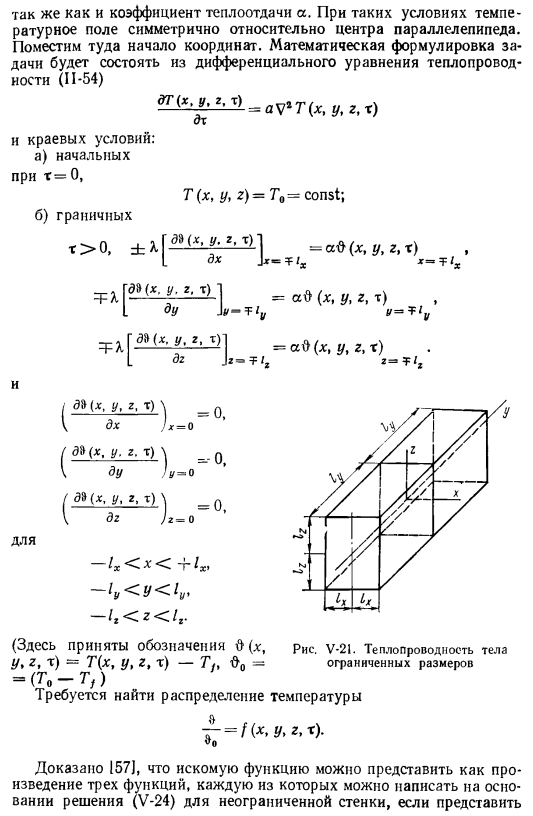
Математическая постановка этой задачи основана на дифференциальном термическом уравнении (P-54)^(*dtATLₑV. T (W, t) состоит из dx и граничных условий. Р = 0. T (x, y, z)= To = const; b)границы t> 0,= a $(x, y, r, r)m / xx g^1xdx 38(X, y, 2, m)j 38 (x. u. 2, m)i du = FX GE8(x, y, 2, t) 1 L d2 и/ e»(X, y, ’•T) ’ | −0. к ДХ / х = 0/38 (x, y. gtP-0.1 du / / = 0 /(x, y. g ’ t) ’| −0.to dg A = 0 для-lₓX+lₓ, — lyylᵥ.на корме (x, y, z, t) АО (x, y, z, r) рисунок V-21.Теплопроводность объекта ограниченных размеров (принимается здесь) .
Обозначения О(х, ууг, т)=Т(х, у, з, т)-Tₕ—(T₀-ТФ)распределение температуры, чтобы найти нужную—= ф (х, Г, З,-С). «O 157J доказал, что искомая функция может быть выражена в виде: Продукт 3 функций. Если поле представляется как пересечение 3 таких стенок, то каждая из них может быть записана на основе неограниченного решения стены (V-24). Формат нужной функции-0 _ (х, т) 0(у.0 (z, т)•V-55) * Vo-это V0o. Oo O (X t) O (Y, t) 0 (z, t)O’o o’o OO-распределение температуры в неограниченной плоскости YZ、 XZ, XY.
Формой решения рассматриваемой задачи на основе (V-55) и (V-24) является/ + Pm. y, PVz 12y’h(V-56), где Aᵢₜx, am > y-коэффициенты ряда решений (V-25) соответственно. Если ограничиться только первыми членами (V-35) строки: 0 (x, t) и Bi =y-Zₓ, а также (y, t) и Bi = y-1y, 0(z, t) и Bi = y / Z. формула (V-56) значительно упрощается и принимает вид коэффициентов коэффициентов. ЛtheХ, Л₁₂, и характеристическое уравнение Пи, х, Р₁>у, Pᵢₜz корней, потребление тепла, чтобы определить из графика каждого может быть определена (рисунок V-12 и V-13 справки).
Теплопотребление каждый кубический метр материала параллелепипеда за время от m-0 до m-m (см. Рисунок V-21) определяется по формуле: Q — cf [- &₀- 0(m) 1, 0 ® — средняя температура Tx ly LZ e w = JJ Ji $ Y определяется из соотношения параллелепипеда в конкретной точке m = m. 2, x) dxdydz. (V-58) ’ x ’ y ’ zooo уравнение для усреднения При температуре 0 (t) в определенный момент времени tx значение d (x, y, z, t) из (V-58) получается путем подстановки (V-58) Oo 1X1 y x (V-59) коэффициентов Bᵢₓ, Bₗₜ y, Bᵢₜg и корня. Характерные уравнения₁жж, л, у, P1.Z можно определить из графика соответственно (см. Рисунки V-12 и V-15).
Смотрите также:
| Метод обобщенных переменных | Приближенные методы решения задач теплопроводности |
| Теплопроводность при стационарном режиме | Исследование теплоотдачи методами теории пограничного слоя |

