Оглавление:






Теплопроводность плоской стенки при двумерном температурном поле
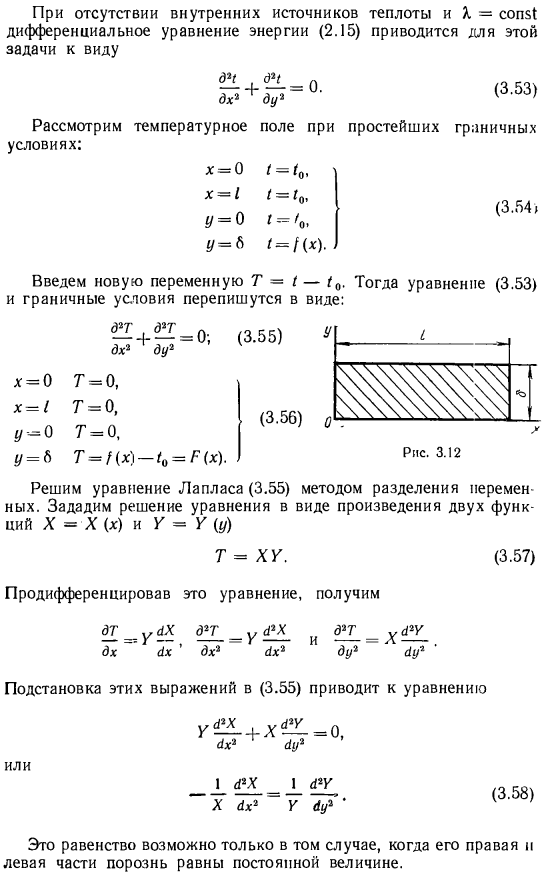
- Проблема теплопроводности, рассмотренная выше, является довольно простым решением, потому что все это сформулировано для 1-мерной температуры field. In на практике, когда температурное поле становится 2-D или 3-D, проблема возникает в более сложных граничных условиях. В качестве примера рассмотрим теплопроводность пластины в 2-мерном поле температуры (рис. 3.12). 2-мерность температурного поля пластины возникает между изоляцией края пластины перпендикулярно оси z и равномерностью условий теплообмена вдоль этой оси.
Внутреннего источника тепла нет, и уравнение K = const (дифференциальное уравнение энергии (2.15) сводится для этой задачи к следующему виду: (3.53) Рассмотрим Температурные условия. Самое простое поле-это граница. х = 0 х = 1 Y = 0 г = 6 (3.541 Введем новую переменную T = i-1″.Затем перепишем формулу (3.53) и граничные условия в следующем виде: Решите уравнение Лапласа (3.55), используя метод разделения переменных. Определим решение уравнения в виде произведения 2-х функций X = X (x) и Y = Y (y Т = СЮ. (3.57) Если продифференцировать это уравнение、 Ых ДХ ’1hg Даг Лу . Это приводит к уравнениям.
На расстоянии йх это количество тепла изменяется на величину Таким образом, количество тепла, уходящего из элемента объема через плоскость 3— 4, больше количества тепла, поступающего через плоскость 1 — 2, именно на эту величину. Людмила Фирмаль
Замена этих представлений 1 РХ _ _1_ азу xah1〜г //У1 ’ (3.58) Эта однородность возможна только в том случае, если ее правая и левая части по отдельности равны постоянной величине. Указывает константу разделения переменных в p’.Тогда из Формулы (3.58) можно увидеть следующее: — +zrX-0, (3.59) — Пи! Г = 0.(3.60)) Решение этих уравнений выглядит следующим образом: Х = = С1 сов РХ + с, 81n Военторга Y =С₈ «» » + € е -«.
Итак, согласно формуле (3.57), общее решение будет иметь вид: Т =(СГ СРХ + с, 81p пикселей) (СП + СК — — -). (3.61) Интегральная константа этого уравнения определяется на основе граничного условия (3.56). у = 0 условие 7 = 0 удовлетворяется в случае СГ = — к. для того, чтобы равенство 7 = 0 провести х = 0, оно должно быть C₁= 0.условие 7 = 0 для x= I должно быть p = y(n = 1, 2, 3…
- Исходя из Формулы (3.61), с учетом найденной интегральной константы можно записать бесконечное число частных решений формулы(3.55).Общее решение этого уравнения можно записать как сумму некоторых решений = 2 2spv11-присоединиться| Н22-х、 (3.62) Гиперболический синус (3.63) решение, соответствующее * n = 0, тривиально. Это имеет место для атома, если значение аргумента 7 = 0.Поэтому он исключается из рассмотрения. Последняя константа-C». Граничные условия используются для определения Если вы назначите его формуле (3.62)、 Куда? G (x) «2 2С» 5Ь22-6$1п 2рр-х= = 2 Л » 8ШУХ、 Л «=2С » 5Ь-6.
Выражение (3.64) является разложением функции P (x) в ряд Фурье синуса (предполагается, что такое разложение возможно).Коэффициенты этого разложения определяются по известной формуле Л » = г? (х) Вит ух 4х. (3.66) Если сравнить уравнения (3.65) и (3.66)、 ЦН = — — — — — — С Р(х) 8Ш-х 1х. (3.67) ЙОРК’- Учитывая это уравнение, уравнение (3.62), определяющее рассматриваемое температурное поле, сводится к окончательному виду.
При расчете опять можно ограничиться двухмерной задачей, приняв свойства жидкости постоянными, а скорости настолько малыми, что увеличением температуры, обусловленной внутренним трением в пограничном слое, можно пренебречь. Людмила Фирмаль
Здесь мы рассматриваем ту же задачу при более сложных граничных условиях: мы предполагаем, что 2 конца пластины изолированы, а остальные 2 поверхности характеризуются произвольным распределением температуры. х = 0 (3.69)) г = 0 Решение дифференциальных уравнений для этой задачи остается прежним(здесь полезно оставить переменную I без замены) Я =(с, Потому что РХ + с, СС ПХ) (с,+C₄e-Н»), (3.70) Результат. = П(С, потому что ПКС-с, 81n пикселей) (С2 + С, Е -^.(3.71)) поскольку x = 0 и dNdx = 0, условие для C»= 0; x= 0•= /выполняется в случае p=.Где: n= 0、1、2、3…(Где n = 0 не является простым решением). Представляет типичное решение как сумму данного решения ’=/+ı2«.
Учитывая интегральную константу выше VDGP = разрыв. (3.73) если n = 0, то из формул (3.59) и (3.60): X₀= Ах + ViY₀= Ой + Н Так… «О-Х» Г₀■=(Ох + Е) (ТИЦ + Ч). (3.74) Величина, определяемая формулой (3.72) для того, чтобы dIdx был равен нулю при x = 0, требует условия/₀^ *φ (x). таким образом, O = 0 и уравнение (3.74) можно переписать в виде: ’o-Lo1 / +B₀. (3.75) Подставляя уравнения (3.73) и (3.75) в уравнения (3.72)、 ’=₀₀(/4-B₀ + 2(е «E1 *» + bn- > 1*) co8 (1x. (3.76)) Согласуйте оставшиеся 2 граничных условия для этого решения. Подставляя эти условия в (3.76) и принимая во внимание формулу p, получаем формулу: s (х)= БО + 2 ООН + БН) потому что-Х.
Если мы сравним эти выражения с теми, которые расширяют функцию ряда Фурье Косинуса, мы увидим следующее: — т и Л, 1₊л,=±рил; Обезьяны ’+ Bee1=-§/(х) ГП-1х. Эти 4 формулы позволяют рассчитать коэффициенты A₀, ₀₀, an и BP. Найденное таким образом распределение температуры позволяет определить тепловой поток, проходящий через поверхность рассматриваемых пластин или элементов этих поверхностей. Таким образом, локальная плотность теплового потока к нижней горизонтальной плоскости пластины (рис. 3.12) определяется по формуле При 3 — ⁷⁹ » градиент температуры рассчитывается по формуле (3.76) или (3.68).
Смотрите также:
| Контактное термическое сопротивление | Условия подобия температурных полей при нестационарной теплопроводности |
| Теплопроводность тел с внутренними источниками теплоты | Результаты аналитического решения |

