Оглавление:




Теплопроводность цилиндрической стенки
- Рассмотрим теплопроводность однородной цилиндрической стенки большой длины, так что передача тепла из грубо конце можно пренебречь (рис. 3.6). Если внутреннюю и внешнюю поверхности поддерживать при постоянной температуре, то тепловой поток будет идти в радиальном направлении, а изотермическая поверхность будет иметь форму цилиндра. В этих условиях температурное поле I имеет размерность 1. Используйте радиус r, r и длину I для оценки размеров стены и предположите, что теплопроводность одинакова для всей стены.
В случае стационарной 1-мерной задачи теплопроводности цилиндрической стенки без внутреннего источника тепла дано дифференциальное уравнение энергии, учитывающее (2.16: 0. (3.18) Введение новых переменных (3.19) Формула (3.18) может быть сформирована (3.20 утра)) После разделения переменных и интегрирования получаем 1Н и+ 1П Р = 1П с (3.21) Если мы усилим это выражение и переместим его в исходную переменную и интегрируем его、 1 = СГ 1П г + с*. (3.22) Таким образом, зависимость I = I (g) имеет логарифмическую природу (рис.3.6). Кривизна тепловой линии стенки цилиндра обусловлена изменением плотности теплового потока с изменением радиуса цилиндра.
Требуется рассчитать толщину ламинарного пограничного слоя и коэффициент трения при обтекании плоской плиты в случае приближения кривой распределения скоростей к прямой линии или к параболе. Людмила Фирмаль
С меньшим радиусом, площадь поверхности, через которую проходит тепло также decreases. So, в малом радиусе температурная линия движется более резко. Это правило действует и в противоположном направлении теплового потока (пунктирная линия на рис. 3.6). Граничные условия типа 1 описываются уравнением. Подставляя эти выражения для равенства (3.22), вы получаете: Если заменить интегральную постоянную формулы (3.22) на Формулу (3.23), то получим уравнение температурного поля. 1= -, (3.24) Где А, а внутренний диаметр цилиндра 1 1 L — — — ne- Диаметр ремня. Тепловой поток через изотермическую поверхность с радиусом можно оценить по закону Фурье.
- Из уравнения (3.24) получим следующее уравнение для градиента температуры: Начальное тепловое сопротивление цилиндрической стенки. Плотность теплового потока внутренней и наружной поверхностей7 и2.С = Q, я = Q, а ЖЖ] я = 4г НР! Г1、 4,= л д, д,= л-е% д%. Эта формула может быть использована для вычисления q или q относительно q. — При2, то есть если стенка трубы тонкая, то кривизна стенки будет незначительно влиять на величину теплоты flux.
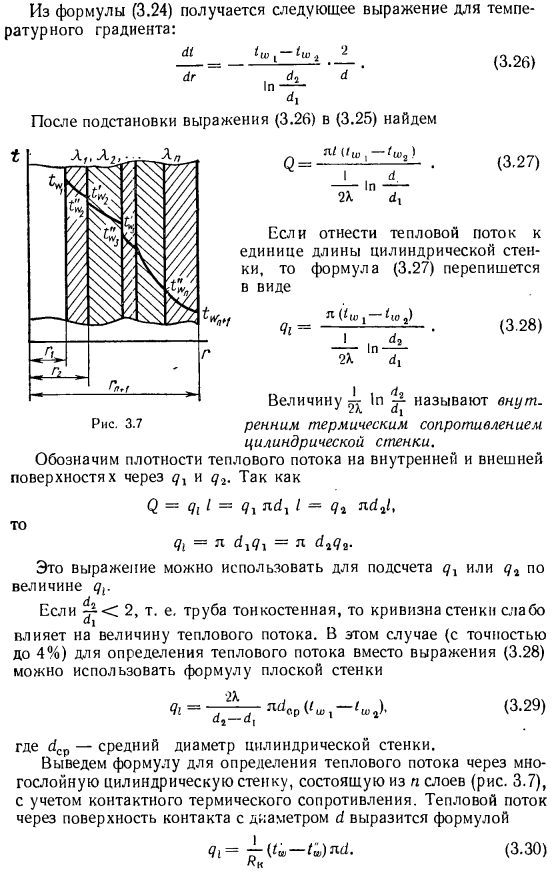
В этом случае (точность 4%) вместо формулы (3.28) можно использовать формулу плоской стенки для определения теплового потока. (’Вт>»’»,»)• (3.29) Здесь 4С-средний диаметр цилиндрической стенки. С учетом контактного теплового сопротивления выведена формула для определения теплового потока через многослойную цилиндрическую стенку, состоящую из n слоев (рис.3.7).Тепловой поток через контактную поверхность диаметром 1 выражается в виде: В устойчивом режиме количество. Одинакова для всех участков теплового тракта. Их можно определить по формулам (3.28) и (3.30).
Сходство в граничных условиях на внешнем крае пограничного слоя требует, чтобы градиент давления др)дх для осесимметричного потока был идентичен градиенту давления др)дх для двухмерного потока. Людмила Фирмаль
Явным образом выразите разницу температур из этих уравнений и суммируйте левую и правую части уравнения после перестановки членов.(3.32). Если контактное тепловое сопротивление можно игнорировать, то в уравнении (3.32). Температура поверхности отдельных слоев определяется по формуле, выведенной таким же образом, как и для плоских стенок. Таким образом, для оценки температуры Г формула принимает вид: Температурное поле многослойной цилиндрической стенки показано на рисунке.
Смотрите также:
| Теплопроводность плоской стенки | Теплопередача через цилиндрическую стенку |
| Теплопередача через плоскую стенку | Контактное термическое сопротивление |

