Оглавление:





Теплоотдача плоской пластины при постоянной температуре поверхности
- При определении количества тепла, отводимого от пластины M не учитывают тепло трения, поэтому учитывают скорость, при которой тепло очень мало. Трение по сравнению с количеством тепла, переносимого конвекцией, не играет роли. В соответствии с этим дифференциальные уравнения описываются в следующем виде: Следующие граничные условия: если y = 0: — ww = 0, — ww = 0, 0 = 0 ^(постоянная температура поверхности пластины); если y = co*. / W = M7 (скорость свободного течения), 0 (температура не возмущена). Чтобы решить эту систему уравнений, сначала Эта «функция тока * φ (x, y)» явно удовлетворяет уравнению непрерывности.
Затем член вводится как новая переменная Итак, для начальной переменной,、 Теперь граничные условия для C и 0 являются: В этом случае 3 исходных дифференциальных уравнения в частных производных преобразуются в 2 обыкновенных дифференциальных уравнения Стандарты пристол. Функция C (5) была впервые определена Blasius1.Зная это, можно записать решение преобразованного уравнения энергии (89) в виде: Теперь нам нужно назначить его в соответствии с граничным условием 0 = 1 = y = 5 = oo Таблица 4 Коэффициент теплопередачи продольно обтекаемых пластин функция fx (Pr) (по Полхаузену) Критерий В таблице. На рис.
Однако изменение темпер ату- ры в ту или иную сторону невозможно согласно второму закону термодинамики, по которому никакие температурные различия не могут возникнуть самопроизвольно в замкнутой системе, когда она находится в состоянии теплового равновесия. Людмила Фирмаль
Показано значение этой функции/ x (Pr) путем вычисления порхаузеном числа Прандтля Pr = 0,6-15.Эти числа могут быть аппроксимированы с соответствующей подгонкой. Зависимость Его применение возможно примерно до Pr = 1000.Температурный градиент стенки определяется по формуле (90) в следующем виде: Также можно определить количество тепла, выделяемого с одной стороны пластины на единицу ширины Где а представляет собой локальное значение коэффициента теплопередачи.
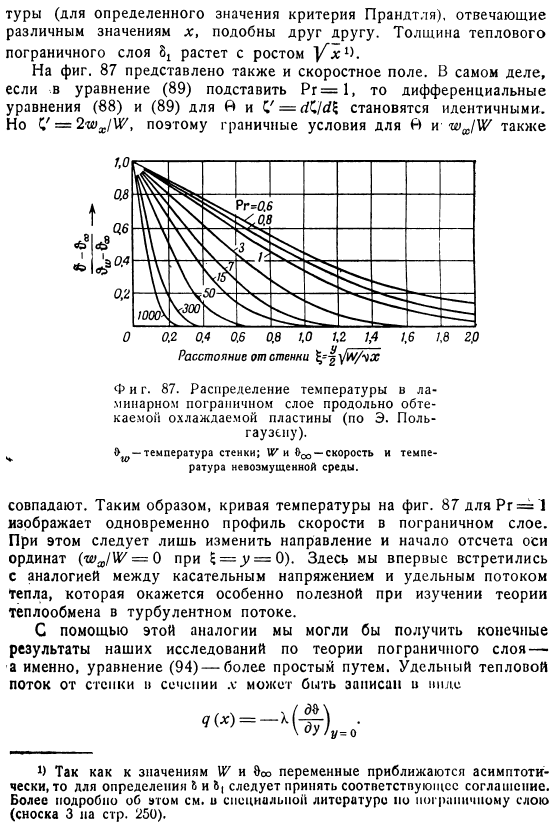
Из текущих значений a и x отсчитайте от начала пластины, Если вы хотите построить ссылку Li、 Из уравнений (92) и (93) Кроме того, здесь, Кеа=нет. gx / y-это норма скорости набегающего потока и текущего общего количества тепла, передаваемого от секции к стенке секции X. В качестве неотъемлемой Ре X значение изображения. Начало Теперь можно создать среднее значение критериев нуссельта в форме Оба значения критерия Нуссельта справедливы при условии одностороннего теплообмена. 1 87, решение уравнения (90), 1 = 0 =(0-1>ω)/(0 «-&»)$ == y / 2 ″ Um / / представлен в виде кривой, определяющей величину, зависящую от uh.
Ордината-это относительная избыточная температура (по сравнению с температурой нестемпфированного потока), которая приводит к полной разнице в температуре и температуре между стенкой и невозмущенной температурой. Поток. Это температурное поле позволяет прояснить некоторые существенные особенности механизма теплопередачи в ламинарном потоке. На стене ($ = y = 0) она равна CHOA и нулю、 Итак, здесь, согласно формуле (87), q2 / q2 = 0 также должно присутствовать. Это означает, что существует линейное распределение температуры в результате чистой теплопроводности.
- Больше, чем Чем больше значение критерия Прандтля, тем круче наклон температурной кривой, и поэтому толщина температурного пограничного слоя и профиля темперамента меньше? Соответствующие различным значениям x(конкретные значения критериев Прандтля), похожи друг на друга. Толщина теплового пограничного слоя увеличивается с увеличением На рисунке 1 87 также показана скорость field. In дело в том, что если подставить Pr = = 1 в уравнение (89), то дифференциальные уравнения для A и C (88) и (89) То же самое. Расстояние от стены F и D. 87.Распределение температуры ламинарного пограничного слоя продольно охлаждаемой пластины (E.
Температура стенки. И / или ООО-скорость и температура среды без возмущений. Матч. Таким образом, температурная кривая на фиг. 3, Pr = 1 из 87, показывает профиль скорости пограничного слоя в то же время time. In в этом случае вам просто нужно изменить направление и начать Ссылка на вертикальную ось (если 5 = ^ = 0, ТО^ / 1 ^ = 0).Здесь мы впервые описали сходство касательных напряжений и удельных тепловых потоков. Изучается теория теплообмена в турбулентных потоках. Используя эту аналогию, можно было получить конечный результат исследования по теории пограничного слоя, то есть уравнение (94), более простым способом.
Действительно, в вакууме или системе, находящейся в состоянии теплового равновесия, тело 1 может обмениваться теплом с окружающей средой только путем излучения. Людмила Фирмаль
Удельная теплоемкость Поток от стенки поперечного сечения x может быть записан пилой Variable переменная асимптотически приближается к значению # и 8°, поэтому для определения&необходимо принять соответствующее соглашение. Дополнительные сведения см. В разделе Специальные Литература по пограничному слою (сноска на стр. 2503).
Напряжение сдвига стенки с таким же поперечным сечением выглядит следующим образом Если вы почти принимаете линейный закон распределения скорости и температуры пограничного слоя и устанавливаете толщину обоих пограничных слоев одинаковой($ = op, Pr-1 Вы получите следующие зависимости: Понятие местного значения нуссельта справочник ли = ох / л = 7(х) * х / \(0 ^-ООО) и ссылка Рейнольдса Ке ^ = Р: ц / хр / М] = Г / Х / ^можно переписать полученное уравнение В форме Гидродинамическое решение пограничного слоя 1> При условии одностороннего теплообмена от пластины вида: найти локальное значение числа N11.
Этот результат Pr = 1 соответствует выражению (94).Однако результаты точного решения полхаузена согласуются с приближенными оценками, так как оба поля являются Температура и скорость-считались одинаковыми. Предпосылка 3 = $! Поскольку предположение Pr = I уже сделано, оно приведет к тождеству дифференциала. Уравнение 8 и с(88) и (89).Но с другой стороны, это возможно только в том случае, если градиент давления 7p x очень мал, как это происходит, когда он действительно течет Тарелка.
Тоже фигура. Кроме того, 87, можно оценить толщину пограничного слоя 3 для поля скорости и поля температуры. Если Pr = 1, то пограничный слой соединяется, в результате чего получается 3 = o1.Из рисунка Приближенная зависимость 3/31 = Pr / a.
Смотрите также:

