Оглавление:









Теплоотдача конечной интенсивности (граничные условия третьего рода). Пластина
- Бесконечно большая параллельная плоская пластина толщиной в 2 раза передает тепло с 2 сторон в окружающую среду. Коэффициент теплопередачи с обеих сторон одинаков, равен a. температура окружающей среды B равна нулю на обеих сторонах sides. In время 1 = 0, пластина имеет одинаковую температуру везде 0 = 0 seconds. In кроме того, сделайте физические константы пластин X, c, o и, таким образом, постоянными. Наконец, оставьте относительный коэффициент теплопередачи A = a / X неизменным, как well. It необходимо определить вид температурного поля и величину теплопотерь в зависимости от времени а) математическая постановка задачи.
Рассматриваемая задача отличается от задачи введения только тем, что начальная температура 0С не изменяется вдоль оси Х и остается неизменной constant. In в этом случае мы приходим к следующей математической постановке задачи. Дифференциальное уравнение 61-A dhg ’ Пространственные граничные условия икс.- \- =Х — ЛО、 для Х = — Х; Временные граничные условия для 1 = 0 0 = 0c. P) определение температурного поля. Мы уже знаем, что дифференциальное уравнение имеет следующий частный Интеграл. 0 = Ce-t’a181n(tx) и 0 = ye-n’A1 cos (nx).
Следовало ожидать, что для больших чисел Рейнольдса (и соответственно для больших скоростей потока) и малых чисел Грасгофа влияние свободной конвекции на перенос тепла может не приниматься во внимание. Людмила Фирмаль
Начальное распределение температуры симметрично относительно плоскости Y-2, но поскольку температура окружающей среды и коэффициент теплопередачи одинаковы с обеих сторон пластины, такая симметрия должна поддерживаться на протяжении всего процесса выравнивания температуры. Поэтому функция температуры может быть только четным числом, поэтому первый частичный Интеграл может быть исключен из consideration. To сопоставив оставшиеся интегралы с условиями поверхности, необходимо правильно выбрать значение n в уравнении (пх) 51n (пх)= {НХ) потому что {пх). Корни этого уравнения ok = {pkX) известны и сведены в таблицу. 2.
Из множества конкретных решений, полученных таким образом, построим общее решение вида: Л = ОО Б = ^ ОК ПК°1 в COS (ПХ). Значение Ok должно быть определено для удовлетворения начальных условий Да. $ C = ^ OkC03 (PkX). Однако эти значения можно найти из Формулы (156). Г0сСО5 (ллх)^ X 2 5111 {PX) в соз2 (ПХ) ЛХ О_________ *)________ С 51p позволяют вести съемку быстро (pkX) соѕ(pkX) 4-(pkX)* {стр.
Введение в нотацию КХ).Получаем функцию температуры в виде уравнения L = 1 (24а) Один Значение B *в этом уравнении является корнем уже упомянутого трансцендентального уравнения, параметры которого равны только HX. Следовательно, величина самого bk также должна быть функцией этого параметра. Поэтому(246) Уравнение(24а) можно представить в виде ^ =Ф(ЛХ,^ _ Это уравнение представляет собой важный момент.
Несмотря на то, что задачи, налагаемые физическим содержанием, зависят от очень большого количества отдельных величин, эти величины можно сгруппировать таким образом, чтобы они в конечном итоге получили функции, зависящие только от 3 аргументов. Он также описывает конкретный случай, когда величина а принимает неограниченное значение, то есть когда температура поддерживается на нулевом уровне на обеих поверхностях. Тогда o (см. стр. 50) соответствует значению аргумента нулевой точки косинусной функции. То есть, он получает значение. Знак этих значений аргументов всегда 4-1 или −1.Формула (24) принимает вид: Я — (24 то) к)графическое отображение температурного поля.
В основе анализа лежит конкретный случай, то есть бетонная стена толщиной 2X = 80 см, а температура стенки Ps и перепад температур при температуре окружающей среды= 0 до 1°.Для другого числа вам нужно только выбрать соответствующую шкалу для оси температуры. Коэффициент теплопередачи А составляет 10,8 ккал! М2 * * час-град. L такие результаты могут быть получены без непосредственного решения дифференциальных уравнений с использованием метода теории подобия, как показано более подробно в части 2 книги. — Примечание автора * ) Формулу LX = aX / X без измерений следует отличать от числа нуссельта N11 = aX / X^, которое будет введено later.
Первое выражение, X представляет теплопроводность твердого тела, а в числе нуссельта, X ^представляет окружающую среду. Заметим, что более глубокое и фундаментальное различие между этими двумя уравнениями состоит в том, что первое уравнение рассматривает коэффициент теплопередачи как известную величину, заданную условиями, в то время как второе уравнение рассматривает неизвестную величину, которая должна быть точно определена. — Примечание Издание 1.Предварительный расчет. Конкретно из таблицы найти X = 0,6 ккал / М * время * город\ Р = 2000 кг! м * \ с = 0,27 ккал! кг * град. И затем… а =-= 0.0011 мг (среднее время м Λ= y =—= 18,0 м-1 и Λ= 18,0 * 0,40 = 7,2.
Значение определяется из состояния поверхности. Корень трансцендентального уравнения 6 * =(/цХ) взят из таблицы. (LH)= 7,2 в качестве промежуточного значения 2.Первые 5 маршрутов суммируются в таблице. Один. Таблица А * = 1 L = 2 l = s L = 4 Радиан. 1.38 4.18 7.08 10.03 13.08 ** 79°6 ’239°30′ 45°27 ’214°54′ 29°13 ′ Что вам нужно больше: 51p позволяют вести съемку быстро 0.9820 −0.8616 0.7127 −0.5722 0.4882 потому что 0.1891 −0.5075 0.715 −0.8202 0.8744 3.Характеристическое решение A (x) = cos(/?Lx) = cos-y). чтобы выделить эти решения, установите положение нулевой точки, а также положение максимума и минимума, например 1-го, 2-го.
Если первый ноль соответствует значению x0, то конечная нулевая точка находится в 3×0, 5×0,7×0 и т. д. Минимальное значение находится в точках 2×0,6×0, 10×0, а максимальное — в точках 0,4×0 и 8×0. Первая нулевая точка исходит из условия Поп-Щ)= 0 = поп-г Мэри. −2. х ’ Л1 ′ оло°> 628• * о-2″ = В * = С х0 2×0…Расчетное значение (в метрах) приведено в таблице. Б. Таблица Б L = 1 L = 2 L = 3 L = 4 L » 5 1.Пули х ^ 0,455 0,151 0,089 0,063 0,18 Мин 2 * 0-0. 301 0.178 0.126 0.096 2.Нулевая Точка 3 * 0-0.
- Нулевая точка равна 9 * 0 0.432 4. Определите приблизительный коэффициент. Из уравнения 0 _________2 $ 1П(кривых)_______ к (pkX)+ 51p позволяют вести съемку быстро (pkX) соѕ(pkX)• Используйте данные в таблице. Б, мы получим Р1 = + 1.250; Г> 2 = −0.373; Р3 = 4-0. Сто восемьдесят восемь; =-0.109; = + 0.072. 5. расчет величины е*. Рассмотрим 2 случая: I = 0 и I = 5 часов. Случай 1. Если / = 0, то экспонента гасится и экспоненциальная функция гасится.
Значение, вычисленное в разделе 4, является характеристическим решением, поскольку оно дает амплитуду функции co-y ^ = D (x). Случай 2./ = Значение 5 часов. — Подходящий = 0,0344.Уберите отсюда стол. Б. Таблица B L = 1&= 2 * = 3 L » 4 М — * Л1 0.0655 0.601 1.725 3.465 5.885 Экспоненциальная функция 0.94 0.55 0.18 0.03 4-1. 175 −0.203 4-033 −0.003 0 6.Графическое отображение температурного поля. 1. Начальное распределение температуры ^ = 0 получено из следующего расчета: 〜= {1,250 Кос(3.45 х) −0.373 потому что(10.4 х) 4 4-0.Поп-188 (17,7 х) −0.109 поп(25.1 х) 4 4-0,072 Кос(32,7 х) — 4- ..) = = {1-П + Ш-1У + У-4.}.
В дополнение к числам Рейнольдса и Прандтля существенными являются число, Грасгофа, а также параметры, описывающие геометрию границ и ориентировку потока относительно гравитационного поля. Людмила Фирмаль
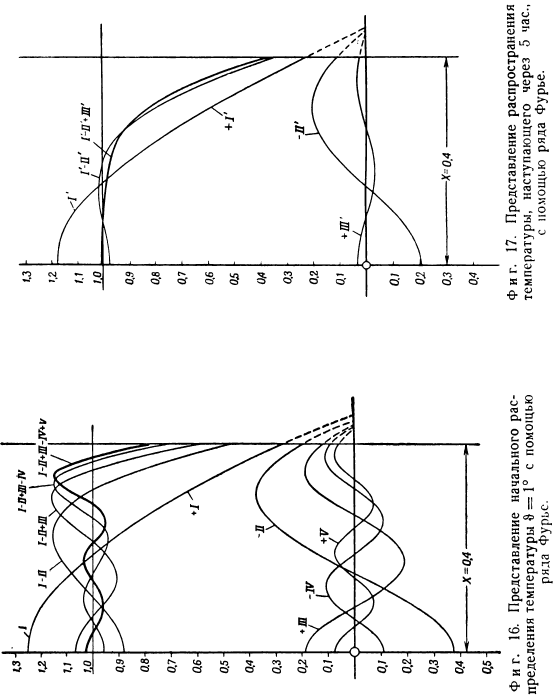
В последнем выражении I, II следует понимать как индивидуальные конкретные решения.1. как показано на рисунке 16, эти решения представлены индивидуально и в виде алгебраических уравнений. sums. It видно, что первое частное решение существенно отличается от начального распределения температуры: 0c = sfc = 1°.Однако в то же время нетрудно заметить, что чем точнее воспроизводится исходное распределение, тем более конкретные решения накладываются друг на друга. Но в то же время 5 конкретных решений недостаточно, чтобы точно представить распределение графически. При последующем распределении температуры условия значительно улучшаются improved. So переходим ко 2-му распределению. 2.
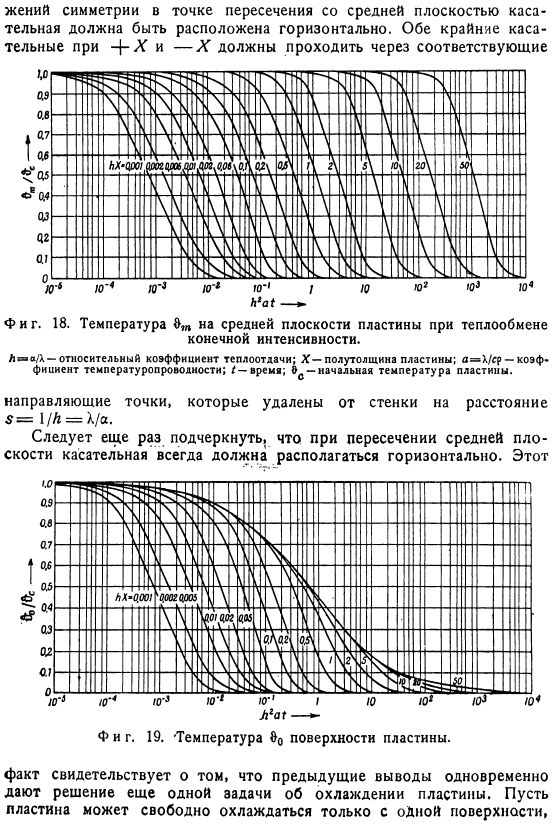
Распределение температуры в 1= 5 hours. It получается из следующих расчетов: — =(1.175 поп (3.45 х) поп −0.203(10.4 х) 4 4 0.033 soz (17.7 x) −0.003 cos (25.1 x)= + = 0} = {I ’- II ’4 III ’ — IV’). Как видно из расчетов, для точного определения температуры достаточно лишь 3 или 4 членов ряда. Рисунок 1 на рисунке, как и прежде, показаны как отдельные конкретные решения, так и сумма χ.Из рассмотрения рисунка, вы можете увидеть его через 5 часов. Хотя только самый внешний слой стенки значительно охлаждается, а внутренний слой почти полностью сохраняет начальную температуру в、 7.Упрощенный графический дисплей.
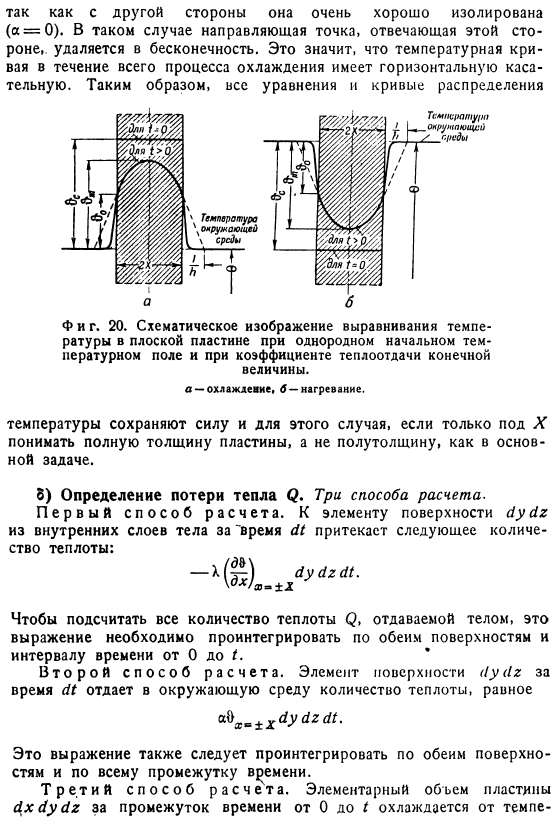
При решении технических задач, как правило, не нужно знать, как строится вся температурная кривая из этого конкретного solution. In в большинстве случаев достаточно ли распределить значение температуры центральной поверхности пластины и температуру Lo обеих из них вверх? Новости. Чтобы определить температуру промежуточной поверхности, установите x = 24 в формуле (0) и получите (25а) Чтобы определить температуру поверхности, то * =X. (256) В отличие от функции to выражения (246), функция и Фзависят только от 2 независимых переменных. Поэтому при необходимости их можно отобразить в виде таблицы или рисунка.
При фактическом использовании таких диаграмм неудобно как для переменных функций Фт, так и для variable включать половину толщины пластины X. Поэтому мы предпочитаем использовать форму выражения температуры на промежуточной плоскости o, предложенную Бахманом X> ^ = Хм (КХ, / Хаг)(25С) Я Температура наружной поверхности ^ = Xa (HX, N’AG). (25г) Новая (безразмерная) переменная берется как произведение (LX) 2•o // X2 = A2o/.Формулы (25c) и (25G) показаны на фиг. 18 и 19, согласно новому расчету Бахмана. Для некоторых задач (в этом случае a и A считаются постоянными) абсцисса пропорциональна времени/; * параметр равен половине толщины пластины X.
Согласно постановке задачи, предыдущие аргументы справедливы как для охлаждения пластины в более холодной среде, так и для нагрева в более теплой среде. Начальная температура 0°в обоих случаях представляет собой разницу между равномерной температурой тела (при / == 0) и окружающей средой. temperature. At температура внутри пластины 0, температура окружающей среды получается как нулевая точка (то есть значение температуры пластины, / — > oo).Тоже фигура. На рис. 20а и в показаны оба этих процесса. И значение 0°, потому что направление 3 касательных известно, вы можете создать кривую распределения температуры в плите с достаточным precision.
Факт, от консенсуса, потому что с другой стороны он очень хорошо отделен(a = 0).в этом случае направляющие точки, соответствующие этой стороне, удаляются бесконечно. Это означает, что температурная кривая имеет горизонтальную касательную на протяжении всего процесса охлаждения. Таким образом, все уравнения и кривые распределения б Тоже фигура. 20.Принципиальная схема выравнивания температуры в плоской пластине с однородным начальным температурным полем и конечным коэффициентом теплопередачи. а-охлаждение, б-нагрев. Но… Как и в основной задаче, если X — это не только общая толщина пластины, но и не половина толщины, то температура в этом случае все еще действительна.
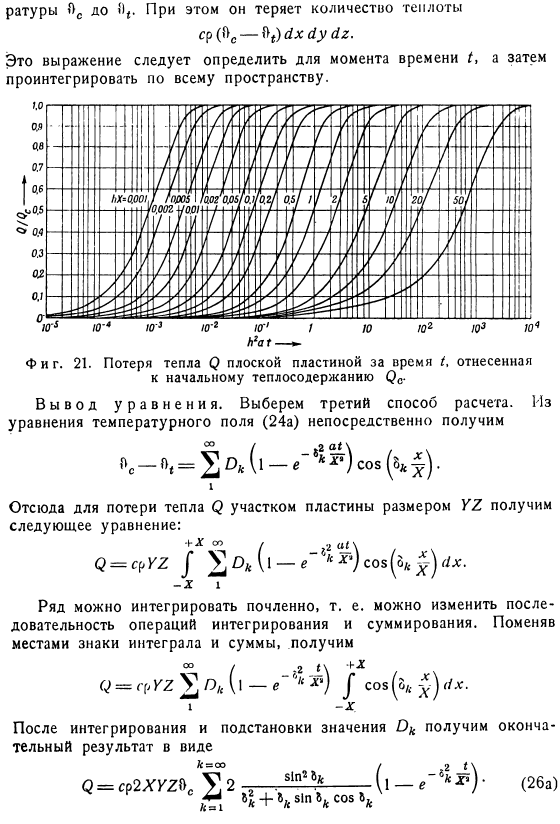
Определение тепловых потерь(?。3 методы расчета. Первый способ calculation. In тем временем на поверхностные элементы пены из внутренних слоев корпуса (11) поступает следующее количество тепла: Как рассчитать общее количество тепла(?Данная из тела формула должна быть интегрирована на обеих поверхностях с интервалом времени от 0 до/.* 2-й метод расчета. Поверхностные элементы (период 61, 1у1х、 Эта формула должна быть интегрирована на обеих поверхностях. 3-й метод расчета. Основной объем пластины bhbub с течением времени от 0 до I охлаждается температурой.
В этой формуле первым фактором, то есть cp2XI70s, является начальное количество тепла в организме, которое определяется по отношению к температуре окружающей среды. C) C, чтобы показать это. Остаток выражения (бесконечная сумма) является чисто числовым фактором, всегда меньше 1.Этот элемент определяет ту часть начального тепла пластины, которая будет потеряна в течение времени I. It является функцией (AX) с одной стороны, и ACX2 с другой. Эти переменные были сделаны выше.
Смотрите также:
| О согласовании с условиями на поверхности | Температурное поле стремится к равновесию. Цилиндр |
| О согласовании с начальными условиями | Температурное поле стремится к равновесию. Шар |

