Оглавление:







Теплообмен при турбулентном движении. Входные эффекты
- Рай находится в турбулентном состоянии внутри трубы. Это, пожалуй, самый распространенный случай теплопередачи в промышленности. Принудительная конвекция может сочетаться с ламинарными и турбулентными течениями со свободной конвекцией, но эти случаи имеют второстепенное значение. Коэффициент теплопередачи турбулентного движения выше, чем коэффициент теплопередачи ламинарного движения, и теплопередающее оборудование обычно рассчитывают, чтобы воспользоваться этой ситуацией.
| Теплообмен при развивающемся профиле скорости | Аналогия между переносом импульса и тепла |
| Теплообмен при развитом профиле скорости в трубе | Применение анализа размерностей к теплообмену |
Состояние знаний о теплопередаче в турбулентности неизбежно ограничено степенью знаний об изотермической турбулентной утечке. Ч.13 что использование уравнения Навье-Стокса при исследовании изотермической турбулентности затруднено пульсацией составляющих скорости. По этой же причине было установлено, что трудно использовать дифференциальное уравнение энергии при исследовании неизотермических turbulence. In большая часть турбулентности, тепло в основном передается за счет движения ряда макроскопических жидких элементов (вихрей) между различными температурными областями.
Величина коэффициентов теплопроводности газов на порядок меньше теплопроводности жидкостей. Людмила Фирмаль
Поведение этих вихрей невозможно предсказать, но, если это возможно, уравнения, описывающие это поведение, вероятно, будут очень сложными, поэтому одновременные решения уравнения движения и уравнения энергии будут невозможны. Тем не менее, вам нужно найти решение этих проблем problems. In в этой главе мы рассмотрим некоторые теоретические результаты, используемые в технологии, а в следующей главе рассмотрим расчетные соотношения. Пределы их значения и применимости помогают установить заявленную теорию.
В предыдущих главах мы рассматривали теплообмен в ламинарном потоке, а в первой части рассматривали теплообмен в развивающемся потоке, а затем в развитом потоке. Входной эффект, связанный с развитием потока, также присутствует в турбулентном потоке, что может значительно повлиять на общую эффективность теплообмена в потоке за короткое время. pipe. As как только он проходит через входной участок, коэффициент Коэффициент теплопередачи в развитом турбулентном потоке остается практически неизменным constant. It оказывается, это не относится к ламинарному течению. Входной эффект pipe. At на входе существует множество возможных сочетаний тепловых и гидродинамических условий.
В следующем примере предполагается, что жидкость поступает в трубу при равномерно распределенной температуре и что стенка трубы находится при постоянной температуре, превышающей температуру поступающей жидкости. Учитываются некоторые условия входного потока, и на основе полученных до настоящего времени данных гидродинамики и теплообмена качественно устанавливаются их влияние и локальный коэффициент теплопередачи. 1 жидкость поступает в трубу с равномерным распределением скорости*со скоростью, например, Be 2100.В этих условиях развивается ламинарный пограничный слой, начинающийся от передней кромки, пока он не встретится со всей трубой на определенном расстоянии от передней кромки. inlet.
Входной, коэффициент теплопередачи равен бесконечности. После достижения разработанного курса продолжится снижение. Этот случай рассматривался в предыдущей главе. 2. Жидкость поступает в трубу в ламинарном потоке с равномерным распределением скорости и расходом, таким как He> 2100.Это условие может быть выполнено с круглым входом. На границе образуется ламинарный пограничный слой. inlet. It становится турбулентным на критическом расстоянии, как описано ранее в разделе 2.12 для обтекания плоской пластины. Толщина турбулентного пограничного слоя увеличивается с увеличением расстояния от входа, пока он не заполнит всю трубу и не образует ламинарный подслой с турбулентным ядром на входе.
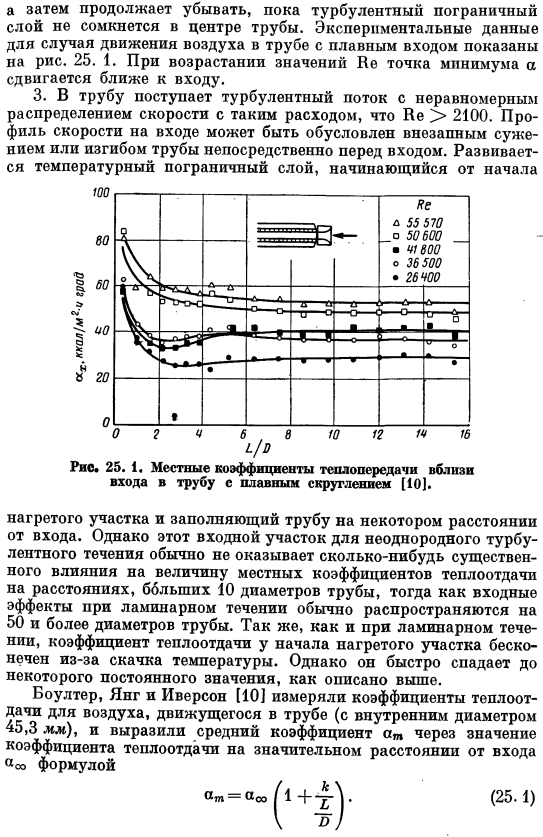
Кроме того, во всех отношениях поток идентичен потоку, развиваемому при турбулентном входном потоке. Характер этого течения отражается в значениях локальных коэффициентов теплопередачи. Локальный коэффициент теплопередачи уменьшается от бесконечности входного отверстия до некоторого минимума критической точки, в которой ламинарный пограничный слой заменяется турбулентным слоем. Вблизи этой точки коэффициент теплопередачи увеличивается на коротком участке, а затем продолжает уменьшаться до тех пор, пока турбулентный пограничный слой не закроется в центре трубы. Экспериментальные данные в случае движения воздуха в трубе с плавным входом показаны на рисунке. 25. 1.
При увеличении значения Be минимальная точка сдвига приближается к входу. 3. Турбулентность с неравномерным распределением скорости потока, например Be> 2100, профиль скорости на входе в трубу может быть обусловлен резким сужением или изгибом трубы непосредственно перед входом в трубу. inlet. It начинается с пэчворка и развивается пографический слой температуры Я К И затем — ■> ■■ * Не l 55570 около 50 600■41800 около 36500 * 26400 д’ 11°■ — м. 1 ″ б » — » е■ ■ ■ 1 * O 2 4 6 8 10 1%14 16 Рисунок 25. 1.Локальный коэффициент теплопередачи (10) вблизи входа в гладкую округлую трубу. Заполните трубу на некотором расстоянии от нагретой части и входа.
Однако этот входной участок неоднородной турбулентности обычно не оказывает существенного влияния на величину локального коэффициента теплопередачи на расстоянии более 10 диаметров трубы, тогда как входной эффект в ламинарном потоке обычно распространяется на более чем 50 труб diameters. As в ламинарном потоке коэффициент теплопередачи в начале нагреваемого участка становится бесконечным из-за повышения температуры. Однако, как упоминалось выше, он быстро падает до определенного постоянного значения.
Бултер, Янг и Иверсон [10]измерили коэффициент теплопередачи воздуха, движущегося по трубе (внутренний диаметр 4°, 3 ЛМС), и выразили средний коэффициент по значению коэффициента теплопередачи в месте, которое довольно далеко от входа из уравнения. «Т -» ОО (1) (25.1) значение k зависит от входных условий, как показано в таблице. 25.1.At на расстоянии менее 5 диаметров от входа формула имеет вид Это уместно. Таблица 25.1 Значение k в Формуле (25.1) Тип ввода………………….. Плавное скругление……………… 1.

- Гладкая закругленная одной решеткой короткая седативная секция на входе с острыми краями(G / R = 2,8). Длинный успокаивающий участок с острыми краями на входе(G / R = 11,2)……………………… Входите под углом 45°…………… Вход на 90°…………… Диафрагма с цилиндрическим отверстием диаметром 254«на расстоянии 5 мм от входного отверстия. 。 …. Диафрагма с цилиндрическим отверстием диаметром 254 мм на расстоянии 254 мм от входного отверстия Эксперимент на входе с диафрагмой (и для простого входа с острым краем) показал, что на графике зависимости а имеется максимальное значение между 1 и 3. Турбулентность вдоль плоскости plate.
В предыдущей главе мы рассмотрели коэффициент теплопередачи в области ламинарного пограничного слоя на плоской пластине, основываясь на основном дифференциальном уравнении. Эта задача также может быть решена полуэмпирическими методами с использованием так называемого метода интегральных соотношений кармана. Эта глава учитывает турбулентность и использует метод интегральных соотношений для получения приближенного решения задачи, поскольку уравнение Навье-Стокса не может быть использовано.
Как видно из таблиц, среди твердых тел металлы обладают наилучшей теплопроводностью. Людмила Фирмаль
Применение метода интегрирования к изотермическому потоку уже было показано в разделе 2. 13.Мы записали приближенную формулу для распределения скорости пограничного слоя и применили уравнение баланса импульса к элементам этого слоя. Таким образом, получена формула для коэффициента сопротивления поверхности пластины.
Форма уравнения распределения скоростей (13.95) имеет вид «Х-( ’на’ 1 ′ ^ 〜 \ б)• В этой задаче мы предполагаем, что распределение температуры описывается аналогичной формулой (25.2) Поскольку число Прандтля предполагается равным 1, то оно будет равно b = d/, что является границей контрольного объема на рис.3. 25. 2-граница гидродинамического пограничного слоя и температурного пограничного слоя одновременно. игнорируйте вязкую диссипацию и теплопроводность в направлениях x и r. Рисунок 25. 2.Контролируемый объем для исследования теплообмена в турбулентном пограничном слое.
Тепло поступает в систему с потоком жидкости через плоскости 4X и 43 и выходит из системы с потоком жидкости через плоскости A2.It также возникает в результате теплопроводности через часть пластины в области L4. Формула энергетического баланса управляющего объема приведена на рисунке (4. 6) пишите. 25. 2. игнорировать ЧР изменения»* Кинетическая энергия-y и потенциальная энергия#2. Энтальпия I выражается произведением CP1.Движение неподвижно, поэтому нет внешнего при= 0 Работает, IV,=0.Теплопроводность через участок L4 позволяет теплу поступать в контролируемый объем、 5 = Ф / топор (^- «0) Один * Уравнение энергетического баланса принимает вид / 1 csr *и cos + G T dSr! И cos д.
А + $ CP1 и потому, что с М = А » А » А » А » Один (25.3) Поверхность А! И, cos a = — ih, а поверхность A2 и cos a =к ним、 ΓСC ^ x ^ + / » » x + H & p1 и co3 и aA = А, Ля А、 =Λ » x (^- У^.(25.4) Один * Для дальнейшего упрощения мы связываем массовый поток через прокладки A»A2 и A3 со следующими соотношениями, полученными для несжимаемых жидкостей: 13 [опорное выражение.
Поскольку температура жидкости на верхней границе пограничного слоя (участок А3) постоянна и равна температуре свободного течения 20, (13.Если умножить 81) на 10 и подставить полученную формулу уравнения (25.4) вместо Интеграла А3、 И(A> (- Y » x (A (I-10)) их d, A = Да. = «„Х?“- Г ^ (255) Один Поскольку ширина всех колодок одинакова, а значения не изменяются в направлении оси z, двойной Интеграл уравнения (25.5) может быть заменен одним интегралом с соответствующим интегральным пределом. б, б, х、 / / ЗТП(1 ^ 1о) их^ г ^ / топор (б * 0м *.
Предполагая здесь, что длина x2-стремится к нулю, левая часть уравнения (25.6) становится производной, а правая-тепловым потоком от конечной ширины и бесконечно малой длины платформы. Поэтому мы имеем L / hCr(1 — {0) ihs1y = топор (Отсюда (25.8) Безразмерная температура под знаком интеграла、 * ~ ~ * 0 -. Четыре ^ 8-1о Это еще не все. ^ 8 ^ 0 (25. Девять) ІА = ц0 (25.10) Ф(25. 8) Формула (25. 9) и (25. 10) замените интегральную переменную y, замените верхнюю границу интеграла. топор = eCri0 (25.111) Этот Интеграл может быть вычислен непосредственно. Его численные значения равны, поэтому локальный коэффициент теплопередачи равен Р 7 ад » х-е ^ ОТГ -^- Ch.
Найденная на рисунке 13 толщина границы представляет собой отношение(13. 102). 4 = 0,376 (веха) (25.12) Слой D Если продифференцировать это уравнение、 1/’.Ах ’ т = = о, zo1 все Ке ^. ^ = 0.376(-7 классы’ — ал \ УО / Если мы подставим эту формулу для дифференцирования(25.12)、 (25.13) В Формула ^ = 0 ′ 0292Kech -«. (25.14) Если вы умножите обе стороны этого уравнения на u, Далее, мы получаем выражение для локального числа нуссельта. Ми «= 0.0292 Быть * » РГ. Pr = 1, поэтому конечная форма этого выражения является Литий= 0.0292 Бэу’.
Если уравнение ah должно быть интегрировано от передней кромки пластины до расстояния x, как это было сделано в разделе 24, чтобы получить среднее число нуссельта ] Yait = 0,0365 Быть ’/ *. (25.16)) Этот вывод уравнения Миеса основан на предположении, что турбулентный пограничный слой начинается на передней кромке. Однако турбулентный пограничный слой начинается при критическом значении Кех>, которое приблизительно равно 500 000, и ему предшествует ламинарный пограничный слой.
Локальный коэффициент от передней кромки до критического расстояния определяется по формуле (24.8) и превышает критическую точку по формуле(25.15).С этой формулой, вы, ЭМ, всегда должны брать расстояние от передней кромки пластины, а не от места турбулентности. Если большая часть пластин покрыта ламинарным пограничным слоем, то прямое применение формулы (25.16) является ошибочным. Вместо этого формула от x = 0 до конца ламинарного сечения(24. 8) и формулу от этой точки до конца пластины 25.
Смотрите также:

