Оглавление:








Теплообмен при развивающемся профиле скорости
- Ламинарное течение вдоль плоской пластины. Задача о передаче тепла жидкости, которая движется параллельно пластинкам к плоской пластине, была решена Полхаузеном. Его решение основано на дифференциальных уравнениях непрерывности энергии и импульса, которые были выведены ранее(Глава 9-я).Применение уравнений непрерывности и импульса к задаче определения поля скоростей изотермического ламинарного течения вокруг плоской пластины описано в разделе.
Расширьте это рассмотрение и примите во внимание передачу тепла от пластины к жидкости, дифференциальное уравнение энергии(10. I) писать. Д1. Д1. Д1. Д1 х /нет, Dн, Dн \ Если поток 2-D, то u =0.Стационарный case=0.In кроме того, игнорируют теплопроводность всех направлений, кроме направления, перпендикулярного пластине, dF _ A dx ^ В результате получаем уравнение Д1 Д1 х + ОС’ (24.1) это уравнение является импульсом песни Аналогично ранее упрощенным уравнениям дичь,»Дич вопрос d2ih у ^〜ДГ + и» из-за ’9ug’ (24. 2) с уравнением неразрывности (24.2) Из уравнения (12. 44) получено распределение скоростей ламинарной границы layer.
В настоящем параграфе мы займемся определением теплового потока для простейшего случая, а именно для стационарного режима и плоской стенки, и вместе с этим выведем основные законы теплообмена. Людмила Фирмаль
Здесь безразмерная скорость выражается как функция величины* /(представленная q). Если количество Прандтля в жидкости равно 1、 Икс Насколько легко проверить теплопроводность и кинематику Вязкость составляет equal. In кроме того, уравнение(24. 1)когда температура заменена безразмерным параметром Уравнение (24. 1) и (24. 2) граничные условия одинаковы. Рассмотрим только, если пластина находится при постоянной температуре I. Для удобства предположим, что 1L больше температуры жидкости на границе температурного пограничного слоя 10. если y = 0°, ТО^-= 0; * 0 ″ 0 Если Y = oo I = 0 4 r8 — * o — = 1; » 0 −1, — 2в = 1.
Дифференциальные уравнения энергии и импульса(24. 1) и (24. 2) видно, что он совпадает с приложенным к жидкости числом Прандтля, равным 1.So у них одно и то же решение. То есть в любой точке потока (g, y) размерно скорость-и температура равны. Решение для этого Профиль скорости показан на рисунке. 12.8 одинаково хорошо подходит для температурного профиля determination. So в этом случае существует прямое соответствие между процессами теплопередачи и передачи импульса, а толщина температурного и гидродинамического слоев равна.
Эти результаты важны, потому что многие газы и жидкости, такие как вода при 190°C, имеют близкое к 1 число Прандтля. Однако в общем случае число Прандтля жидкостей находится в диапазоне от 0,001 до 1000, а в некоторых случаях оно выходит за пределы этого диапазона. Полхаузен расширил раствор до жидкости с другим числом Прандтля, чем унифицированное one. An обзор его методов приведен ниже. Ч. Используйте тот, который введен в 12 переменных-отношение (12. 68),(12.69),(12.72) и 12.
Безразмерная температура (b —)/ (»- A>)«производное уравнение энергии(24. 1)следующее уравнение будет: Д2 Л’ Пр /(п)\ * С / О / Два = 0、 (24.3) Это может быть непосредственно интегрировано методом, используемым для решения обыкновенных дифференциальных уравнений. Подробности этого указа приведены в книге Кнудсена и Каца[851.Зависимость, определенная для изотермического течения/(μ), имеет вид ранее приведенного ряда-формулы(12. 74).Порхаузен использовал эту зависимость для получения температурного профиля жидкости в широком диапазоне чисел Прандтля. Некоторые из этих профилей показаны на рисунке. 24.
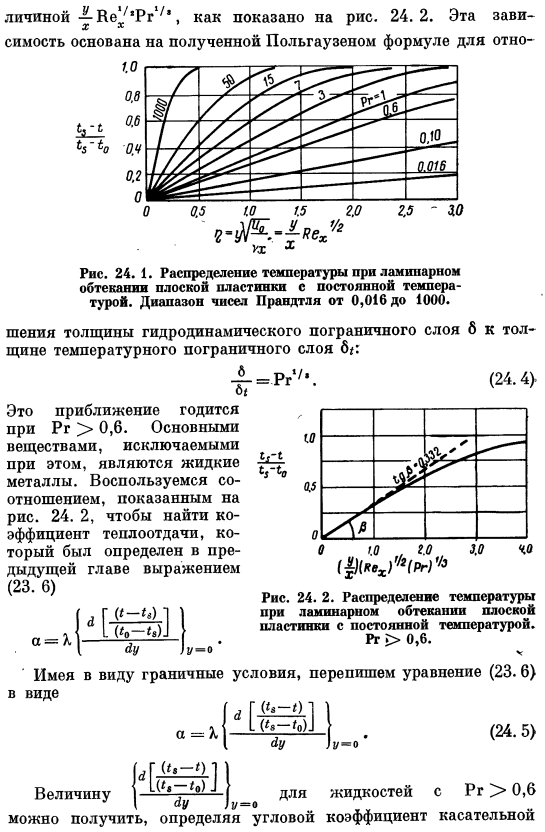
Значение q используется на рисунке 24. 1 также можно записать как −1/.Здесь можно выделить 2 безразмерные группы Х г в Пи-и тогда. Последнее значение является локальным числом райполя, обычно обозначаемым Вех (индекс указывает расстояние X от передней кромки пластины). Решение показано на рисунке 24. 1, соответствующий для широкого диапазона числа Прандтля жидкостей. Для узкого диапазона Pr> 0,6 жидкости эмпирически установлена кривая 24. 1 может быть представлено одним соединением, соединяющим безразмерную температуру. — «0» Маска Be ^Рг1 ^ как показано. 24.2.Это зависит О 0.5 1.0 1.5 2.0 2.5-3.0 Рис.
Распределение температуры в ламинарном потоке вокруг плоской пластины при постоянной температуре. Диапазон числа Прандтля составляет 0,016-1000. От толщины гидродинамического пограничного слоя 6 до толщины температурного пограничного слоя 6: А = пр * /.(24.4). О / Это приближение подходит для PR> 0.6.Основным веществом, которое исключается в этом случае, является жидкий металл. Используйте связи, показанные на рисунке. 24. 2, формула в предыдущей главе 23.
Распределение температуры в ламинарном потоке вокруг плоской пластины при постоянной температуре. РГ> 0.6. Обратите внимание на граничное условие и перепишите уравнение (23.6 В форме ГСЕТ| ]> Один) г = о (24. Пять) ИГ и-около 1 Pr> 0,6 жидкостный случай Размер Она получается путем определения углового коэффициента касательной кривой на рисунке. 24. 2 и y He ^ Tr * 7 * =0.Этот угловой коэффициент равен 0,332. Таким образом, коэффициент теплопередачи ah может быть выражен следующей формулой: AJ = o; s ^ 2He ./. pr -/.
Безразмерная группа является важной величиной、 Он известен своей теплопередачей, называемой числом нуссельта. Где X-характерная длина. В зависимости от координат, если число нуссельта содержит коэффициент теплопередачи ax, то число нуссельта также зависит от координат и указывается ими. Следовательно, формула(24. 7) очевидно, что его можно прекрасно описать в безразмерных величинах. Н11 * = 0.332 Ной * РГ международный. (24.8) Формула 24.
- Определить локальный коэффициент теплопередачи ax на расстоянии x от переднего конца пластины. Если мы найдем средний эффективный коэффициент теплопередачи для всего участка от передней кромки до точки x, то получим его следующим образом: д = Од («а -» о)= / топор (*, — * о) ух Б,(24. Девять) О Где b-ширина пластины в направлении оси 2.Температура пластин постоянна, поэтому разница составляет 10 констант. И затем… на.±= =(24.10) О, да. Таким образом, средний коэффициент теплопередачи в выражается формулой: a _ 0.332 u0 y / «(Срру / » (ёдч*) = 0.664 ^ ^ рну7\ (24.11) Это выражение можно записать в безразмерных величинах: Горит= 0.664 Ее / — Пр1/’.
Обозначение вех используется в уравнениях, которые содержат локальные коэффициенты. Символ Be ^используется в уравнениях, содержащих средние коэффициенты, связанные с участком поверхности длины B. Показано, что пограничный слой с ламинарным потоком 12 сохраняется на гладкой пластине до тех пор, пока число Рейнольдса не будет приблизительно равно 5×10b. очевидно, что исследование теплообмена, проведенное в этой главе, имеет то же самое limitations. In кроме того, не забывайте, что формула (24.6)-(24.12) применима только к Pr> 0.6. Пример 24. Один Воздух с постоянной скоростью 15 м при температуре 22°С движется параллельно плоской пластине, которая нагревается до 100°С.
Затем тепло должно пройти через стенку и, наконец, оно воспринимается с противоположной поверхности стенки более холодным газом (или более холодной жидкостью). Людмила Фирмаль
Теплопередача на критическом расстоянии и средний коэффициент теплопередачи части пластины покрыты ламинарным пограничным слоем. Воздух при температуре 66°C имеет следующие параметры: В = 0.2 * 10 «* мч; К = 0,0244 ккал / м * ч * град; РГ = 0.72. Если число Рейнольдса установлено на критическое значение 5 * 10е, то определяется длина ламинарного пограничного слоя. когда вы решаете x, это выглядит так: at_ 5■108 » 0.2 ″ 10- * Пятнадцать Толщина гидродинамического пограничного слоя определяется по формуле (12. 75). _ П 6 = 5,0 1/. Г ц0 при x = 0,67 м найдите следующее: * з /0.2-КН-0.67 \ х / » b-5(———-} = 0.0048 м. Толщина температурного пограничного слоя равна x = 0,67 by.
Формула (24.4): 0.0048 _ 0.72 * 0.0048 0.895 = 0,0054 м локальный коэффициент теплопередачи при Х-0,67 рассчитывается по формуле (24. 7) определяется по: = deCh1rg 1 /. =(5.линия U6)1 /.* ккал / вт2 * Йорай. Средний эффективный коэффициент теплопередачи участка пластины от передней кромки до точки, где ламинарный пограничный слой является турбулентным (x = 0.67 л), равен локальному коэффициенту при x = 0.67 (2x). таким образом, при = 2ax = 15.4 ккал / м * * ч * град. Теплопередающая жидкость к жидкости, поступающей в T P V b V, обычно поступает в трубу с равномерным распределением скорости и температуры.
Когда стенки трубы охлаждаются или нагреваются по всей ее длине, на входе в трубу начинают формироваться как гидродинамический профиль скорости, так и температурный профиль. pipe. As в случае обтекания плоской пластины локальный коэффициент теплопередачи имеет бесконечное значение на входе и уменьшается в удаленной части трубы до определенного предела. Задача развития гидродинамического пограничного слоя решается изотермическим потоком, и уже Ч.
Проблема одновременного развития гидродинамических и температурных слоев была исследована в случае 1811 года. Его подход состоял в использовании результатов Лангхаара, связанных с развитием профилей скорости в численном интегрировании дифференциальных уравнений энергии. Он получил раствор с постоянной температурой стенки, равномерным тепловым потоком от стенки и ограничением на жидкость Pr = 0,7 при определенных условиях разности температур между стенкой и жидкостью. Естественная конвекция вблизи вертикали walls. An важным случаем в этой технике является передача тепла от вертикальной стенки к жидкости, движущейся параллельно стенке за счет естественной конвекции.
Естественная конвекция возникает в системе, в которой плотность жидкости изменяется в пространстве. Однако, если жидкость вынуждена двигаться, эффекты естественной конвекции обычно незначительны. Когда поток уменьшается из-за принудительной конвекции, оба механизма показывают области важности. Примеры, описанные в этом разделе, являются ограничительными случаями, когда упражнение вызвано только нагреванием. Эта задача может быть решена с помощью уравнений непрерывности и энергии, показанных ранее при рассмотрении вынужденного ламинарного течения вокруг нагретой пластины.
Однако энергия массы должна быть введена в дифференциальное уравнение энергии с учетом влияния силы тяжести на нагревание liquid. As в результате уравнение импульса описывается следующим образом: е (топор (- м +и•(24.13) Массовые силы, вызванные изменением плотности, важны в этом уравнении, но поскольку влияние сжимаемости на другие члены дифференциального уравнения незначительно, эти уравнения могут быть использованы с учетом констант параметров жидкости. Эта система уравнений была решена*для отопления Решение Польгаузена, например、 [74].Идеальный двухатомный газ за счет естественной конвекции при постоянной температуре вертикальной стенки.
Это решение, записанное в безразмерных величинах、 Гнида = 0.478 КЛ * 7 *、 (24.14) Где среднее число нуссельта IIT = amKI \ Grashof число Cr == Коэффициент теплопередачи — это средний коэффициент площади от нижнего конца ступени до точки, расположенной на расстоянии b от нижнего конца. Этот коэффициент используется в температурной головке, которая равна разнице между температурой стенки и температурой вне температурного пограничного слоя.1Т или 10.Температура в знаменателе числа Грашофа обратно пропорциональна коэффициенту объемного расширения p. это только идеал gas. In вообще, грашоф граф включен в большинство зависимостей естественной конвекции. Формула (24.
Подходит только для полного ламинарного потока. Турбулентность рассматривается в секундах. 25 и 26. Остальные случаи. Другие случаи передачи тепла в ламинарном потоке, где разрабатывается профиль скорости, представляют интерес для инженеров.1. одним из случаев является такая плоская пластина, нагревательная часть которой начинается на определенном расстоянии от ведущей edge. In кроме того, когда температурный пограничный слой начинает развиваться, гидродинамический пограничный слой уже частично развит. Существенное значение имеет проблема бокового обтекания нагретого цилиндра и обтекания сферы.
Если число Рейнольдса мало, если существует ламинарное течение без отрыва, то можно получить численное решение дифференциальных уравнений. Однако в наиболее важных случаях на практике поток отрывается от поверхности цилиндра и требует применения эмпирических методов. По этому вопросу вы можете обратиться к статье Onch.
Смотрите также:
| Коэффициенты загрязненности | Теплообмен при развитом профиле скорости в трубе |
| Теплообмен при ламинарном движении | Теплообмен при турбулентном движении. Входные эффекты |

