Оглавление:







Теплообмен при наличии химического источника тепла
- Химические реакции обычно проводят в проточном реакторе с неподвижным слоем катализатора. Схематично конструкция такого реактора показана на схеме. 9-5. Реактор занимает пространство длиной от z = — ⁰ ⁰ до z = + °o, содержащее 3 зоны. Реакционная зона заполнена соплом, выполненным из частиц катализатора. Входные и выходные зоны также заполнены соплами. Однако его частицы не обладают каталитическими свойствами, и их физические свойства сходны только с частицами катализатора в реакционной зоне. В описании химического реактора часто используется так называемая поршневая модель течения. Это означает, что градиент радиальной скорости равен ignored.
Кроме того, предполагается, что температура практически не зависит от радиальных координат R. Это предположение оправдано для реакторов с изолированными стенками. Задача состоит в том, чтобы найти устойчивое распределение температуры T (z) при условии, что при попадании жидкости или газа в реактор(z = −00).Постоянная температура по сечению 7 \и убывающая скорость= w (nr’PJ) −1(см. раздел 6-4). Аналогичная задача может быть решена в предположении, что теплообмен в направлении оси z описывается законом Фурье теплопроводности с» эффективной теплопроводностью » упакованного материала bed.
Тепловой поток на поверхности, ограничивающей высокоскоростной поток, может быть вычислен по формуле, которая является справедливой для низких скоростей, когда разность температур, определяющая поток тепла, введена надлежащим образом, а именно как разность между температурой восстановления поверхности и ее действительной температурой. Людмила Фирмаль
В литературе имеется множество экспериментальных исследований по измерению эффективной теплопроводности упакованного слоя осевого (XeF) радиального (k, ef) направления. Эти величины играют важную роль в теории каталитического реактора и, как показывают экспериментальные данные, численно существенно отличаются друг от друга. Когда во время химической реакции атомы реагирующих молекул перестраиваются и образуют конечный продукт、 Высвобождение или поглощение тепловой энергии. Объемная скорость выделения тепловой энергии в результате химической реакции показана в СК, но, как правило, это очень сложная функция давления, температуры, химического состава и каталитической активности.
Для простоты предположим, что СК определяется только температурой, причем еще более линейно. SC = SC (9.75) ) В этом уравнении T обозначает локальную температуру слоя катализатора(при условии, что поток частицы катализатора и жидкость или газ, обтекающие его, имеют одинаковую температуру*). Значения Sc 1 и T°являются константами опыта, которые определяются условиями на входе в устройство. Расчет •Однако следует отметить, что различия между свежими средами и частицами катализатора, такими как задачи 20-8 и 20-9, незначительны. Вы можете запустить реактор, используя более реалистичное выражение в Sc, но вы должны использовать числовой метод.
Чтобы сбалансировать тепловую энергию, выберите диск с радиусом R и толщиной Da в зоне реакции(см. рис.9-5) и толщиной Az так, чтобы он был намного больше размера частиц катализатора.
В предположении, что установившийся энергетический баланс включает следующие элементы: Процент тепловой энергии, поступающей на выбранный диск через секцию z ЯЯ ’ яг1г (9.76) Отвод тепловой энергии от диска по теплопроводности через поперечное сечение z + (9.77)) Скорость теплоты через поперечное сечение z в результате потока жидкости или конвективного переноса энергии с помощью Rasa py2r1N1Sr(G-2’₀)|, (9.78) Скорость конвективного отвода тепловой энергии диска через сечение z +Дг nflSppidp (Г — Д)|Г₊ДГ(9.79) Уровень тепловыделения 。(lL2dg) г«(9.80)) Где удельная теплоемкость Cp принимается постоянной для данной реакционной смеси, массовый расход nR’pyfi выражается в плотности и скорости на входе в реактор.
Заметим, что тепловая энергия движущейся сплошной среды регистрируется относительно определенной фиксированной температуры T o в качестве точки отсчета температуры. Введение такой точки отсчета необходимо, так как количество энергии не может быть выражено в абсолютных единицах. Затем подставьте формулу (9.76)-(9.80) в общее уравнение теплового равновесия (9.1) и разделите все его члены на nR2Az.
- Тогда вы получите, передайте выражение (9.81) в предел как г-> 0. Тем не менее следует иметь в виду, что, пройдя такой предел до крайности, конечное уравнение будет усреднено, а не точечно, поскольку среда, в которой описывается формула (9.81), не является полностью непрерывной (в этой среде имеются дискретные твердые частицы). Над поперечным сечением реактора q₂, T и Sc. Указанный переход ограничения дает следующее выражение: -^-+ Р1> ГПУ-^-= 5е. (9.82) В уравнении (9.82)содержимое реактора рассматривается как сплошная среда, и подставляется формула для Правила Фурье теплопроводности.
Если предположить, что эффективная теплопроводность в осевом направлении, равном X2Eff, постоянна, то подставим правило Фурье в Формулу (9.82), а затем получим уравнение распределения температуры. (9.83) Если значение Sc для этих зон равно нулю, то формула (9.83) справедлива также для зон I и III. Поэтому распределение температуры в реакторе, показанное на фиг. 9-5, описывается следующей системой дифференциальных уравнений.
Вычисление постоянных в уравнении (10-1) из этих граничных условий дает: Тепловой поток к поверхности 0 находим из выражения 2с Это выражение может быть упрощено путем введения температуры восстановления. Людмила Фирмаль
Ион I (z Вода пихи AT1di (9.84) (9.85) (9.86). Эффективная теплопроводность (A и Ef) всех 3 зон считается одинаковой. Система 2-го дифференциального уравнения(9.84)-(9.86) должна быть решена при следующих 6 граничных условиях: для z = — oo, для Γ =₁₁s = 0, tr = Tn «ст1, ДТУ в» = 0 = ^ ’ ф-5г z = L в ТЧ ₌ ТП1 _. 。 почтовый индекс dt11. МТП prpg-л- (9.87) (9.88) (9.89)) (9-90 )) (9.91) (9.92) Условия (9.88) — (9.91) представляют непрерывность температуры и теплового потока на границе раздела соответствующих областей. Дополнительные условия(9.92) основаны на простых физических соображениях. d решение сформулированной выше задачи значительно облегчается введением безразмерных переменных.
Решение системы линейных однородных дифференциальных уравнений (9.97) — (9.99) представляет собой комбинацию следующих 3 функций: Куда? 0F = Ci +Cebebz Е,,, = С, ЭМ, з +C₄e «Укрзализныци forт₃ ^ = пц 0 » I =C₆+Cebebz (9.103) (9.104) От граничного условия (9.92) до C,= 0.So, температура в зоне III постоянна во всех отношениях.
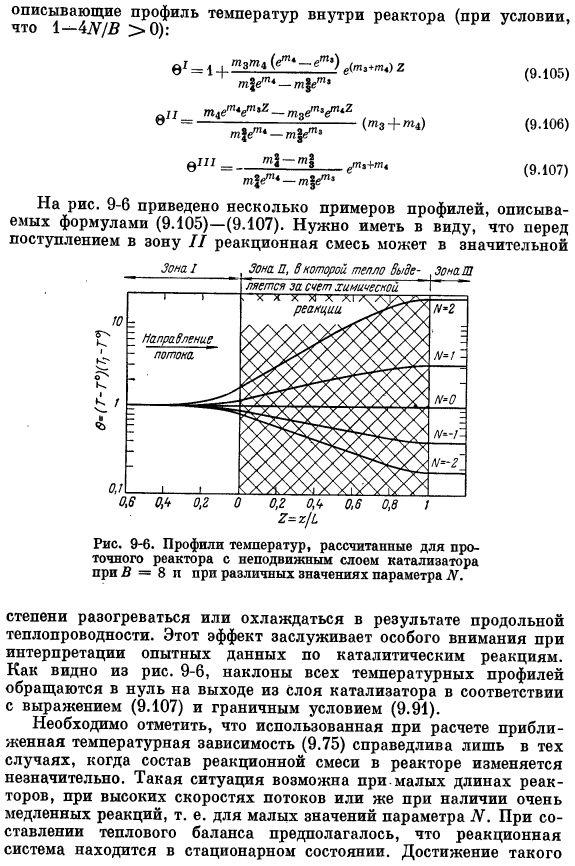
Для того чтобы граничное условие (9.87) было выполнено, соответствующий Ct должен быть установлен равным 1.Любые оставшиеся константы можно найти из граничного условия (9.88)-(9.91).После простого вычисления получается окончательное выражение、 Опишите температурный профиль внутри реактора(1-4LG / V> 0 случай (9.105) «И мемем (9.106)) (9.107) Рис. 9-6 показано несколько примеров профилей, которые иллюстрируют следующие Формула (9.105)-(9.107). ее необходимо запомнить до При входе в зону II реакционная смесь значительно уменьшается е(М. Н. З Степень нагрева или охлаждения в результате продольной теплопроводности.
Этот эффект заслуживает особого внимания при интерпретации экспериментальных данных по каталитической reactions. As как видно из рисунка 9-6, наклон всех температурных профилей исчезает на выходе из слоя катализатора в соответствии с формулой (9.107) и граничными условиями(9.91). Приближенная температурная зависимость (9.75), используемая в расчетах, справедлива только в том случае, если состав реакционной смеси в реакторе изменяется незначительно, и такая ситуация наблюдается при малой длине реактора, при высоком расходе или при медленной реакции, то есть при малом значении параметра N.
Если тепловой баланс совмещен, то предполагалось, что реакционная система находится в стационарном состоянии. Такое достижение Государство, вообще говоря, обеспечивается выбором соответствующих начальных условий. Физическая реализация стационарного режима теплообмена может быть установлена экспериментально или путем анализа нестационарных уравнений, соответствующих уравнению (9.97) — (9.99).Для систем, описанных в этом разделе, установившееся состояние не может быть установлено при очень высоком наконечнике ratios.
Смотрите также:

