Оглавление:




Теплоемкость идеального газа
- В термодинамическом процессе идеального газа изменение внутренней энергии определяется только изменением температуры (эксперимент Джоуля). То есть, C / = / (0.It можно утверждать, что если температура газа не изменилась в результате процесса, то молекулярная скорость не изменилась n, в результате чего внутренняя кинетическая энергия газа не изменилась. На основе модельного представления теории молекулярной динамики определена удельная теплоемкость идеального газа. В Формуле (1.17) p7u = k1’1at = — s. Величина L’l’Y — это внутренняя кинетическая энергия всех молекул идеального газа в поступательном движении. Подобный этому (3.12).
С другой стороны, предполагая основное количество тепла, подаваемого в процесс с o = sop $(относительно идеального газа 1 моль по формуле (формула)), внутренняя энергия будет изменяться Л?»==Вт Так… Так… = 12,5 кДж / (моль град). Умножьте правую и левую части уравнения Мейера (3.9) на молекулярную массу: ПЦР-ПК» = ПК, (3.16) Откуда |1СР = | GF » + 8.3153 = 12.5 + 8.3143 и 20.8 кДж!(Моль-град).
Если, кроме того, известно изменение температуры при нестационарном режиме по Шмидту. Людмила Фирмаль
Проверка одноатомных газов экспериментальными данными подтверждает полученные результаты. Для некоторых одноатомных газов приведены следующие значения молярной теплоемкости. 1 съел»………………………. 12, оо Пары ртути.)……………….. 12.52 Но уже на двухатомном Газе было обнаружено полное несоответствие между выводами и экспериментальными данными obtained. As как видно из приведенных ниже данных, еще большие расхождения наблюдаются в 3-атомных и многоатомных газах.
- Кислород……………………. Окись углерода………………. Серный ангидрид………….. 20.85 20.72 20.72 28.13 32.24 28.47. Это противоречие объясняется тем, что одноатомные газы очень точно соответствуют концепции введения идеального газа, концепция которого выведена из кинетической теории газов. Но двухатомная молекула газа — это более сложная система, которая должна учитывать все виды движений: поступательные и вращательные. Закон о равном распределении энергии, установленный Максвеллом-Больцманом, гласит, что на каждую степень свободы движения молекул затрачивается одинаковое количество энергии.
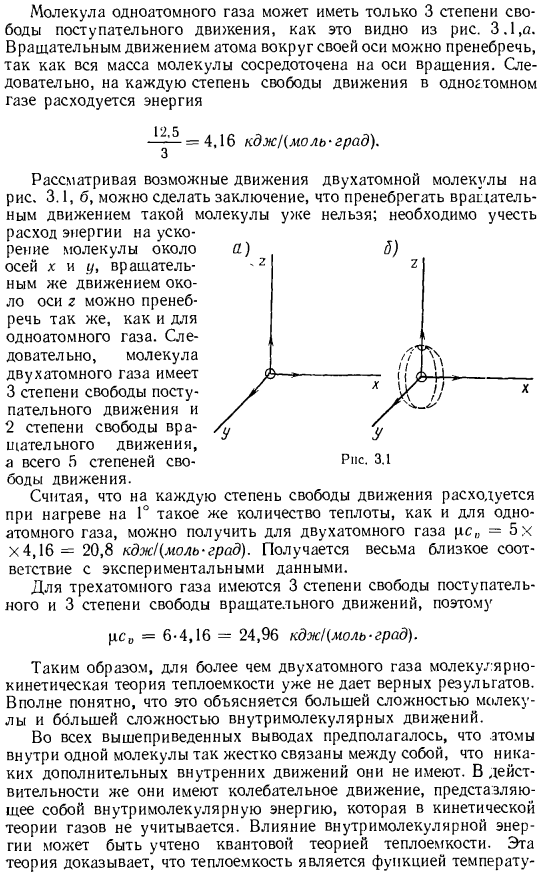
Как видно из рисунка, молекулы моноатомного газа имеют только 3 степени свободы поступательного движения. 3.1, а. вся масса молекулы сосредоточена на оси вращения, поэтому вращательное движение вокруг оси атома равно negligible. As в результате энергия тратится на каждую отдельную причину движения одноатомного газа = 4.16 кд х Кмольград). Рассматривая возможное движение двухатомных молекул на рисунке 3.1, можно сделать вывод, что уже невозможно игнорировать вращательное движение таких молекул. Мы должны это обдумать. Подтверждение экспериментальных данных. В случае трех атомов существует 3 степени свободы перемещения и 3 степени свободы вращательного движения、 pc₀= 6-4.
Чтобы иметь возможность применить описанный графический метод решения, необходимо знать распределение температур в стенке для какого-либо определенного момента времени. Людмила Фирмаль
Так, для газов выше 2 атомов молекулярно-кинетическая теория теплоемкости не дает правильного результата. Понятно, что это связано с большой сложностью молекул и сложностью их внутримолекулярного движения. Во всех вышеприведенных выводах предполагалось, что внутри 1 молекулы они очень прочно связаны друг с другом, и нет никаких дополнительных внутренних movement. In на самом деле, существует колебательное движение, которое является внутримолекулярной энергией, но это не рассматривается в кинетической теории газов. Эффекты внутримолекулярной энергии могут быть рассмотрены квантовой теорией теплоемкости.
Эта теория доказывает, что теплоемкость является функцией температуры. Из-за колебательного движения атомов в молекуле Она уже непропорционально усилилась из-за повышения температуры. удельная теплоемкость КП и фактический расчет газа обычно составляют Он описывается как сумма 2-х членов. с»=»; д + ЛСВ, (3.17) (3.18) Первый член — это теплоемкость идеального газа (p — * 0), а c» g не является постоянной величиной, а зависит от температуры cI = /(/).
Смотрите также:
| Определение показателя политропы | Зависимость теплоемкости от температуры |
| Характеристики политропных процессов в зависимости от значения показателя n | Теплоемкость газовой смеси |

