Оглавление:







Теория теплоемкости твердых тел (продолжение)
- Необходимо решить проблему естественной вибрации сплошного твердого тела, заключенного в жесткую стенку. Эта задача сводится к решению дифференциальных уравнений теории упругости при определенных граничных условиях. Это похоже на проблему электромагнитных колебаний в зеркальном ящике, рассмотренную в§ 20.Результатом решения является: В твердых телах это могут быть как продольные, так и поперечные колебания.
Каждое нормальное колебание является либо стоячей волной с продольным колебанием, либо стоячей волной с поперечным колебанием, направленным в определенном направлении. Частота этих колебаний выражается точно так же, как и частота электромагнитных волн(§ 20).Число поперечных колебаний в интервале (ω, w +¿c) выражается формулой (20.17). оно равно Где c-скорость поперечной упругой волны в Кристалле, а V-объем Кристалла. Правда, возможны 2 независимых нормальных колебания определенной частоты.
Закон Куба теплоемкости также экспериментально обоснован при низких температурах (£27). при высоких температурах сохраняется классическое представление средней энергии. Людмила Фирмаль
Поляризации отличаются друг от друга, каждая из которых имеет свою собственную частоту, равную Lo /2l2s. In кроме того, возможна продольная вибрация. Их число — dco / 2nsc. Где с-скорость продольной упругой волны. Таким образом, общее число нормальных колебаний, когда частота находится между o и co + da, равно、 Здесь C-это «средняя скорость», которая определяется соотношением.
В этом заключении мы проигнорировали анизотропию упругих свойств кристаллов, которые также встречаются в кубических кристаллах. Используя уравнение изотропного твердого тела, его упругие свойства характеризуются двумя упругими константами (например, модулем Юнга и коэффициентом Пуассона или значениями скорости c и c.). Средний «- *■+1 + I⁴, 3> установка x = La> / 0 будет выглядеть так 7⁴, — ⁴ > ⁴ , — => Интеграл справа, очевидно, a constant. In другие слова、•): ⁽1в> Поэтому, если мы введем еще 6 = kT、 ЭЭ,+ 1Т \(41.7) * ) Интеграл рассчитывается следующим образом: Куда? Поэтому, теплоемкость (41.8) (41.9) Это-закон Куба, найденного device.
Температура приближается к пуле, теплоемкость также стремится к нулю. Это исчезновение удельной теплоты при Т-0 полностью согласуется с экспериментом и нашло свое выражение в эмпирическом принципе Нернста (еще до появления теории устройства). Это уже видно из(39.4).Если он велик для каждого члена, сумма равна, поэтому E = 3 ^ 0 = 3A ^ T. In Это классическое статистическое покрытие, ¿(ω) по-прежнему определяется уравнением (41.1) (41.3) (то есть из непрерывной модели тела) также справедливо.
Правда, высокочастотные колебания, которые нельзя вычислить по непрерывной модели, уже играют свою роль, но в общей классической статистике важно рассчитывать только нормальную частоту, и это число правильно задается соотношением r (o»)= ZAG. поскольку уравнение из x (41.3>) оправдано в обоих крайних случаях (очень низкие и очень высокие температуры), вы также можете рассматривать это как интерполяцию и распространить ее на среднюю область. Выдерживая силу разума(41.6). Мы получаем Где A-постоянная решетки, в = «нет».Эластичная длина Волна, которая соответствует этой максимальной частоте Lsh1n = 1,5 А. Конечно, следует помнить, что в этом расчете будет дан только размер и попадание.
- Потому что в этих коротких волнах уравнение 2 ( ), полученное из рассмотрения сплошной непрерывной модели, уже не может дать точного результата. Я введу обозначения Tf. (41.12)) (T, называемая характеристической температурой).Затем вы можете написать(41.4) Итак, средняя энергия зависит от соотношения T / Tc. Если T больше характерной температуры T, то, другими словами, для всех собственных колебаний вплоть до наибольшей частоты、 Яш Ге * Г ’Т Если энергия мала, то их средняя энергия будет равна классическому значению kT. В этом случае значение 3§ —- Единство и близость к шагу — » * −1 Емкость-Это классическое значение ZA. In в этой области соблюдаются законы дю Рона и Пети.
И наоборот, если температура T значительно ниже характеристической температуры Tc, Интеграл (41.4) может бесконечно заменять верхний предел, в результате чего получается формула, подходящая для низких температур (41.5) и закона теплоемкости T. следовательно, чем ниже характеристическая температура T, тем шире область действия законов дюрона и Пети. Напротив, если упругая волна является быстрой, а постоянная решетки a-малым объектом, то величина a, следовательно, T, велика, и даже при комнатной температуре законы дуромонов и мешочков не выполняются (Алмаз). Формула энергетического устройства хорошо подтверждается опытом.
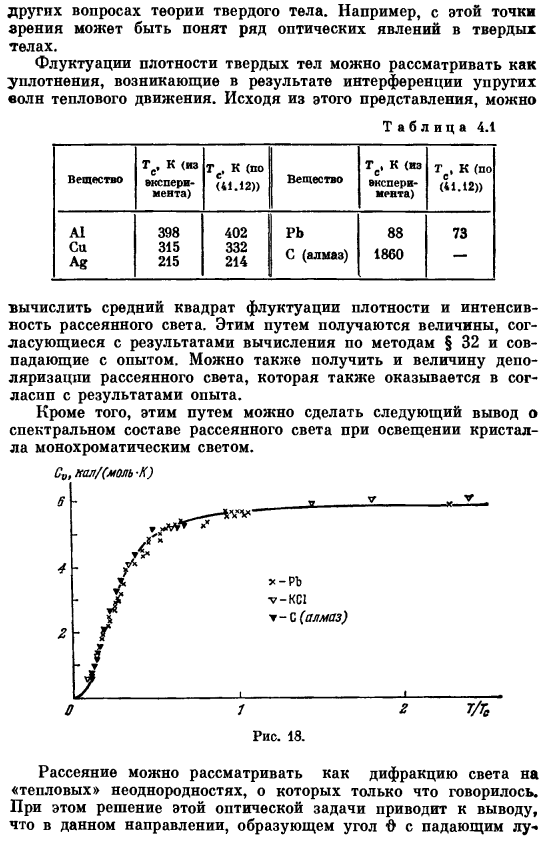
Кривая сплошной линии, прибор [формула (41.14) 1;точка-Pb, KC1, C (Алмаз) экспериментальные данные. Людмила Фирмаль
Получаем дифференциал (41.13), удельную теплоемкость Введенный здесь Интеграл грубо вычисляется. Внутри таблицы. 4.1, уравнение (41.12) и значение Т рассчитываются по экспериментальным данным теплоемкости. На рисунке 18 показано значение C, соответствующее соотношению T / T. Понятие теплового движения твердого тела как совокупности упругих волн позволяет решить не только теплоемкость твердого тела, но и очень многое Другие проблемы теории твердого тела.
Например, с этой точки зрения, многие оптические явления в твердых телах Колебания плотности твердых тел можно рассматривать как конденсацию, возникающую при интерференции упругих волн в тепловом движении. На основе представления, вы можете Падение с experience. It также возможно получить величину деполяризации рассеянного света, что также согласуется с экспериментальными результатами. Кроме того, данный метод позволяет сделать следующие выводы о спектральном составе рассеянного света при освещении кристалла монохроматическим светом. C, кал /(мм-к) Я… Два / Gs_ д — РЬг-КС! ГБ(Алмаз) г / т.» г. 1.
Рассеяние можно рассматривать как дифракцию света из-за»тепловой» неоднородности, которую мы только что получили discussed. In в этом случае решение данной оптической задачи, в данном направлении, образует падающий пучок и угол O、 Кроме того, дифракция вызвана упругими волнами, встречающимися с Брэггом conditions. In это направление, упругая волна теплового движения, направление рассеяния — направление положительного отражения от плоскости упругой волны, длина упругой волны а рассеивает свет, удовлетворяющий условию. л. (41.15) X-длина волны падающего света. Амплитуда этой рассеивающей упругой волны изменяется пропорционально cos (O + a) в зависимости от времени.
Где w-2lC1 / L (c-скорость упругой волны, то есть скорость звука).Поскольку амплитуда рассеянной световой волны пропорциональна амплитуде рассеянной упругой волны, она пропорциональна cos (ei + a).Поэтому, если частота падающей световой волны равна v = 2itV / K (V-скорость света в теле), то поле рассеянного света пропорционально ЭОС(от — | — А) cosvt = — cosvt (В + С) + а] + в COS [(в-а) т + а]. Подобный этому Рассеянный свет имеет частоту v±a. (41.15) спасибо — ^2.1 Есть 2 частоты. Угол О, включая Результирующее изменение частоты при молекулярном рассеянии очень мало. Например, для Кристалла частота изменяется примерно на 2 минуты (1 минуту) от его размера.
Смотрите также:
| Теория теплоемкости твердых тел | Кристаллы со сложной структурой элементарной ячейки |
| Колебания одномерной цепочки упругосвязанных частиц | Равновесное излучение. Формула Планка |

