Оглавление:
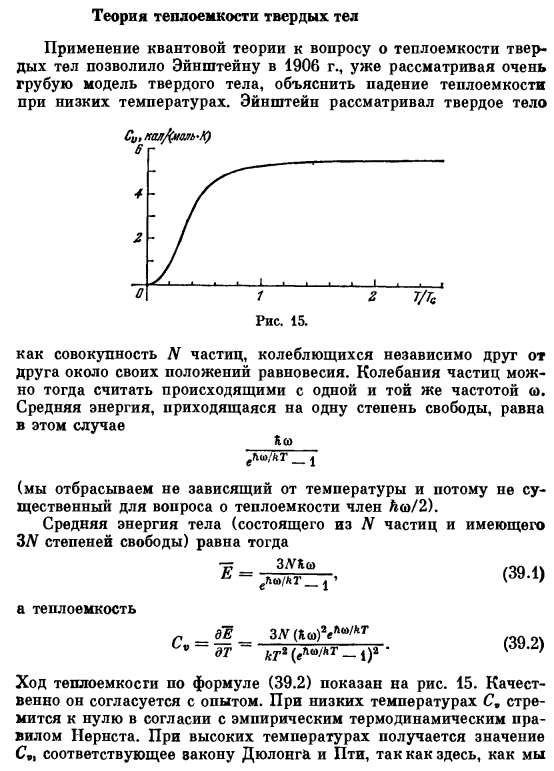




Теория теплоемкости твердых тел
- С применением квантовой теории к проблеме теплоемкости твердых тел, в 1906 году Эйнштейну удалось объяснить снижение теплоемкости при низких температурах, принимая во внимание уже очень грубые модели твердых тел. Эйнштейн увидел твердое тело Рис.15. Потому что множество частиц, которые колеблются независимо, дрейфуют друг с другом вокруг своего равновесия position. It можно предположить, что вибрация частиц происходит на частоте.
В этом случае средняя энергия на обод равна (Термин Лш/ 2 отбрасывается, но это не критично для проблемы теплоемкости, поскольку он не зависит от температуры.) Средняя энергия тела (состоящего из N частиц, имеющих 3 степени свободы) равна (39.1) Теплоемкость Де _ F в (39.2) Ход теплоемкости Формула(39.2) приведена на рисунке. 15.Качество Experience. At низкие температуры、 Он стремится к нулю в соответствии с эмпирической термодинамикой Периста rules.
Энергия является формой 2-го порядка от составляющей смещения всех частиц, а сила, действующая на частицы, является равномерной линейной функцией смещения всех частиц. Людмила Фирмаль
Высокие температуры, соответствующие значения C получены для Дюрона и Пети вакоп. Как видно, барное выражение энергии осциллятора становится классическим. Однако согласие с опытом носит качественный характер. Формула (39.2), при 7 = 0, дает бесконечно более высокий порядок касания кривой теплоемкости. Опыт показывает, что снижение теплоемкости происходит чаще rapid. In кроме того, постоянная ω определяется чисто эмпирически, и в природе нет такой собственной частоты. Таким образом, этот результат заставил нас думать, что введение квантовых понятий может объяснить температурную зависимость теплоемкости, но было ясно, что необходимо решить проблему более совершенной модели тела.
Это было сделано устройством в 1912 году и родилось вместе с Кальманом*). § 18 рассмотрим твердое тело как систему из N частиц, которые связаны между собой квазиупругими силами и колеблются вокруг положения равновесия. При введении обычных координат энергия системы Е может быть представлена как сумма энергий резонаторов, соответствующих отдельным нормальным колебаниям. (Их число равно З/У-6 = = » ZAG-число степеней свободы). средняя энергия нормального колебания с частотой, равной w, задается формулой планка е.
Таким образом, средняя энергия тела равна Здесь£,= 2Aa> | / 2- «нулевая энергия», энергия при температуре абсолютной zero. As уже упоминалось, что она не играет роли в вопросе теплоемкости, но, например, если амплитуда колебаний велика, в зависимости от температурной зависимости рассеяния рентгеновского излучения на твердом теле, то эта энергия будет больше.
- Если число нормальных колебаний на частотах меньше обозначается 2(o), то число нормальных колебаний на частоте интервала (w, o + «1sh) будет равно 2 (w).Количество входящих ) Более подробное описание M. It предлагается в книге Борна: И. Борн, М. И… Перт-Майер М. Теория Твердого Тела: Пер. С ним, — М.; Л.: ОНТИ, 1938, см.: Гельцфельд К. Ф. теория твердого тела: Пер. С ним. Л.: ОНТИ、 Выражение (39.4) можно заменить целым числом.) Так…
Где o> ty-максимальная частота нормальной vibration. It определяется из соотношения 2 (av»)= 3 ^(39,6) Потому что общее число нормальных колебаний равно ZN. Уравнения (39.4) и (39.5) показывают, что для решения задачи об энергии твердого тела с помощью квантовой статистики необходимо знать собственную частоту нормальной вибрации, но для решения той же задачи в классической статистике не требуется знание частоты нормальной вибрации-средней энергии, при которой число степеней свободы зависит только от no.
Очень трудно полностью рассчитать все собственные частоты трехмерного твердого тела. Людмила Фирмаль
Однако решение задачи теплоемкости при низких температурах упрощается для следующих ситуаций: при низких температурах это будет показано на рисунке 1.In в уравнении средней энергии (39.4), при 13 частотной зависимости функции планка, важны только члены, соответствующие низким частотам нормальных колебаний. Перемещение частиц при определенной нормальной вибрации можно считать стационарной волной перемещения внутри тела. Низкочастотные колебания соответствуют волнам, которые имеют большую длину по сравнению с постоянной решетки тела.
Это означает, что эти упругие колебания являются акустическими (и ультразвуковыми) колебаниями, и если рассматривать тело можно считать непрерывным, а для вычисления его собственной частоты использовать теорию упругости непрерывного solid. To представьте себе связь между колебаниями непрерывного твердого тела и дискретного Кристалла, рассмотрим 1-мерный Кристалл model. In в этом случае проблема может быть решена точно.
Следует также отметить, что с точки зрения классиков рассмотрим имущественный вопрос. применяя условие, как представляется, несовместимы Трахать. x Кристалл мы-раса механиков. Может быть статистика, другое Чтобы сформировать, заменив все Обычный Классический случай. Во-первых, мы опишем решения проблемы теплоемкости, описанные выше.
Смотрите также:

