Теория прочности. Основные понятия
Общие сведения о расчетах на прочность. Одной из важнейших задач инженерного расчета является оценка прочности детали по известному напряженному состоянию в опасной точке поперечного сечения. Для простых видов деформаций эта задача решается сравнительно просто: по известным формулам определяют максимальные напряжения, которые затем сравнивают с опасными (предельными) для данного материала напряжениями, устанавливаемыми экспериментально. При этом прочность детали считается обеспеченной, если максимальные напряжения не превышают предельных значений. В случае необходимости реализовать требуемый коэффициент запаса прочности максимальные напряжения сравнивают с допускаемыми.
Указанный подход к оценке прочности является вполне обоснованным, так как при растяжении и сжатии бруса имеет место однородное линейное напряженное состояние, а при прямом поперечном изгибе наиболее нагруженные точки также находятся, как правило, в условиях линейного напряженного состояния.
Для сложного напряженного состояния подобный метод оценки прочности непригоден. Дело в том, что для одного и того же материала, как показывают опыты, опасное состояние может наступить при различных предельных значениях главных напряжений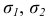 
и 
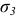в зависимости от соотношений между ними. Поэтому экспериментально установить предельные величины главных напряжений очень сложно не только из-за трудности постановки опытов, но и вследствие большого объема испытаний. В случае сложного напряженного состояния конструкции рассчитывают на прочность, как правило, на основании теоретических разработок с использованием данных о механических свойствах материалов, получаемых при испытании на растяжение и сжатие (иногда используют также результаты опытов на кручение). Только в отдельных случаях для оценки прочности конструкции или ее элементов прибегают к моделированию. В исключительных, особо ответственных случаях вопрос о прочности решается натурными испытаниями опытных образцов конструкции.
Все существующие теоретические методы расчета основаны на гипотезах о преимущественном влиянии того или иного фактора на процесс перехода материала в предельное состояние. Суть применения этих гипотез для оценки прочности материала заключается в замене фактического напряженного состояния равноопасным (эквивалентным) ему линейным напряженным состоянием. Равно-опасными называют такие напряженные состояния, у которых при пропорциональном увеличении напряжений одновременно наступает предельное состояние.
Приведение сложного напряженного состояния к равноопасному ему линейному осуществляется заменой главных напряжени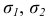й и 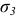эквивалентным напряжением, которое надо создать в растянутом образце, чтобы получить напряженное состояние, равноопасное заданному. Прочность оценивают при помощи сравнения эквивалентных напряжений с предельными при растяжении (сжатии) или непосредственно с допускаемыми напряжениями.
Выбранную за основу гипотезу о преимущественном влиянии на прочность материала того или иного фактора часто называют теорией прочности.
Теория наибольших нормальных напряжений (первая теория прочности). Согласно этой теории преимущественное влияние на прочность оказывает величина наибольшего нормального напряжения. Предполагается, что нарушение прочности в общем случае напряженного состояния наступит тогда, когда наибольшее по абсолютной величине нормальное напряжение достигнет значения, соответствующего предельному состоянию данного материала при простом растяжении или сжатии.
Условие прочности можно записать в следующем виде:
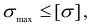
где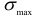 
— величина наибольшего по абсолютному значению главного напряжения для исследуемого напряженного состояния; 
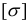— допускаемое напряжение, принимаемое для одноосного растяжения или сжатия.
Для пластичных материалов рассматриваемая теория прочности опытами не подтверждается. Она дает удовлетворительные результаты лишь для весьма хрупких материалов (например, кирпич, камень и т. п.) при условии, что наибольшее нормальное напряжение — растягивающее.
Теория наибольших линейных деформаций (вторая теория прочности). Согласно этой теории основной причиной разрушения материала является наибольшая относительная линейная деформация. Предполагается, что нарушение прочности в общем случае напряженного состояния наступит тогда, когда наибольшая по абсолютной величине линейная деформация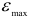 
достигнет опасного значения, соответствующего предельному состоянию данного материала при растяжении или сжатии.
Условие прочности в рассматриваемом случае записывается так:
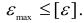
Используя формулы (2.17) [13] обобщенного закона Гука, выразим условие прочности (2.90) в напряжениях. Так как из трех деформаци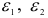й 
и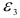 
наибольшей в алгебраическом смысле будет деформация 
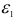, то
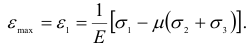
Имея в виду, что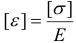 
окончательно получим
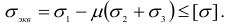
Из условия прочности (2.91) видно, что с допускаемым напряжением нужно сравнивать не какое-либо из главных напряжений, а их комбинацию, которая представляет собой некоторое напряжение, называемое эквивалентным, или приведенным.
Вторая теория учитывает влияние на прочность всех трех главных напряжений, однако опытами она подтверждается только для хрупких материалов (например, для легированного чугуна, высокопрочных сталей после низкого отпуска и т. д.).
Теория наибольших касательных напряжений (третья теория прочности). В качестве фактора, определяющего прочность материала, здесь принимается величина наибольшего касательного напряжения. Предполагается, что предельное состояние в общем случае напряженного состояния наступит тогда, когда наибольшее касательное напряжение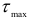 
достигнет опасного значения, соответствующего предельному состоянию данного материала при растяжении.
Условие прочности имеет вид
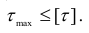
Поскольку, согласно (2.25),
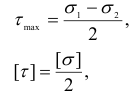
то условие прочности (2.90) окончательно можно записать так:
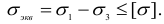
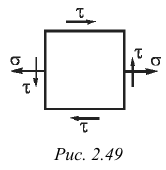
Рассмотрим часто встречающийся на практике случай плоского напряженного состояния (рис. 2.49), для которого
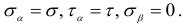
Тогда, на основании формулы (2.22)
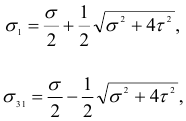
и условие прочности (2.93) можно записать в следующем виде:
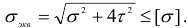
Третья теория прочности хорошо подтверждается экспериментальными данными для пластичных материалов. Недостатком ее является то, что она не учитывает величину главного напряжения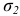 
, которое также оказывает некоторое влияние на прочность материала. Кроме того, третья теория прочности неприменима при расчете деталей из хрупких материалов.
Энергетическая теория формоизменения (четвертая теория прочности). В качестве критерия прочности в данном случае принимается количество удельной потенциальной энергии формоизменения, накопленной деформированным элементом. Согласно этой теории переход материала в предельное состояние в общем случае напряженного состояния произойдет тогда, когда величина удельной потенциальной энергии формоизменения достигнет значения, соответствующего предельному состоянию данного материала при растяжении. Условие прочности имеет вид
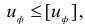
где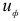 
— удельная потенциальная энергия формоизменения, определяемая выражением (2.28).
Выразив 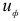и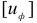 
через главные напряжения, окончательно получим
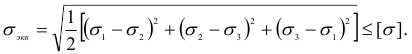
Для частного случая плоского напряженного состояния, рассмотренного выше (см. рис. 2.49), условие (2.95) принимает вид
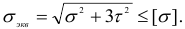
Энергетическая теория прочности дает для пластичных материалов более точное, по сравнению с третьей теорией, совпадение теоретических расчетов с экспериментальными данными, благодаря чему она получила большое распространение. Для расчета деталей из хрупких материалов данная теория прочности неприменима.
Теория прочности Мора (пятая теория прочности). Согласно этой теории, единого критерия прочности, общего для всех видов напряженного состояния, не существует. В каждом случае прочность материала зависит от величины и знака наибольших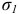 
и наименьших 
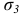главных напряжений; напряжение 
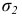на прочность материала влияет незначительно и им можно пренебречь. Условие прочности записывается в следующем виде:
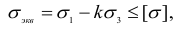
где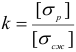 
— коэффициент, учитывающий различную способность материала сопротивляться растяжению и сжатию; 
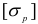и 
— допускаемые напряжения соответственно на растяжение и сжатие.
Для пластичных материалов, у которых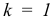 
, теория прочности Мора дает результаты, совпадающие с третьей теорией. Эту теорию в настоящее время широко применяют при расчете на прочность деталей из хрупких материалов. Недостатком ее является то, что здесь не учитывается влияние на прочность главного напряжения .
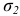Оценивая рассмотренные выше теории прочности, следует указать на то, что в практических расчетах используют в настоящее время для пластичных материалов третью или четвертую теории, а для хрупких материалов — теорию прочности Мора.
Эта теория взята со страницы лекций по предмету «прикладная механика»:
Возможно эти страницы вам будут полезны:
| Расчеты на прочность и жесткость |
| Напряженное состояние и разрушение при кручении |
| Косой изгиб: определение, пример, формулы |
| Изгиб с растяжением (сжатием) |
