Оглавление:





Теория пограничного слоя. Задачи
- Построение линии потока в том случае, если полная жидкость обтекает цилиндр. Выполните шаги в этой последовательности, используя требуемое соотношение в Примере 4-2 и нарисуйте диаграмму обтекания, когда она обтекает цилиндр, выполните следующие действия: a) установите значение T = C (то есть выберите линию потока). Б) построить значение Y = C + K-линии, параллельные оси X и Y = K (X + Y») — окружность радиуса«/, X, касаясь оси X сначала Отметьте пересечение линий и окружностей, построенных для (Pb) d) соедините эти точки на графике, чтобы получить линию потока V = C. l) выберите другое значение C и повторите приведенную выше конфигурацию, чтобы найти новую линию потока.
Приводить в движение. Сравните значения ввода-вывода, найденные в выражении (4.13), с соответствующими значениями, полученными в выражении(4.106).Следующее значение y / y равно 4хе: а) 0,2; Б) 0,5; в) 1,0.Выразите результат в процентах от погрешности определения локальной скорости. Ответ: а) 4-1. 5%; б) — | −2,5%; в) −26%. 4-3.Нестационарный поток псевдо-пластина жидкости вблизи подвижной стенки. Расширяется область вычислений в Примере 4-1 для характеристики нестационарного течения псевдопластической жидкости вблизи плоскости, которая начала внезапно двигаться.
Высокий уровень турбулентности в приближающемся потоке увеличивает не только средний коэффициент переноса тепла, но также и локальный перенос тепла на верхней части цилиндрической. Людмила Фирмаль
Пожалуйста, объясните, почему использование модели Оствальда-Вейля (1.9) — закон мощности (4.128) В том же профиле скорости (h), что и в Примере 4-1. 。 Вскоре появилось название Кармановской интегральной связи. Для профиля посунола, используя формулу (4.125), получаем: а)формулу (4.121)、 Рассчитайте толщину пограничного слоя. b) формула (4.123) Сопротивление вдыи на плоской плите.
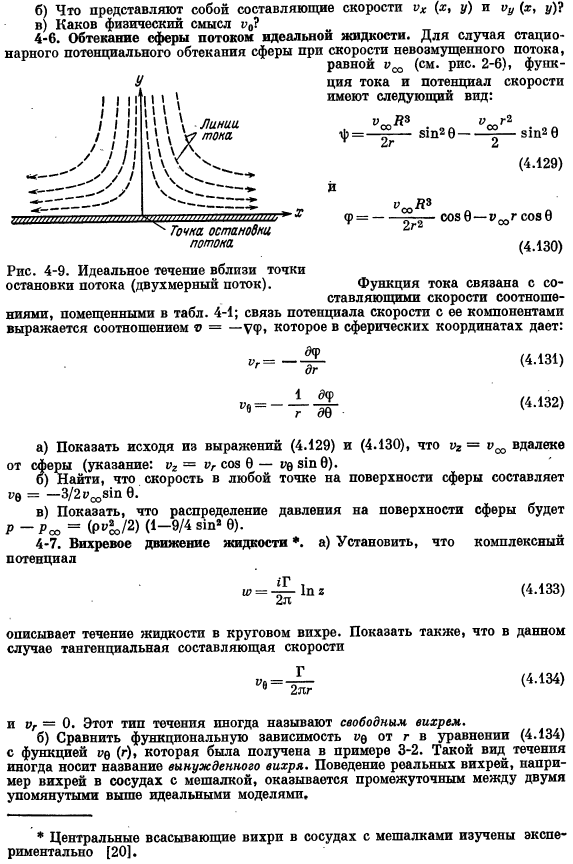
В плоскости «потенциал» можно описать поток> = — отт*приблизительно > 1, которому принадлежит точка остановки потока(рис.4-9). б) каковы составляющие скорости o *(i, y) и («, p)? 4-6.Идеальный поток жидкости обтекает сферу. Для стационарного потенциального обтекания сферы с неоперационной скоростью, равной 2-6 (см. рис. 11), функция потока и потенциал скорости I / 11I’.Существуют следующие формы: P = — soy 0 — UTG SOV 0 Конец(4.130) Цифры 4-9.Идеальный поток вокруг точки остановки потока(2-мерный поток).Текущие функции включают в себя Установите коэффициент скорости, который находится в таблице.
Связь между потенциалом скорости и его компонентами выражается соотношением o = — RF, в сферических координатах: (4.131) (4.132) с) показывают, 1 Р » В^₽ — / 2⁾ Далеко Интегрированный Е: «Р =скорость Из формул (4.129) и (4.130), 0-1> e 81n 0). Поверхность шара является Объясните поток жидкости Круговые вихри. Шоу. Также Этот. Дело танго! (4.134) И o,=0.Этот тип течения иногда называют свободным вихрем. Б) сравните функциональную зависимость e от r в выражении (4.134) с функцией Pe (g), полученной в Примере 3-2.Этот тип течения иногда называют вынужденным вихрем. Поведение реального вихря, например, вихря в сосуде с мешалкой, является 2-в-одном. Центральная концентрация[20].
- Вихрь в сосуде. Формула (4.1!ПП = В?- РУТЕНИЙ)объявления > АР О К ’ & 1 Уравнение в пористой среде(4.137). Как? Несжимаемый (корпус 1) t = 0; 6 = 0 Сжимаемый (случай 2) u ^ ^ 0;₽= 0 Изотермическое Расширение (Случай 3). 。 Развертывание изоляции (случай 4). 。 。 Показано уравнение из 4 перечисленных случаев (4.137) (’»+1) Ваш> $ / » 2С.₌r2₀ ки+ + т) / к Д1 Н Члены, которые принимают во внимание влияние сил, игнорируются. Это потому, что Опио мал в этом отношении. * Эмпирическая модификация закона Дарси была предложена Бринкманом[24]: 0 = — рр-xoo + рузсо + ру (4.136 а) Для ограничения деформации профиля скорости генока была введена пористая среда.
Давление. При рассмотрении терминов, включающих гравитационное ускорение, тепловые или диффузионные уравнения, Случай 1 является уравнением Лапласа, случай 2 нелинейен, а Случай 3 и 4 нелинейны 4-9.Радиальное течение через пористую среду (рис. 4-10).Жидкость протекает через пористую цилиндрическую оболочку, внутренний и внешний радиусы которой равны g и gg соответственно. Значения давления для этих поверхностей известны, q и p₂.Длина цилиндрической оболочки равна L. а) найти распределение давления потока несжимаемой жидкости, радиальную скорость потока, объемный расход/). Пористый Среда. Жадность окружающей среды.
Значения критериев Нуссельта и Рейнольдса вычислены по диаметру трубы как определяющему отрезку и скорости потока до встречи с трубой как определяющей скорости. Людмила Фирмаль
Скорректировать результаты, полученные в случае течения сжимаемой жидкости и идеального газа. П-П1, 1 ПГ / ГД Р2-R11PG₂/ Г1 п «(пр-П1) * 1и-1arg / П1 2lKL (пр-P₁) Н 1П (’- г / н) б) 2yaky(РГ-Р1)₽Н> 11п(ый / Г1) LHY(Р. — Р1)IR11p(ый / Г1) 4-10.Используйте метод, описанный в нестационарном потоке а) пример 4-2 в кольцевом зазоре, чтобы получить тот же зазор, полученный в этом примере. Сравните полученные результаты с уже известными решениями[25]. Б) для I 3 0, если жидкость неподвижна, и 1> 0, если внешний цилиндр вращается с угловой скоростью 2, найти решение нестационарного тангенциального течения в коаксиальном кольцевом зазоре. Это приводит к разрешению tvh°e [26]^°.
Сравните ваши результатыс ранее опубликованными результатами 4-11.Поток через пористую среду, расположенную в трубе, а) труба радиуса I заполнена определенным количеством пористого материала по всему объему. Застойная среда с учетом того, что скорость стенки трубы равна скорости пули. б) записывает формулу объемного расхода в виде произведения поправочного коэффициента с учетом расхода, рассчитанного в соответствии с законом Дарси и «эффектом стенки». в)»в» указывает, что результаты, полученные в пункте, упрощены до конкретного случая, а»в» определяет, является ли поправочный коэффициент, найденный в пункте, важным в обычных условиях промышленных расчетов.
Д является ли указанный поправочный коэффициент большим или меньшим, чем поправка, необходимая для учета нарушения однородности слоя 1 стенки трубы? Рядом сопел От U\ Я 1о(я! Великобритания)) Вид в поперечном разрезе. исходя из y, это символ ethepar (d = — uv), который называет meaada любыми 2 точками. g к YO1 Не вид 154ТрпокаХ °твтв (о. юч), чтобы показать его на стационарном мобильном телефоне、 Если внешняя сила имеет па, уравнение движения может быть интегрирован! 1 и 2 4 «(4-4)+ В ± (ФА-ФГ)= 0(4.143) То есть»taggo’yakGsamoe’vy⁶^».^ avaennesh BeRnUlli-тогда может быть стационарное невязкое движение(т. е. поток между 2 точками 1 и 2 находит уравнение Бернулли в случае 7.3.
Смотрите также:
| Установившееся двухмерное потенциальное течение | Пульсационные и средние по времени значения скорости |
| Теория пограничного слоя | Осреднение по времени уравнений сохранения для несжимаемой жидкости |

