Теория двойственности и недифференциальные условия оптимальности в задаче выпуклого программирования
В задачах математического программирования (1.4)—(1.6) можно указать условия оптимальности, не прибегая к понятиям производных и градиентов, с помощью так называемой теории двойственности. Особенно плодотворен этот подход в задачах выпуклого программирования.
Будем рассматривать функцию Лагранжа (1.7). Обозначим через 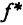 точную нижнюю грань целевой функции задачи (1.4)—(1.6) на ее допустимом множестве
точную нижнюю грань целевой функции задачи (1.4)—(1.6) на ее допустимом множестве 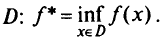 . Точка
. Точка 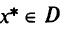 является решением задачи (1.4)-(1.6) в том и только в том случае, если
является решением задачи (1.4)-(1.6) в том и только в том случае, если 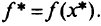 .
.
Введем вектор 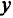 с координатами
с координатами
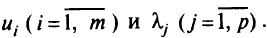
Вектор 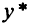 называется вектором Куна-Таккера задачи (1.4)—(1.6), если при всех
называется вектором Куна-Таккера задачи (1.4)—(1.6), если при всех 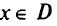
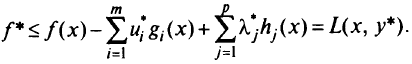
Любой задаче математического программирования можно поставить в соответствие так называемую двойственную задачу оптимизации. Между прямой и двойственной задачами имеются полезные связи.
Двойственной к задаче (1.4) — (1.6) называют задачу
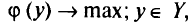
где
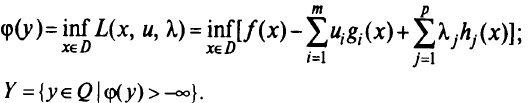
Рассмотрим подробнее задачу линейного программирования
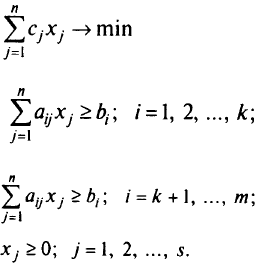
Переменные 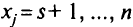 могут иметь любые значения. Функция Лагранжа этой задачи
могут иметь любые значения. Функция Лагранжа этой задачи
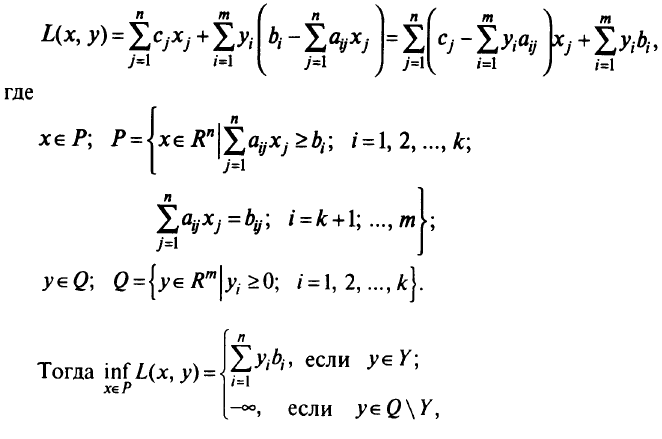
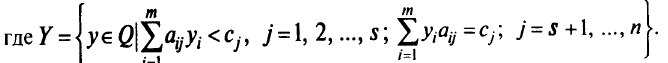
Согласно определению двойственности, двойственной задачей к исходной задаче является следующая:
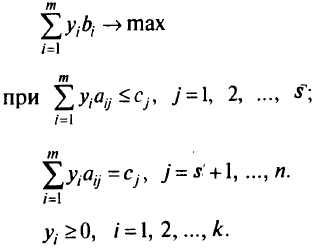
Исходную задачу называют прямой. Если целевую функцию в двойственной задаче 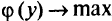 заменить на —
заменить на —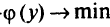 , то можно утверждать, что задача, двойственная к произвольной задаче математического программирования, всегда выпукла. Если в задаче математического программирования множество замкнуто и выпукло, функции
, то можно утверждать, что задача, двойственная к произвольной задаче математического программирования, всегда выпукла. Если в задаче математического программирования множество замкнуто и выпукло, функции 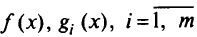 , непрерывны и выпуклы на
, непрерывны и выпуклы на 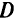 , функции
, функции 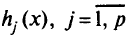 линейны или отсутствуют и решение прямой задачи конечно
линейны или отсутствуют и решение прямой задачи конечно 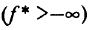 , в частности она имеет решение, то множество решений двойственной задачи непусто и совпадает с множеством векторов Куна-Таккера прямой задачи. При этом справедливо соотношение двойственности
, в частности она имеет решение, то множество решений двойственной задачи непусто и совпадает с множеством векторов Куна-Таккера прямой задачи. При этом справедливо соотношение двойственности 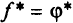 , т.е. минимум целевой функции прямой задачи совпадает с максимумом целевой функции двойственной задачи. Учитывая, что число переменных в двойственной задаче равно числу условий-ограничений в прямой задаче, в ряде случаев двойственную задачу решить проще.
, т.е. минимум целевой функции прямой задачи совпадает с максимумом целевой функции двойственной задачи. Учитывая, что число переменных в двойственной задаче равно числу условий-ограничений в прямой задаче, в ряде случаев двойственную задачу решить проще.
Получим необходимые и достаточные условия оптимальности в задаче выпуклого программирования на основе теории двойственности. В этом случае изменится только форма необходимых и достаточных условий (не будут участвовать производные), но предпосылки в обоих случаях будут одинаковы.
Для примера рассмотрим задачу квадратического программирования:
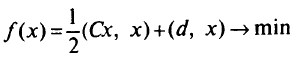
при
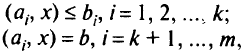
где 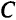 — положительно определенная симметрическая матрица размерностью
— положительно определенная симметрическая матрица размерностью
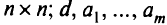
заданные векторы из
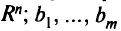
заданные числа.
Функция Лагранжа задачи
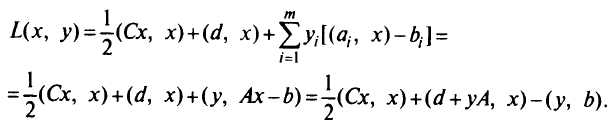
Задача, двойственная к исходной
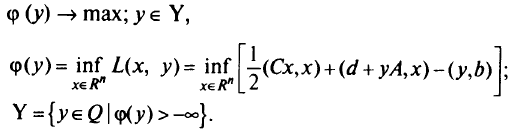
Для положительно определенной матрицы Спроизводная функции Лагранжа
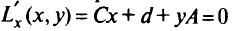
в точке
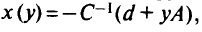
и двойственная задача записывается в виде
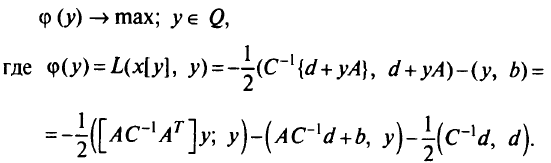
Полученная функция квадратична — условия неотрицательности относятся к первым к переменным. Решить двойственную задачу гораздо проще. Если же в исходной задаче нет ограничений неравенств, то двойственная задача приводит к безусловной оптимизации квадратичной функции.
Пара 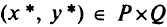 называется седловой точкой функции
называется седловой точкой функции
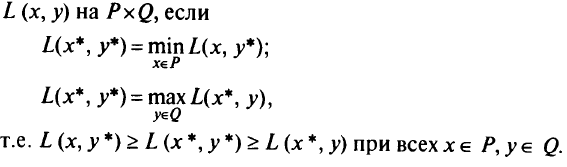
Тогда точка 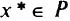 является решением прямой задачи в том и только в том случае, если существует вектор
является решением прямой задачи в том и только в том случае, если существует вектор 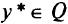 такой, что пара
такой, что пара 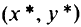 — седловая точка функции Лагранжа
— седловая точка функции Лагранжа 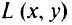 на
на 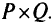 . Таким образом, если одновременно решать и прямую и двойственную задачи, то к точке минимума (т.е. к решению) мы можем приближаться с двух сторон.
. Таким образом, если одновременно решать и прямую и двойственную задачи, то к точке минимума (т.е. к решению) мы можем приближаться с двух сторон.
Вектору Куна-Таккера часто придают экономические интерпретации. Рассмотрим две из них. Пусть предприятие выпускает некую продукцию и стремится получить максимальный доход. Условия-ограничения в виде неравенств характеризуют затраты ресурсов при выпуске продукции. Очевидно, что в процессе ее выпуска один или несколько ресурсов будут исчерпаны полностью. Для нас это активные ограничения. Другая часть ресурсов будет не использована (пассивные ограничения). В двойственной задаче (согласно условию дополняющей нежесткости) для активных ограничений множители
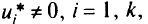
а для пассивных ограничений
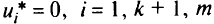
(эти ресурсы недефицитны). То есть предприятию следует закупать в первую очередь те ресурсы, для которых
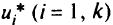
имеют наибольшее значение. Если же есть возможность увеличивать количество всех ресурсов сразу, то их желательно приобретать в пропорциях, описываемых вектором Куна-Таккера.
В иной интерпретации предприятие хочет продать «ненужную» часть сырья и установить за него такую цену, чтобы максимизировать общий доход. Пусть вектор с — заданный вектор цен на сырье. Предприятие стремится продать сырье по таким ценам, чтобы получить такую же прибыль, как в случае, когда из проданного сырья изготовлена продукция, а для этого цены с должны быть назначены равными координатам вектора Куна-Таккера 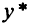 .
.
Эта теория взята со страницы лекций по предмету «математическое программирование»:
Предмет математическое программирование
Возможно эти страницы вам будут полезны:

