Теоремы об эквивалентности пар
Теорема 1. Всякую пару, не изменяя ее действия на абсолютно твердое тело, можно заменить другой парой, расположенной как угодно в той же плоскости и имеющей одинаковое с данной парой направление вращения и равный по абсолютной величине момент.
Доказательство. Пусть на тело действует пара
с плечом
Приложим к точкам
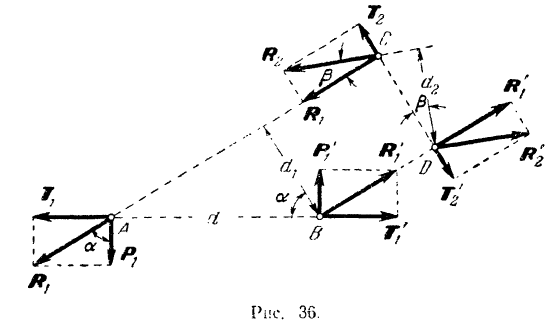
 и
и 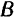 две равные по модулю и направленные но одной прямой в противоположные стороны силы
две равные по модулю и направленные но одной прямой в противоположные стороны силы 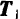 и
и 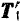 . Складывая попарно силы
. Складывая попарно силы 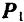 и
и 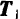 и силы
и силы 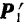 и
и 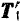 , мы, очевидно, придем к новой паре
, мы, очевидно, придем к новой паре 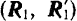 .Так как система сил
.Так как система сил 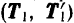 — уравновешенная, то полученная пара
— уравновешенная, то полученная пара 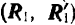 эквивалентна данной.
эквивалентна данной.
Если перенести силы этой пары в любые другие две точки, лежащие на линиях их действия (например,  и
и 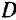 , рис. 36) и вновь присоединить к силам данной пары любую уравновешенную систему сил
, рис. 36) и вновь присоединить к силам данной пары любую уравновешенную систему сил 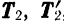 то вновь будет получаться пара
то вновь будет получаться пара 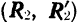 , эквивалентная данной:
, эквивалентная данной:
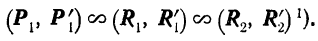
Нетрудно убедиться в том, что все полученные эквивалентные пары имеют одинаковое направление вращения (в данном случае противоположное ходу стрелки часов) и одинаковый по абсолютной величине момент.
В самом деле, как это видно из рис. 36,
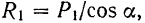
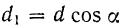
и, следовательно
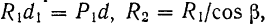
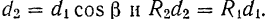
Переносом сил пары по линиям их действия и повторением операций, подобных сделанным выше, можно, очевидно, перенести пару в любое положение в плоскости ее действия и любым образом изменять модули сил пары. При этом будет соответственно изменяться длина плеча пары, но модуль момента пары и направление ее вращения будут оставаться неизменными.
Как показывает опыт и как это доказывается в динамике, пара сил, как бы она не была расположена, всегда сообщает свободному телу вращение вокруг оси, проходящей через центр тяжести тела и перпендикулярной плоскости действия пары.
Нужно заметить, что перенос пары в ее плоскости действия, так же как и перенос силы по линии ее действия, безоговорочно применим лишь для абсолютно твердого тела. Мы можем пользоваться этим свойством пары при решении задач на равновесие внешних сил, приложенных и к деформируемому телу, так как это равновесие не нарушается от того, что такое тело станет абсолютно твердым (принцип отвердевания). Но деформация тела и возникающие в результате ее в теле внутренние силы, противодействующие этой деформации, зависят от места расположения пары, и поэтому в задачах сопротивления материалов всегда указывают сечение тела, на которое действует пара.
На рис. 37 в качестве примера изображены две балки, заделанные одним своим концом в стену и нагруженные парами. Ясно, что пара, приложенная к концевому сечению (рис. 37, о), будет деформировать (изгибать) всю балку, тогда как пара, приложенная к среднему сечению (рис. 37,6), будет изгибать только левую часть балки.
Теорема 2. Не изменяя действия пары на твердое тело, ее можно переносить в любую плоскость, параллельную плоскости действия данной пары.
Доказательство. Пусть на тело действует пара 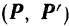 с плечом
с плечом 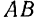 , лежащая в плоскости
, лежащая в плоскости 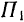 (рис. 38).
(рис. 38).
Предположим, что мы хотим эту пару перенести в какую-либо другую плоскость 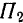 , связанную с данным телом и параллельную плоскости
, связанную с данным телом и параллельную плоскости 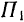 . Возьмем в плоскости
. Возьмем в плоскости 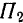 отрезок
отрезок 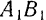 и равный и параллельный отрезку
и равный и параллельный отрезку
 , и приложим в точках
, и приложим в точках  и
и 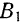 по две взаимно уравновешивающиеся силы
по две взаимно уравновешивающиеся силы 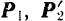 и
и 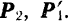 . Эти силы возьмем параллельными силам заданной пары и равными им по модулю, так что
. Эти силы возьмем параллельными силам заданной пары и равными им по модулю, так что
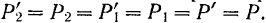
Так как добавленные силы взаимно уравновешиваются, то получившаяся система шести сил 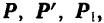
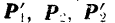 эквивалентна заданной паре
эквивалентна заданной паре 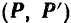 , расположенной в плоскости
, расположенной в плоскости 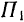 .
.
Но из новой системы шести сил четыре силы 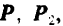
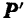 и
и 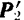 также представляют собой уравновешенную систему и потому могут быть отброшены.
также представляют собой уравновешенную систему и потому могут быть отброшены.
В самом деле, равнодействующая 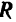 параллельных, направленных в одну сторону и равных сил
параллельных, направленных в одну сторону и равных сил 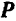 и
и 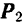 им параллельна, равна по модулю
им параллельна, равна по модулю 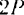 , направлена в ту же сторону и проходит через середину отрезка
, направлена в ту же сторону и проходит через середину отрезка 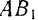 . Равнодействующая
. Равнодействующая 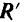 параллельных, направленных в одну сторону и равных сил
параллельных, направленных в одну сторону и равных сил 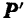 и
и 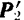 также им параллельна, равна по модулю
также им параллельна, равна по модулю 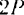 , направлена в сторону действия этих сил и проходит через середину отрезка
, направлена в сторону действия этих сил и проходит через середину отрезка 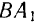 . Отрезки же
. Отрезки же 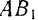 и
и 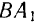 как диагонали параллелограмма
как диагонали параллелограмма 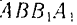 , взаимно делятся пополам в точке
, взаимно делятся пополам в точке 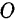 их пересечения. Таким образом, равнодействующие
их пересечения. Таким образом, равнодействующие 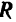 и
и 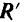 равны но модулю и направлены по одной прямой в противоположные стороны. Следовательно, эти равнодействующие взаимно уравновешиваются, и система сил (
равны но модулю и направлены по одной прямой в противоположные стороны. Следовательно, эти равнодействующие взаимно уравновешиваются, и система сил (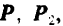 .
.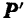
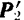 ) эквивалентна пулю.
) эквивалентна пулю.
Остаются только две силы 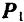 и
и 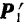 , образующие пару, которая представляет собой, очевидно, заданную пару
, образующие пару, которая представляет собой, очевидно, заданную пару 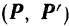 , перенесенную из плоскости
, перенесенную из плоскости 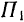 в плоскость
в плоскость 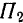 . Теорема доказана.
. Теорема доказана.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:

