Оглавление:
Теоремы о свойствах алгебраических многочленов
Пусть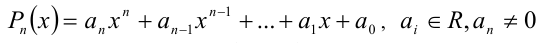 
, — алгебраический многочлен n -й степени 
.
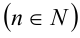Теорема 1 (о разложении многочлена произвольной степени на произведение линейных и квадратичных множителей). Многочлен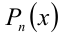 
может быть представлен единственным образом в виде произведения многочленов, степень каждого из которых не выше второй.
Теорема 2. Многочлен нечётной степени имеет хотя бы один действительный корень.
Теорема 3 (основная теорема алгебры). Многочлен n -й степени имеет ровно n корней (действительных и комплексных), в том числе действительных не больше n (сучётом их кратности).
Теорема 4. Если на концах некоторого отрезка [a, b ] значения многочлена имеют разные знаки, то на интервале (а, b) существует хотя бы один корень этого многочлена.
Заметим, что аналогичное утверждение справедливо не только для многочленов, но и для любой непрерывной на отрезке [ a,b ] функции.
Теорема 5 (условие тождественного равенства двух многочленов). Два алгебраических многочлена
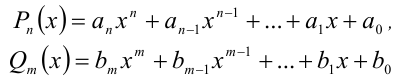
тождественно равны (т.е. равны при всех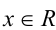 
) тогда и только тогда, когда равны степени многочленов n = m и совпадают коэффициенты при равных степенях x , т.е. 
.
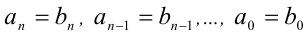Пример №169.
Определить три числа p, q и r такие, что равенство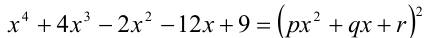 
выполняется для любого значения переменной x.
Решение:
Раскроем (вспомним соответствующую формулу сокращённого умножения) квадрат в правой части и приведём полученный многочлен к стандартному виду:
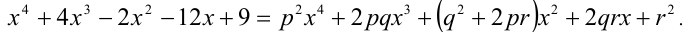
Многочлены, стоящие слева и справа от знака равенства, тождественно равны тогда и только тогда, когда выполняется система
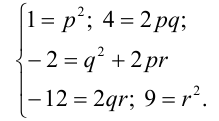
Ответ: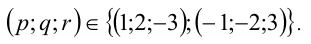 
Теорема 6. Если значения двух многочленов степени не выше n совпадают в n + 1 различных точках, то эти многочлены тождественно равны.
Например, если две параболы (графики квадратичных функций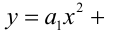 
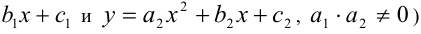пересекаются в трёх точках, то они тождественно совпадают.
Теорема 7 (формула деления многочлена на многочлен с остатком). Для любых двух алгебраических многочленов
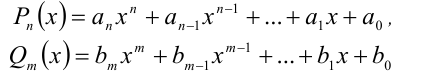
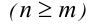найдётся единственная пара многочленов 
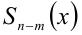и 
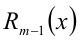таких, что справедливо тождество
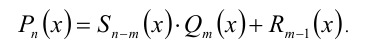
Здесь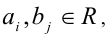 
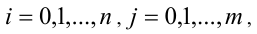
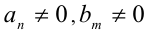, многочлен 
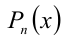называется делимым, многочлен 
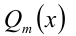— делителем, многочлен 
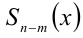— частным от деления 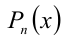) на 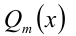, а многочлен 
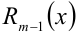(степени не выше m — 1) соответственно остатком от деления. Если 
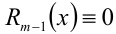, то говорят, что многочлен 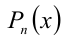делится на многочлен 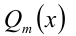нацело (без остатка).
Пример №170.
Найти остаток от деления многочлена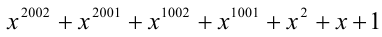 
на многочлен 
.
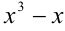Решение:
В данной задаче весьма проблематично было бы искать многочлен-остаток непосредственным делением многочлена на многочлен из-за слишком высокой степени многочлена-делимого. Запишем результат деления первого многочлена на второй в виде формулы
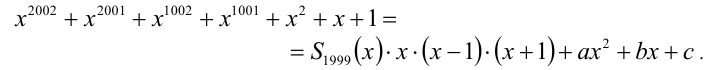
Здесь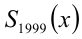 
— неполное частное от деления (неизвестный многочлен), а остаток при делении на многочлен 3-й степени может иметь максимально 2-ю степень, поэтому остаток 
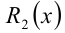выписан в общем виде как многочлен 2-й степени 
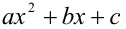. Достаточно найти значения коэффициентов a,b и c . Для этого, подставляя последовательно значения x = 0, x = 1, x = — 1 в данную формулу, получим систему
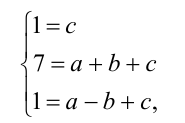
решая которую найдём искомые коэффициенты а = b = 3 , c = 1 . Поэтому остаток от деления равен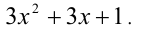 
Следующая теорема названа по имени французского математика Этьена Безу (1730-1783).
Теорема 8 (теорема Безу). Остаток от деления многочле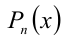на на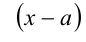 
равен значению делимого при 
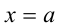(т.е.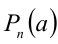 
).
Следствие. Многочлен 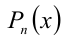делится нацело на линейный двучлен 
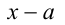тогда и только тогда, когда 
.
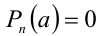Приведённое следствие из теоремы Безу во многих случаях позволяет решать целые алгебраические уравнения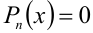 
степени выше второй. Для этого достаточно подобрать один какой-либо корень уравнения, например 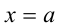, и затем поделить многочлен 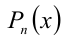на 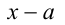. В результате получим некоторый многочлен 
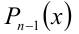степени на единицу меньше, чем n :
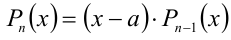, и задача свелась к решению уравнения
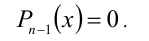
Пример №172.
Найти все значения а и b, при которых многочлен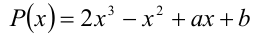 
делится нацело на многочлен 
.
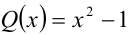Решение:
Разложим многочлен 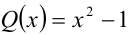на линейные множители 
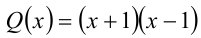. По условию, Р(х) должен делиться на Q(х), а, следовательно, Р(х) должен делиться на каждый из множителей x + 1 и x — 1. Согласно теореме Безу, это возможно тогда и только тогда, когда
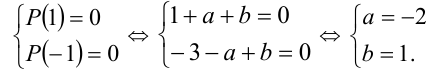
Теорема 9 (о рациональных корнях многочленов с целыми коэффи-циентами). Пусть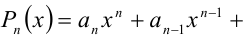 
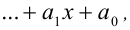
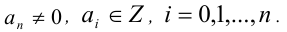Если у многочлена 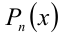) имеются рациональные корни, то все они находятся среди дробей вида p/q , где р — любой из целочисленных делителей свободного члена 
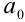, a q — любой из натуральных делителей старшего коэффициента 
.
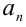Следствие. Если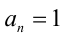 
(приведённый многочлен), то его рациональные корни следует искать среди целых делителей .
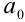Пример №173.
Решить уравнение в целых числах
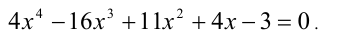
Решение:
Согласно следствию из приведённой выше теоремы, все целые корни уравнения находятся среди целых делителей свободного члена, т.е. среди чисел ± 1, ± 3 . Обозначим многочлен в левой части уравнения через f(x) . Сделаем проверку:
1) 
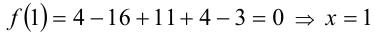является корнем уравнения;
2) 
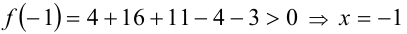не будет корнем уравнения;
3)
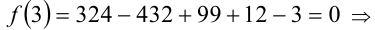нашли ещё один корень x = 3 ;
4) 
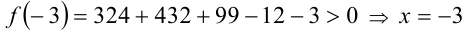не является корнем.
Ответ: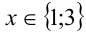
.
Пример №174.
Найти все корни уравнения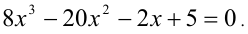 
Решение:
Не будем сразу применять указанный выше метод, а поступим следующим образом: сделаем многочлен в левой части уравнения приведённым. Для этого положим у = 2х , тогда имеем уравнение
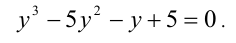
Обозначим через f(у) левую часть последнего уравнения. Свободный член в данном случае имеет 4 целых делителя ± 1, ± 5. Поскольку f( ± 1 )=0 и f(5)= 0, а больше трёх корней кубическое уравнение иметь не может, то это все корни этого уравнения. Выполняя обратную подстановку, находим соответствующие им три корня исходного уравнения.
Ответ: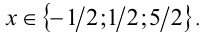 
Обратимся теперь к обобщению теоремы Виета на случай алгебраических уравнений n -й степени 
.
Теорема 10 (теорема Виета, общий случай). Пусть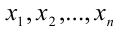 
— действительные корни алгебраического многочлена n -й степени
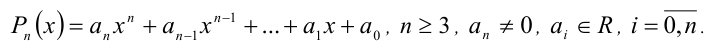
Тогда корни уравнения 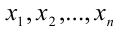связаны с его коэффициента-ми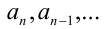 
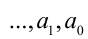посредством следующей системы равенств:
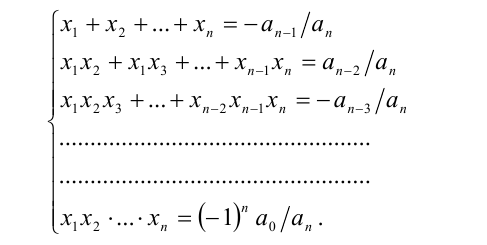
Пример №175.
Определить все значения параметра а, при каждом из которых три различных корня уравнения
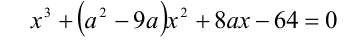
образуют геометрическую прогрессию. Найти эти корни.
Решение:
По теореме Виета для кубических уравнений
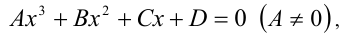
в частности, имеем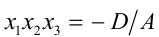 
. Для данного в условии задачи уравнения это будет выглядеть так:
Условие того, что корни уравнения образуют геометрическую прогрессию, можно записать в виде
Из (1) и (2) следует, что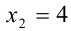 
. Таким образом, известен один из корней уравнения. Подставив это значение x в исходное уравнение, найдём теперь отвечающие ему возможные значения параметра а :
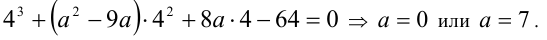
Проверка. 1) a = 0: исходное уравнение принимает вид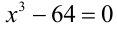 
и, очевидно, имеет три одинаковых, а не различных корня. Следовательно, это значение параметра не подходит.
2) а = 1: имеем уравнение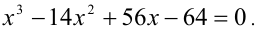 
Так как один его корень нам известен (х = 4), то, например, делением многочлена в левой части на х — 4 раскладываем многочлен на множители, приведя уравнение к виду
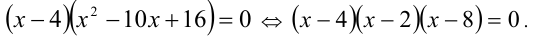
Его корни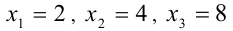 
удовлетворяют условиям задачи.
Ответ: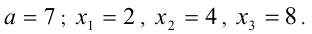 
А теперь обратимся к рассмотрению основных видов и способов решения целых алгебраических уравнений.
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:
