Оглавление:



Теоремы о взаимности работ и перемещений
- Теорема о интериорности произведений и движений Рассмотрим любую упругую систему как балку в двух состояниях. В первом состоянии (рис. 365, а) пусть обобщенная нагрузка помечена индексом / Act; смещение соответствующих точек системы будет DP, D21, DN. Второе состояние (рис. 365, Б) обойденная нагрузка, отмеченная в индексе 2, загружается в систему, и движение
соответствующих точек системы от этой нагрузки составляет D12, DGG»••>system».- П, Рис 365 рис. Триста шестьдесят шесть Существует множество возможных смещений, вызванных силой второго состояния, а смещение второго вызвано силой первого. На основе выражения первого состояния(13.33)+J — ^ — +Y-2^ -]=o, C3-3 8 ) ЛС с Дж Для второго государства +ф^^-+п -^ -]=0. (13.39)
Поскольку выражение работы внутренних сил одно и то же, то это Людмила Фирмаль
будет\уравнение, основанное на уравнениях(13.38) и(13.39 P1^12 — ^ 2 ^ 2 1 • (13.40) Выражение 371(13.40) называется взаимной теоремой работы(теорема Бетти). Она формулируется следующим образом: возможное внешнее (или внутреннее) силовое состояние 1 равно состоянию смещения 2. робот, способный перемещать внешнее (или внутреннее) силовое состояние 2. движущееся состояние 1. Когда в точках 1 и 2 в обоих состояниях системы приложена одна
обобщенная сила L=»]и P=-i, то теорема взаимности применяется к конкретному случаю нагрузки(рис. 366). Исходя из Формулы(13.40) P1^12-P2^21* И ПТ (31.41) Формула (18.41) называется обратной теоремой смещения(теорема Максвелла). Она формулируется следующим образом: под действием второй силы, которая равна смещению в ее направлении приложения второй силы, вызванной действием первой единичной силы. В общей теории исследования
- напряженно-деформированного состояния стержней, пластин, оболочек и других расчетных объектов теоремы о взаимности работ и перемещений очень сильно упрощают их применение при решении многих задач строительной механики, а также производстве экспериментов по определению движения. Используя теорему о взаимности, под действием момента M на опору определите прогиб балки D21 в середине пролета (рис. 367, а). Используя второе состояние пучка-действие в точке 2 концентрации Р(рис. 367, b) — B~ ~ и x=0 уравнение (10.65) для нахождения угла
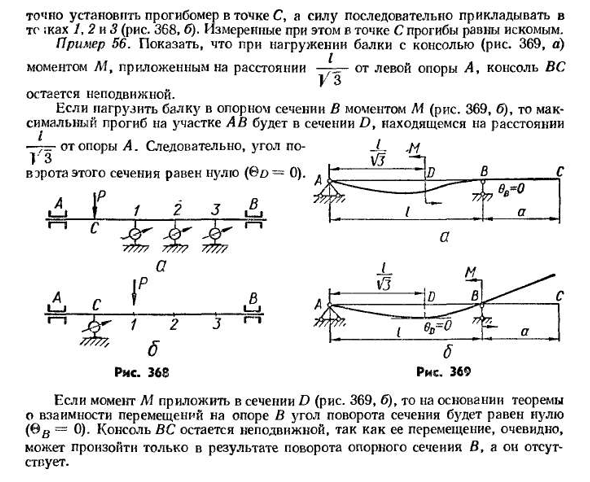
поворота опорного сечения Л Р/2 Согласно взаимной теореме работы, Откуда М Д12-Р Д21, (13.42) Пример 55. Определяет прогиб точки/, вала, нагруженного силой Р в 2 и 3 точках с(Рис. 368). Вместо этого установите дефлектор в указанной точке, как показано на рисунке. Основываясь на теореме взаимности перемещения Доста, 368, a- Прикрепите дефлектор к точке 372 С и непрерывно прикладывайте его усилие к транспортному средству. Kah1, 2, 3 (Рис. 368, б). Отклонение, измеренное в точке С, равно требуемому отклонению. Пример 56. Показано, что при загрузке балок в консоль (рис. 369, а) в момент, когда АФ прикладывается к дальней y-левой опоре из 4, консоль самолета остается неподвижной. При нагружении балки до основания сечением 100 метров(рис.
Опоры от А-369, 6), то максимальным прогибом участка А Б будет участок р, Людмила Фирмаль
расположенный на расстоянии −7=7. Таким образом, угол наклона- 1 3 Верота в этом разделе равна нулю (0/e=0). Если момент L-1 приложен, то » раздел D (фиг. 369, б), исходя из теоремы о взаимности смещения на опоре при угле поворота сечения, становится равным нулю(b#=0). Солнечная консоль остается неподвижной, так как ее движение может, по-видимому, возникнуть только в результате вращения опорного участка В, и его не существует.
Смотрите также:
| Работа внутренних сил | Общая формула для определения перемещений. метод мора |
| Применение начала возможных перемещений к упругим системам | Перемещения, вызванные действием температуры |

