Оглавление:


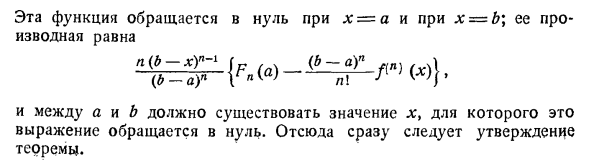


Теоремы о среднем высших порядков
- Средняя теорема высшего порядка. В §126, если f (x) является непрерывным относительно a ^ x ^ b и существует производная в интервале a <^ x <b%, / (A) == <* — «) / (9. где или чт0 / (A + K) — / (a) = hf (a + 64A), (1) Где 0 <b1 <1. В настоящее время существуют дополнительные ограничения на f (x). Предположим, что f (x) непрерывна для <x <b и / (x) существует для <x <b. / () — / () • — (b-x) f (x) -) 5 {/ (b) — / (a) — (b-a) / (a)}. Эта функция исчезает при x = a и x = b, а ее производная ^^ {/ () — / (a) — (d-a) / (a) a) V (a)};
Следовательно, я существую между a и b. $ = a — (- (b-a), где 0 b4 1 Число = / («) + < -«) / («) + i число -e) 2 / ‘(O- Если b = a -} — Λ, получается уравнение f (a + Λ) = f (a) + hf (a) + — Λ (a + baL). (2) Это представление так называемой средней теоремы второго порядка. 126, особенно предлагаемая земля «
Следовательно, эта формула исчезает для значения x между a и b. Людмила Фирмаль
Условия f ′ (a) и f ′ (b) и это предположение, вообще говоря, f (x) для значения x вне интервала (a, b) в левой части a и правой части b Содержит описание значения. В приложении f (x) не может быть определено снаружи (a, b). В таких случаях, например, следует понимать / ‘(i) lim a £ + A> — / 0. л- + л Такое определение не зависит от внешнего (a, b) значения x. Это утверждение полностью аналогично утверждению о непрерывности в конце .
Аналогичная ситуация возникает для производных высшего порядка следующей теоремы. По аналогии с (1) и (2) мы приходим к следующей теореме. Теорема Тейлора является общей теоремой о среднем значении. / C «1) (x) непрерывен для N = / (<) + ( — «) / (a) + (от b до» y / ‘(a) + … + Где a <[E <[b, а b = a-) -ht / (A + h) = f (a) + hf \ a) + {, h * f (a) + … + W + 1njf [n] (* + M). Где 0 <0H <1. Непрерывность / (n_1) (jc) обязательно сопровождается непрерывностью / (*), f ‘(x) ….. fln ~ V (x). Доказательство проводится так же, как и в случае / 2 = 1 и n = 2. где Fn (*) = / <*> -Ax) — <* — ) / ‘() -…-
| Площади фигур, ограниченных плоскими кривыми | Ряд Тейлора |
| Длины плоских кривых | Касание плоских кривых |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Эта функция исчезает при x = a, а при x = b ее производная И между a и b должно быть значение x, которое делает это выражение исчезающим. Это сразу подразумевает описание теоремы. Другая форма теоремы Тейлора. Существует еще одна форма теоремы Тейлора, которая предполагается менее 150. Предположим, что f (x) имеет n производных f ‘(a), …, f (x) (a) и x = a. Присутствие / M (x) в любой точке означает наличие / (v-0 (x) на некотором интервале, включая эту точку, и его непрерывность в этой точке; Производная n-2 непрерывна в некотором интервале, включая точку x = a> a (n-1), — производная непрерывна в точке x = a, но если есть производная a / z в точке, отличной от x = a Не предполагает.
Во-первых, установите μ> 0, Fn (футы) —f (a + футы) — / (a) -hf (a) -…- / » » («) • Затем Fn (A) и его первая n-1 производная обращаются в нуль при h = 0 и f (>) (0) = f) (a). Так что, если мы положим G (футы) = Fn (A) — £ — {/ * «) U-8}, Где S положительно. G (0) = 0, O ‘(0) = 0, …, G (n_1) (0) = 0, 0 (n) (0) = a> 0 Два последних соотношения и теоремы §122 . Кроме того, G (n ~ 2) (0) = 0 и G (n_1) (A) ^> 0 — небольшой положительный h \, поэтому результат 122 равен 1, G (n ~ q) 0 — небольшой положительный Повторите этот аргумент (который является h1), 0 (i ~ 3) (A), 0 (n ~ 4) (A), …, и, наконец, Q (h) является положительным, т.е. ML «</ («) («) -8} H если маленький положительный.
Из A видно, что OS «1) (A) увеличивается в точке h = 0 и является положительной для небольшого положительного значения h Людмила Фирмаль
Нравится ‘) Fn <) <- £ {/ f «» (e) + 8} Для небольшого положительного A S представляет любое положительное число в этих неравенствах. В сопровождении ^ Number = {/ ‘»‘ («) + h), Где tj-v 0 справа как h- * 0. Рассматривая отрицательный случай A таким же образом, мы приходим к следующей теореме. Если f (x) имеет n производных от x = a, /, / 1—1 (1) Да + A) = / («) + hf (a) + … + (<| Д_1) tГ» 1 («) + Где tq-> 0 как h- + Q В нотации §98 вы можете написать (1) вместо (2) f (a + h) = f (a) + hf (a) + … + y ^ p / » (c) + o ( «) • Эти уравнения также могут быть получены из 150 теорем, но только в предположении непрерывности fW (x) для x = a.

