Оглавление:

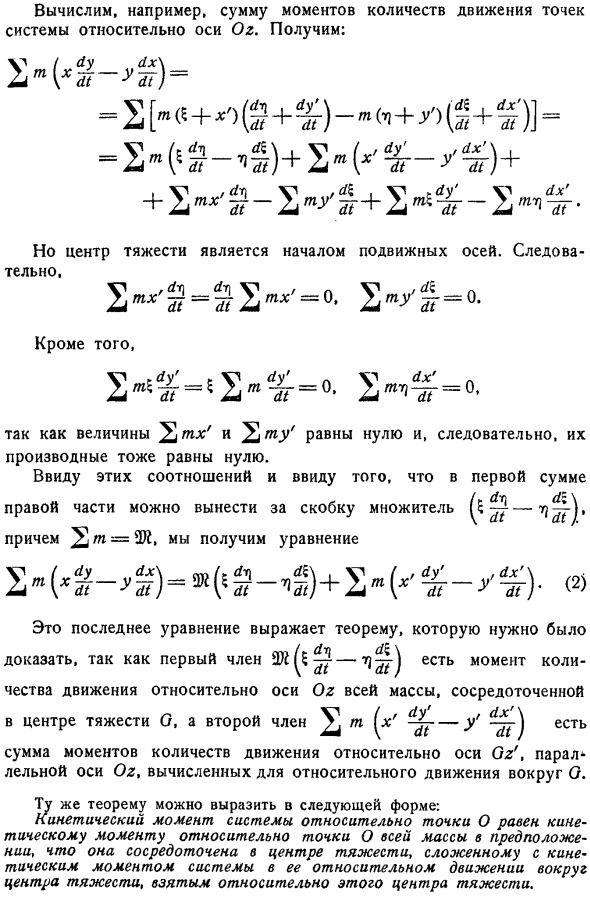
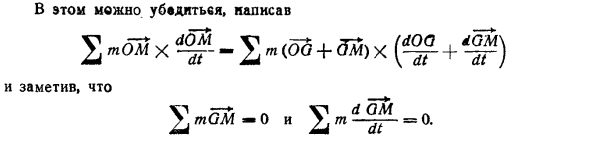

Теоремы кинематики для вычисления моментов количеств движения и кинетической энергии
- Определение относительного движения системы вокруг центра тяжести. Думаю, движущейся системы к неподвижной оси Oxyz. Пройдите через центр тяжести G этой системы и нарисуйте ось Gx y z параллельно неподвижной оси рис.193. Относительное движение системы по оси Gx y z on. Относительное движение системы вокруг центра тяжести называется. Вычисление суммы моментов импульса для фиксированной оси. Вводя это относительное движение, мы можем сформулировать следующую теорему: теорема.
Эта последняя кривая, обязательно составленная из дуг, дающих каждая в отдельности относительный минимум, состоит, следовательно, из дуг траекторий. Людмила Фирмаль
Импульс движения относительно неподвижной оси считается равным и сосредоточенным на импульсе всей массы системы В центроиде она увеличивается на сумму моментов импульса относительно оси через центроид и проходит через центроид. Центр тяжести вычисляется относительно относительного движения вокруг центра тяжести. Доказательство исходит непосредственно из основной формулы преобразования координатных осей. x, y, z координаты некоторой точки системы относительно неподвижной оси, x , y , z координаты той же точки относительно координатных осей Gx , Gy , Gz , проведенных через центр тяжести параллельно неподвижной оси, а через 5 C координаты центроида.
- Тогда, согласно формуле преобразования оси, существуют: 1 например, вычислите сумму моментов импульсных точек системы относительно оси Oz. Что взять = 2 т о + т у + + 2 2 J E I7 Но центр тяжести это только начало. См = = 0 Ось работает. Резьбовой стержень Также поскольку величины tx и tu равны нулю, их производные также равны нулю.
Принимая во внимание эти соотношения и тот факт, что фактор можно заключить в скобки с первой суммой справа, получим уравнение Это последнее уравнение представляет собой теорему, которую необходимо доказать с первого члена Есть такие моменты Движение относительно центроида G, 2 й сумма моментов движения относительно оси GZ, параллельной оси Oz и относительно оси G. Ось Oz всей массы сконцентрирована 2 Члены Вот оно.
Это следует из того, что для нахождения таких кривых нужно прежде всего приравнять нулю вариацию действия. Людмила Фирмаль
Ту же теорему можно выразить в следующем виде: Момент движения системы относительно точки о равен моменту движения относительно точки о всей массы в предположении, что она сосредоточена в центре тяжести, и совмещается с моментом движения системы относительно этого центра тяжести.
Смотрите также:
Решение задач по теоретической механике
| Размерности | Вычисление кинетической энергии |
| Важный частный случай, когда работа реакций связей равна нулю | Теорема моментов количеств движения в относительном движении вокруг центра тяжести |

