Оглавление:
Теорема Виета. Обратная теорема. Теорема об определении знаков корней квадратного уравнения по его коэффициентам
Свойства корней квадратного уравнения, их связь с коэффициентами уравнения, о которых пойдёт речь в этом пункте, впервые были установлены французским математиком Франсуа Виетом (1540-1603).
Теорема (Виета). Пусть дано квадратное уравнение
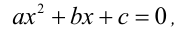
у которого дискриминант неотрицателен 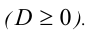 Тогда корни
Тогда корни  ,
, 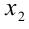 , и коэффициенты а,b,c этого уравнения связаны между собой системой соотношений:
, и коэффициенты а,b,c этого уравнения связаны между собой системой соотношений:
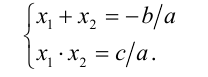
Доказательство. Пусть  ,
,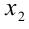 — корни уравнения.
— корни уравнения.
1) Рассмотрим сумму корней 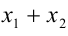 . Согласно формуле корней квадратного уравнения имеем
. Согласно формуле корней квадратного уравнения имеем
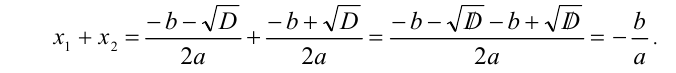
2) Аналогично для произведения корней получим
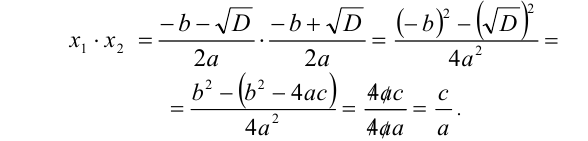
Замечание. Формулы для суммы и произведения корней квадратного уравнения остаются верными и в случае, когда уравнение имеет единственный корень  . В этом случае следует положить в указанных формулах
. В этом случае следует положить в указанных формулах 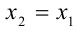 .
.
Пример №157.
При каком значении k корни уравнения 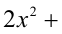
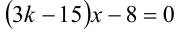 будут противоположными числами?
будут противоположными числами?
Решение:
Воспользуемся для решения задачи теоремой Виета. Во-первых, для того чтобы уравнение имело корни, необходимо и достаточно, чтобы его дискриминант был неотрицателен. Во-вторых, условие противоположности корней можно записать в виде 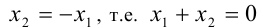 . По теореме Виета сумма корней уравнения равна
. По теореме Виета сумма корней уравнения равна 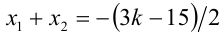 . Тогда задача сводится к решению системы
. Тогда задача сводится к решению системы
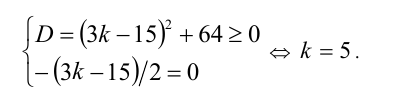
Обратная теорема к теореме Виета формулируется для приведённого уравнения. Это объясняется тем, что, зная два корня, невозможно однозначно определить все три коэффициента уравнения, поэтому для определённости полагают старший коэффициент 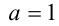 .
.
Теорема (обратная теореме Виета). Если данные действительные числа  и
и 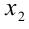 таковы, что
таковы, что
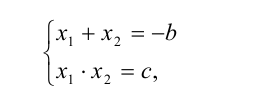
то  и
и 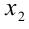 являются корнями приведённого квадратного уравнения
являются корнями приведённого квадратного уравнения
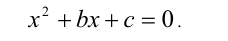
Доказательство. Так как по условию
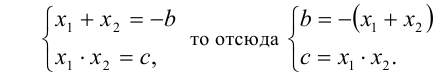
Подставим в квадратный трёхчлен 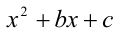 вместо коэффициентов b и c полученные выражения:
вместо коэффициентов b и c полученные выражения:
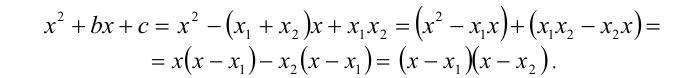
Уравнение 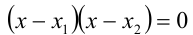 — очевидно, имеет корни
— очевидно, имеет корни  и
и 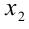 (и никаких других). Следовательно, равносильное ему уравнение
(и никаких других). Следовательно, равносильное ему уравнение 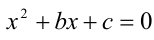 также имеет эти корни.
также имеет эти корни.
Из теоремы Виета и обратной к ней теоремы вытекает следующая теорема, позволяющая без решения квадратного уравнения (т.е. без нахождения в явном виде корней  и
и 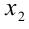 ), пользуясь только знанием коэффициентов а,b,c , определить знаки его корней. Сформулируем эти необходимые и достаточные условия.
), пользуясь только знанием коэффициентов а,b,c , определить знаки его корней. Сформулируем эти необходимые и достаточные условия.
Теорема (об определении знаков корней квадратного уравнения по известным коэффициентам). Пусть квадратное уравнение 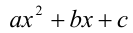 имеет действительные корни. Тогда справедливы следующие утверждения:
имеет действительные корни. Тогда справедливы следующие утверждения:
1) уравнение имеет два положительных корня 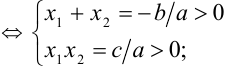
2) уравнение имеет два отрицательных корня 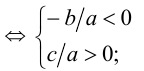
3) уравнение имеет корни разных знаков 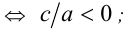
4) уравнение имеет положительный и нулевой корни 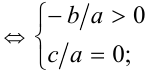
5) уравнение имеет отрицательный и нулевой корни 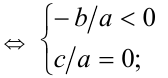
6) уравнение имеет два нулевых корня 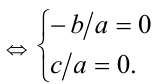
Приведённая теорема играет важную роль при решении задач, связанных с исследованием расположения корней квадратного уравнения относительно точки x = 0, т.е. связанных с исследованием их знаков.
Пример №158.
Найти, при каких значениях параметра m уравнение 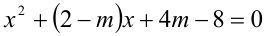 имеет два различных действительных корня и они оба положительны.
имеет два различных действительных корня и они оба положительны.
Решение:
Во-первых, чтобы действительные корни существовали и были различны, необходимо и достаточно выполнения условия D > 0 . Во-вторых, для учёта положительности корней воспользуемся последней из теорем. Таким образом, искомые значения параметра ищем как решения системы
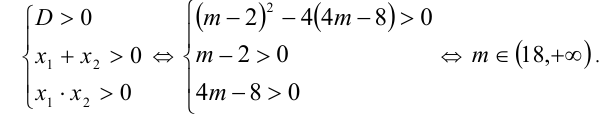
Пример №159.
Известно, что квадратное уравнение
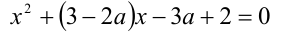
имеет корни. Не решая уравнения, определить знаки его корней.
Решение:
Воспользуемся последней из сформулированных теорем. 1) Выясним, например, при каких значениях параметра данное приведённое уравнение имеет корни разных знаков. Для этого необходимо и достаточно, чтобы свободный член 2 — 3а < 0, т.е. при а > 2/3 .
2) Выясним теперь, при каких значениях параметра оба корня отрицательны. Нахождение таких а сводится к решению системы
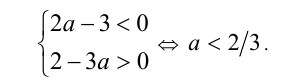
3) Осталось исследовать значение а = 2/3 . При этом значении параметра обнаруживаем, что сумма корней, равная 2а — 3 , отрицательна, а произведение корней, равное 2 — 3а , равно нулю. Поэтому в силу той же теоремы делаем вывод: один корень отрицателен, другой равен нулю.
Кроме того, при решении задач, связанных с теоремой Виета, могут оказаться полезными следующие соотношения [24], выражающие некоторые распространенные комбинации чисел  , и
, и 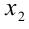 , через их сумму и произведение:
, через их сумму и произведение:
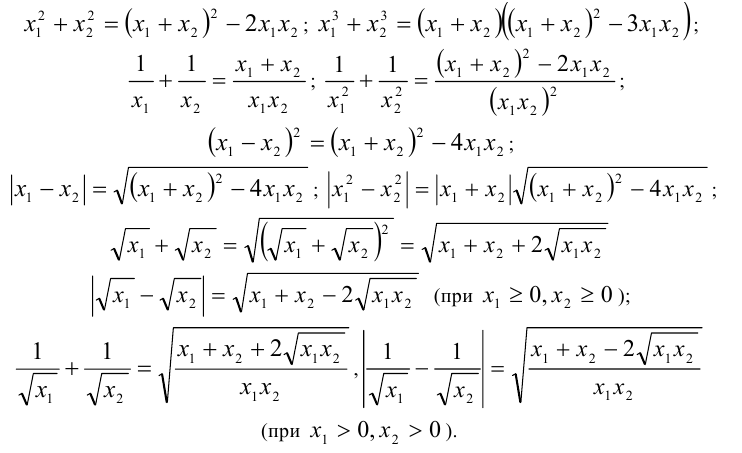
Такого рода преобразования используются при решении квадратных уравнений, коэффициенты которых содержат параметр, а постановка задачи имеет форму: «не решая уравнения, найти 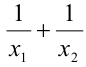 », «при каких значениях параметра уравнение имеет действительные корни с заданной суммой квадратов», «при каких значениях параметра уравнение имеет действительные корни, произведение которых меньше заданного числа» и т.п.
», «при каких значениях параметра уравнение имеет действительные корни с заданной суммой квадратов», «при каких значениях параметра уравнение имеет действительные корни, произведение которых меньше заданного числа» и т.п.
Пример №160.
Пусть (х;у) — решение системы уравнений
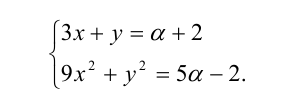
При каком значении 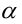 произведение ху принимает наибольшее значение?
произведение ху принимает наибольшее значение?
Решение:
Поскольку 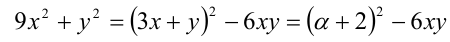 , то система равносильна системе
, то система равносильна системе
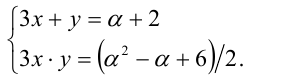
Согласно обратной теореме Виета, числа Зх и у являются корнями квадратного уравнения
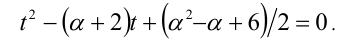
Для их существования необходимо и достаточно выполнения условия неотрицательности дискриминанта:
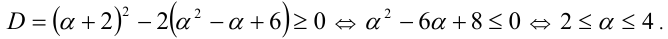
Задача свелась к нахождению наибольшего значения
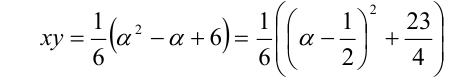
как квадратичной функции 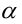 на отрезке [2,4]. Поскольку на этом отрезке данная функция монотонно возрастает, то она принимает своё наибольшее значение на его правом конце, т.е. при
на отрезке [2,4]. Поскольку на этом отрезке данная функция монотонно возрастает, то она принимает своё наибольшее значение на его правом конце, т.е. при 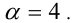
Итак, 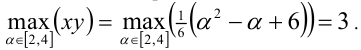
Пример №161.
Дано:  , и
, и 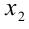 — корни квадратного уравнения
— корни квадратного уравнения 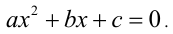 Составить алгебраическое уравнение наименьшей степени, корни которого
Составить алгебраическое уравнение наименьшей степени, корни которого 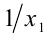 и
и 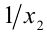
Решение:
Требуемое уравнение будем искать в виде
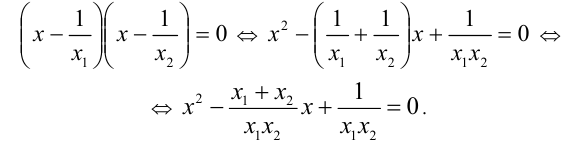
Учитывая, что согласно теореме Виета для исходного уравнения
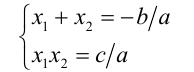
(по условию 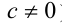 ), окончательно получаем:
), окончательно получаем:
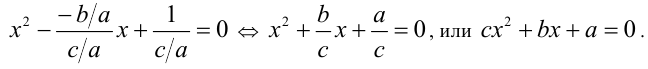
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

