Оглавление:




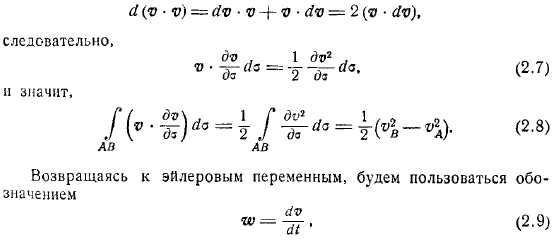

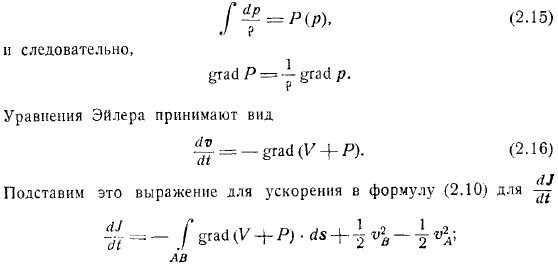


Теорема Томсона
В году Гельмгольц установил дифференциальное уравнение для вектора вихря в своих знаменитых мемуарах, из которых он вывел основную теорему гидромеханики о сохранении прочности вихрей и труб. Тогда теорема Гельмгольца называется. Это показал Томсон по-другому. Метод Томсона основан на распространении концепции скоростной циркуляции. Понятие скоростной циркуляции является известным понятием, тесно связанным с понятием скоростного вихря.
Изучение вихревого движения начинается с предложения метода Томсона. Рассмотрим несколько линий, нарисованных на жидкости. Рассмотрим эту линию как линию жидкости, то есть линию, состоящую из жидкости. В другие основные уравнения теории вихрей и теоремы Гельмгольца о сохранении вихрей и моменты времени частицы, составляющие линию, образуют новую линию. Теперь рассмотрим линейный интеграл скорости вдоль линии, то есть формулу. Если линия замкнута, интеграл превращается в циркуляцию скорости по замкнутому контуру.
В момент частицы жидкости образуют линию, линейный интеграл на равен значению, а — вектору скорости в момент времени. Создайте производную времени для характеристики изменения во времени. То есть мы создаем следующее выражение. Первая задача — рассчитать сумму. Рассмотрим частицы жидкости в. Момент кривой.
Каждая такая частица характеризуется значением параметра. Например, этим параметром может быть длина дуги кривой, которая отсчитывается от точки. Ясно, что декартовы координаты частиц жидкости в момент времени на кривой будут функцией как от, так и от. Другими словами, радиус-вектор точки относительно начала координат является функцией.
Теоремы Томсона и Тета ― формулируют условия, необходимые для того, чтобы можно было стабилизировать гироскопическими силами неустойчивую потенциальную систему. Были доказаны в 1879 г. Людмила Фирмаль
Циклическое выражение описывается следующим образом: является независимой переменной формулы, поэтому при дифференцировании на следует считать константой. Далее, по определению скорости, следовательно — ускорение частицы. Таким образом, для первого члена справа уравнение строится точно так же, как и линейный интеграл ускорения для члена существует очевидное выражение, аналогично.
Следовательно, означает. Формула принимает вид. Это желательные отношения. Если контур представляет собой замкнутую линию, то точки совпадают, а поэтому формула теоремы Лагранжа упрощается и принимает вид. Выполняется следующая теорема: теорема состоит в том, что производная по времени циркуляции скорости вдоль замкнутого контура равна циркуляции ускорения вдоль того же контура. Теперь, используя основное уравнение движения для идеальной жидкости в форме Эйлера, мы делаем следующие предположения: сила, действующая на единицу массы жидкости, имеет потенциал, поэтому.
Давление жидкости вперед, то есть рассмотреть. В этом случае, следовательно,.уравнение Эйлера принимает вид. Подставьте это уравнение ускорения в уравнение; однако по самому определению, выражение держится. Другими словами. Для замкнутого контура точки совпадают, а уравнение принимает вид, и после интегрирования сразу получаем. Это равенство является основной теоремой Томсона. Теорема Томсона: если массовая сила принимает потенциал, а идеальная жидкость является баротропной, то циркуляция скорости по замкнутому контуру во всем движении жидкости не изменяется.
Пользуясь теоремой Томсона и Тета, можно исследовать устойчивость волчка, системы инерциальной навигации и гироскопического однорельсового вагона. Людмила Фирмаль

