Теорема об изменении момента количества движения точки в теоретической механике

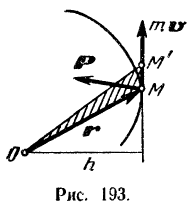
Теорема об изменении момента количества движения точки

Пусть материальная точка 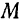Теорема об изменении момента количества движения точки массы 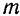движется под действием приложенной к ней силы 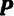(рис. 193).

Момент количества движения данной точки относительно какого-либо неподвижного центра 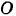Теорема об изменении момента количества движения точки согласно формуле (168)

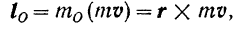
где 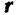Теорема об изменении момента количества движения точки — радиус-вектор, соединяющий центр 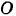с точкой .

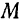Так как в общем случае движения точки векторы 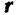и 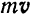являются переменными векторами, то, по правилу нахождения производной произведения двух функций, будем иметь:

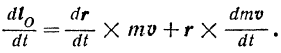
Но

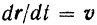
и, следовательно

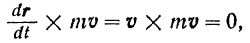
так как угол

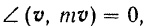
и потому модуль векторного произведения

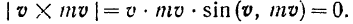
По теореме о количестве движения материальной точки (формула (157)):

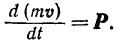
Подставляя найденные значения в правую часть равенства (I), получаем:

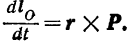
Векторное же произведение радиуса-вектора 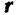Теорема об изменении момента количества движения точки точки 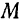приложения силы на силу 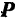есть момент 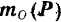этой силы относительно центра .

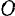Таким образом, окончательно получаем:

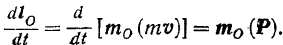
Производная по времени от момента 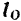Теорема об изменении момента количества движения точки количества движения 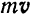материальной точки относительно какого-либо центра равна моменту силы 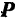, действующей на точку, относительно того же центра.

Проектируя векторное равенство (171) на какую-нибудь неподвижную ось 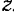Теорема об изменении момента количества движения точки , проходящую через центр 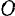момента, будем иметь:

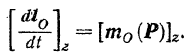
Но проекция производной вектора на неподвижную ось равна производной от проекции этого вектора на эту ось.

На оснований этого и учитывая зависимость (169), получаем

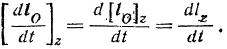
Согласно же известной из статики зависимости (33):

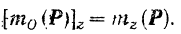
Подставляя значения (III) н (IV) в равенство (II), окончательно получаем:

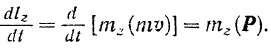
Производная по времени от момента 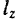Теорема об изменении момента количества движения точки количества движения точки относительно какой-либо неподвижной оси 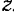равна моменту силы 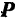, действующей на точку, относительно той же оси.

Из уравнения (172) вытекает следствие:

Если момент 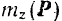Теорема об изменении момента количества движения точки силы, действующей на точку, относительно какой-либо оси в течение некоторого времени равен нулю, то момент количества движения данной точки относительно этой оси все это время остается постоянным.

Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:

Теоретическая механика — задачи с решением и примерами

Возможно вам будут полезны эти дополнительные темы:

Закон сохранения количества движения системы

Теорема о движении центра масс системы с примерами решения

Движение материальной точки под действием центральной силы

Кинетический момент системы относительно центра и относительно оси с примером решения