Теорема об изменении количества движения системы
Разделим все силы, действующие на систему, на внешние и внутренние. Равнодействующую внешних сил, действующих на какую-либо 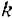 -ю точку системы, обозначим через
-ю точку системы, обозначим через 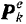 и равнодействующую внутренних сил — через
и равнодействующую внутренних сил — через 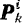 . Тогда, на основании теоремы об изменении количества движения материальной точки, можно написать следующее равенство:
. Тогда, на основании теоремы об изменении количества движения материальной точки, можно написать следующее равенство:
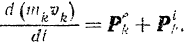
Составляя аналогичные уравнения для всех точек системы и суммируя их почленно, получим:
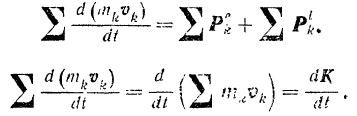
Геометрическая же сумма всех внутренних сил системы
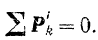
Учитывая равенства (II) и (III), уравнение (I) можно записать следующим образом:
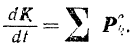
Производная по времени от, количества движения системы равна главному вектору всех внешних сил, действующих на систему.
Так как проекция производной от вектора на какую-либо ось равна производной от проекции вектора на ту же ось, то векторное уравнение (160) эквивалентно трем скалярным уравнениям
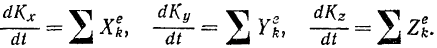
Производная по времени от проекции количества движения системы на какую-либо ось равна сумме проекций на ту же ось всех внешних сил, действующих на систему.
Иногда бывает удобней пользоваться теоремой об изменении проекции количества движения системы в конечной форме.
Умножив обе части уравнений (161) на 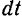 и интегрируя их в соответствующих пределах, будем иметь:
и интегрируя их в соответствующих пределах, будем иметь:
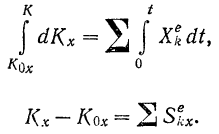
Изменение проекции количества движения системы на какую-либо ось за некоторый промежуток времени равно сумме проекций на ту же ось импульсов всех внешних сил, действующих на систему, за тот же промежуток времени.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
| Импульс силы |
| Теорема об изменении количества движения материальной точки с примерами решения |
| Закон сохранения количества движения системы |
| Теорема о движении центра масс системы с примерами решения |

