Оглавление:
Теорема об изменении количества движения материальной точки
Как известно из кинематики (§ 45), ускорение 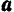 точки равно производной от ее скорости
точки равно производной от ее скорости 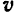 по времени:
по времени:
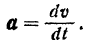
Подставляя это значение 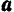 в основное уравнение (106) динамики точки, будем иметь:
в основное уравнение (106) динамики точки, будем иметь:
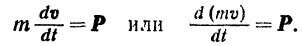
Производная по времени от количества движения материальной точки равна силе, действующей на точку (теорема об изменении количества движения точки в дифференциальной форме).
Разделяя переменные в уравнении (157) и интегрируя обе части его в соответствующих пределах, будем иметь:
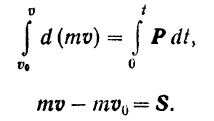
Изменение количества движения материальной точки за некоторый промежуток времени равно импульсу силы, действующей на точку за то же время (теорема об изменении количества движения точки в конечной векторной форме).
Если известны масса 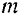 точки и ее скорость
точки и ее скорость 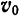 и
и 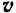 в начальный и в данный моменты времени, то, пользуясь равенством (158), легко построить импульс
в начальный и в данный моменты времени, то, пользуясь равенством (158), легко построить импульс 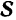 силы, действующей на точку за соответствующий промежуток времени (рис. 184). Наоборот, если известен импульс
силы, действующей на точку за соответствующий промежуток времени (рис. 184). Наоборот, если известен импульс 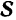 и начальная скорость
и начальная скорость 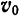 , то можно найти скорость
, то можно найти скорость 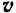 точки в данный момент.
точки в данный момент.
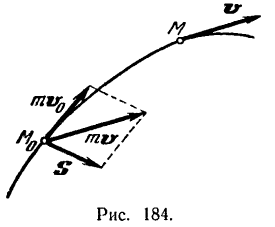
Однако при решении задач обычно удобней пользоваться уравнением (158) не в векторной форме, а в координатной форме.
Проектируя обе части равенства (158) на координатные оси, будем иметь:
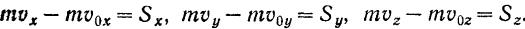
Изменение проекции количества движения материальной точки на какую-либо ось за некоторый промежуток времени равно проекции на ту же ось импульса силы, действующей на точку, за тот же промежуток времени (теорема об изменении проекции количества движения точки).
В случае прямолинейного движения точки теорема выражается одним из уравнений (159), если прямую, по которой движется точка, принять за соответствующую координатную ось.
«С помощью теоремы об изменении количества движения точки легко решаются задачи, в которых на точку (или на тело, движущееся поступательно) действуют постоянные силы или силы, зависящие только от времени, и когда в число заданных и искомых величин, помимо сил, действующих на точку, входят время движения и скорости точки в начале и в конце данного промежутка времени.
Пример задачи:
Тело весом 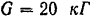 движется поступательно вверх по негладкой плоскости, наклоненной к горизонту под углом
движется поступательно вверх по негладкой плоскости, наклоненной к горизонту под углом 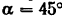 , под действием силы
, под действием силы 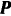 , составляющей с плоскостью угол
, составляющей с плоскостью угол 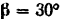 (рис. 185). Чему должен равняться модуль силы
(рис. 185). Чему должен равняться модуль силы 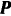 , для того чтобы через 10 сек после начала движения тело получило скорость
, для того чтобы через 10 сек после начала движения тело получило скорость 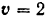 м/сек? Коэффициент трения
м/сек? Коэффициент трения 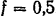 .
.
Решение:
Поступательно движущееся тело принимаем за материальную точку 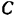 , полагая, что в ней сосредоточена вся масса тела. На нее действуют силы:
, полагая, что в ней сосредоточена вся масса тела. На нее действуют силы: 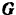 — сила тяжести тела, сила
— сила тяжести тела, сила 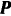 , нормальная реакция
, нормальная реакция 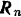 плоскости и сила
плоскости и сила 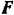 трения.
трения.
Прямую, по которой движется точка 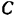 , принимаем за ось
, принимаем за ось 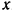 . Согласно теореме об изменении проекции количества движения точки:
. Согласно теореме об изменении проекции количества движения точки:
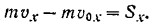
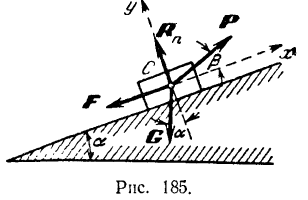
Так как силы, действующие на точку, постоянны, то
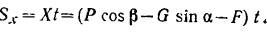
Для определения нормальной реакции плоскости спроектируем все силы на ось 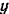 :
:
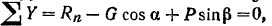
откуда
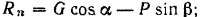
модуль силы трения
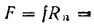
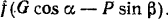
По условиям задачи
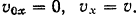
Подставляя найденные значения в уравнение (I), будем иметь:
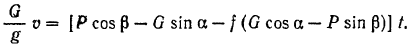
Решая это уравнение относительно 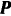 , находим:
, находим:
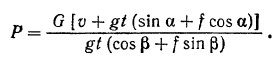
Подставляя данные, получим:
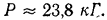
Пример задачи:
Молот весом 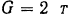 падает с высоты
падает с высоты 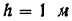 на поковочную болванку; деформация болванки происходит в течение
на поковочную болванку; деформация болванки происходит в течение 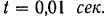 . Определить среднюю величину силы давления молота на болванку.
. Определить среднюю величину силы давления молота на болванку.
Решение:
На молот действуют вертикальные силы: сила 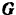 тяжести и реакция болванки. Переменную, изменяющуюся в течение данного промежутка времени
тяжести и реакция болванки. Переменную, изменяющуюся в течение данного промежутка времени 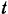 величину реакции болванки заменим некоторым ее средним значением
величину реакции болванки заменим некоторым ее средним значением 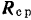 .
.
Примем направление движения молота (вертикально вниз) за направление оси 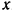 и применим теорему об изменении количества движения к движению молота за промежуток времени от момента его соприкосновения с болванкой до момента, когда заканчивается ее деформация и скорость молота обращается в нуль. По формуле (159)
и применим теорему об изменении количества движения к движению молота за промежуток времени от момента его соприкосновения с болванкой до момента, когда заканчивается ее деформация и скорость молота обращается в нуль. По формуле (159)
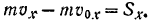
В данном уравнении конечная скорость 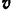 молота и ее проекция
молота и ее проекция 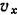 равны нулю. Начальная скорость молота по известной из физики формуле
равны нулю. Начальная скорость молота по известной из физики формуле 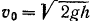 и направлена вертикально вниз.
и направлена вертикально вниз.
Проекция на ось 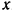 равнодействующей всех сил, действующих на молот,
равнодействующей всех сил, действующих на молот,
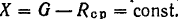
Следовательно,
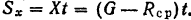
Подставляя эти значения в уравнение, получим:
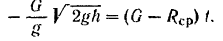
Отсюда реакция болванки, равная по модулю искомому давлению молота, будет равна
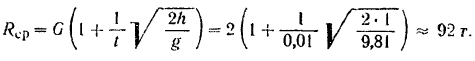
Пример задачи:
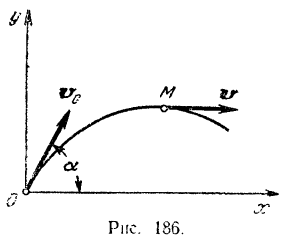
Найти импульс равнодействующей всех сил, действующих на снаряд за время, когда он из начального положения 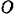 переходит в наивысшее положение
переходит в наивысшее положение 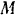 (рис. 186). Дано:
(рис. 186). Дано: 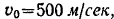
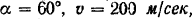 вес снаряда
вес снаряда 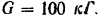
Решение:
Пренебрегая вращательным движением снаряда, принимаем его за материальную точку.
По теореме об изменении проекции количества движения точки находим проекции на координатные оси импульса действующих па нее сил:
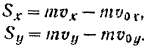
В данном случае:
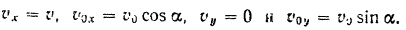
Следовательно
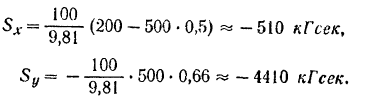
Модуль импульса
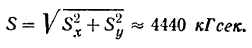
Направляющие косинусы

Отсюда углы между вектором 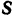 и осями координат:
и осями координат:
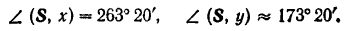
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
| Выражение количества движения системы через массу системы и скорость ее центра масс |
| Импульс силы |
| Теорема об изменении количества движения системы |
| Закон сохранения количества движения системы |

