Теорема об изменении количества движения
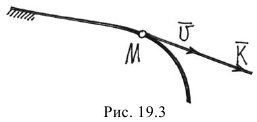
Количеством движения материальной точки называется произведение массы точки на ее скорость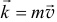 
. Это есть вектор, который направляется как вектор скорости по касательной к траектории (рис. 19.3).
Количеством движения материальной системы будем называть векторную сумму количеств движения всех точек системы
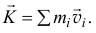
Как известно (14.1), радиус-вектор центра масс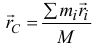 
или 
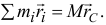Найдем производную по времени от этого равенства 
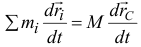или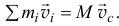 
Значит по формуле (19.3) количество движения материальной системы при любом ее движении определяется довольно просто как произведение массы системы на скорость ее центра масс
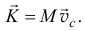
Направляется вектор количества движения так же, как вектор скорости центра масс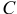 
. Количество движения точки — связанный вектор, он приложен к этой точке. Поэтому и для вектора количества движения системы можно ввести понятие точки приложения. Правда, найти ее не всегда просто. Но при поступательном движении твердого тела это сделать несложно.
Так как при поступательном движении все точки тела имеют равные, параллельные векторы скорости, то и векторы количества движения их будут параллельны. Поэтому точку приложения вектора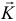 
можно определять как центр параллельных векторов 
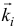(см. раздел «Статика»), радиус-вектор которого
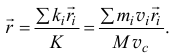
Но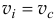 
значит 
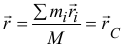, равен радиусу-вектору центра масс, то есть вектор количества движения тела при поступательном движении приложен к центру масс. При других движениях тела определить точку приложения вектора 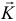сложнее.
Введем еще одно понятие — импульс силы. Импульсом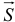 
постоянной силы 
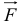за время ее действия 
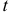называется произведение
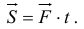
Если же сила переменна, то определяют сначала элементарный импульс за время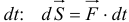 
, а потом интегрируют на интервале от t
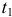до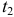 
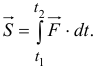
Перейдем теперь к выводу теоремы.
Запишем для каждой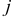 
-й точки материальной системы основное уравнение динамики, разделив силы на внешние и внутренние:
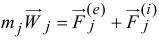
или
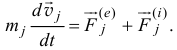
Введем массу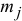 
под знак дифференциала
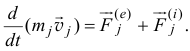
Сложим эти равенства. Получим
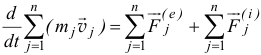
или
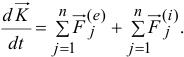
Но последняя сумма, векторная сумма внутренних сил, равна нулю. Поэтому
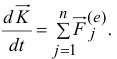
Производная по времени от вектора количества движения материальной системы равна векторной сумме внешних сил, приложенных к точкам системы.
Чтобы получить уравнения, удобные для исследования движения системы, спроектируем векторное равенство (19.7) на оси:
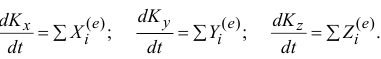
И ещё. Проинтегрируем уравнение (19.7) за время перехода системы из какого-нибудь одного положения в другое
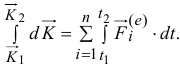
Получим теорему об изменении количества движения, записанную в другой форме:
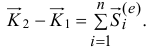
Изменение количества движения материальной системы при переходе ее из одного положения в другое равно векторной сумме импульсов внешних сил за время перехода.
Спроектировав векторное равенство (19.9) на оси, получим скалярные уравнения, которые используются при решении задач:
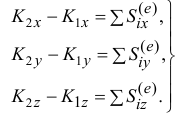
Разность проекций вектора количества движения в конечном и начальном положениях системы на ось равна сумме проекций импульсов внешних сил на эту ось.
Теорему об изменении количества движения обычно используют для решения задач, по условию которых требуется установить зависимость между изменениями массы, перемещением тел системы и их скорости.
Эта теория взята со страницы помощи с решением заданий по теоретической механики, там найдёте другие лекции и примеры решения задач или сможете заказать онлайн помощь:
Помощь по теоретической механике
Кстати возможно вам будут полезны эти страницы:
| Обобщенные силы инерции в теоретической механике |
| Теорема о движении центра масс |
| Теорема об изменении момента количества движения |
| Дифференциальные уравнения вращения твердого тела |
