Оглавление:
Теорема об изменении кинетической энергии точки
Пусть материальная точка 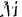 массы
массы 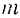 под действием приложенной к ней силы
под действием приложенной к ней силы 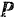 движется по некоторой траектории, перемещаясь из наложения
движется по некоторой траектории, перемещаясь из наложения 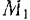 в положение
в положение 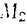 (рис. 210).
(рис. 210).
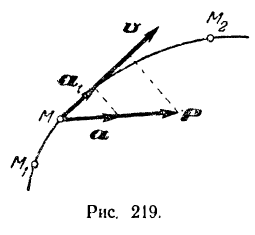
Согласно основному уравнению (106) динамики точки 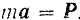 Спроектировав обе части этого векторного уравнения на направление скорости
Спроектировав обе части этого векторного уравнения на направление скорости 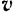 точки
точки 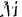 умножив их на одни и тот же скалярный множитель
умножив их на одни и тот же скалярный множитель 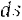 (элементарное перемещение точки), будем иметь:
(элементарное перемещение точки), будем иметь:
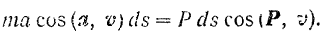
Но как известно из кинематики,
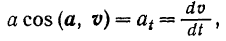
правая же часть равенства (I) представляет собой выражение элементарной работы силы:
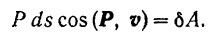
Подставляя значения (II) и (III) в равенство (I), получим:
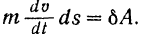
Так как
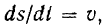
мы приходим к равенству
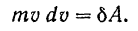
Интегрируя обе части последнего равенства в соответствующих пределах и обозначая через 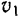 модуль скорости в начальный момент, когда точка занимает на траектории положение
модуль скорости в начальный момент, когда точка занимает на траектории положение 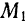 , и через
, и через 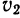 — модуль скорости точки в момент, когда она занимает положение
— модуль скорости точки в момент, когда она занимает положение 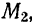 , находим:
, находим:
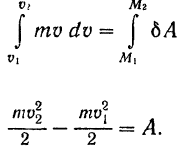
Скалярная величина 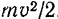 , равная половине произведения массы точки на квадрат ее скорости, называется кинетической энергией точки.
, равная половине произведения массы точки на квадрат ее скорости, называется кинетической энергией точки.
Следовательно, уравнение (205), выражающее собой теорему об изменении кинетической энергии точки, можно сформулировать так:
Изменение кинетической энергии точки на некотором ее перемещении равно работе силы, действующей на точку, на том же перемещении.
Если движение материальной точки совершалось под действием не одной, а нескольких приложенных к ней сил, то под работой в уравнении (205) надо понимать работу равнодействующей этих сил.
Размерность кинетической энергии
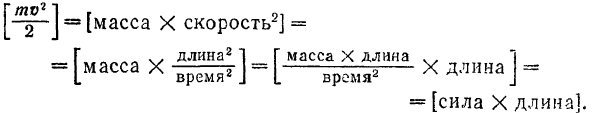
Таким образом, кинетическая энергия имеет ту же размерность, что и работа.
Если под действием сил сопротивления, приложенных к данной материальной точке, точка останавливается, то конечная ее скорость 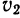 равна нулю и.уравнение (205) принимает вид:
равна нулю и.уравнение (205) принимает вид:
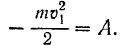
Работа сил сопротивления всегда отрицательна, поэтому отрицательной будет и правая часть написанного выше равенства.
Теорема о кинетической энергии точки позволяет определить работу приложенных к ней сил при переходе точки из одного положения в другое и в тех случаях (переменной силы и криволинейного движения точки), когда непосредственное вычисление работы является затруднительным. Для этого надо только знать массу точки и модули ее скорости в начальном и конечном положении.
Если же, наоборот, мы имеем возможность непосредственного определения работы приложенных к точке сил, то, зная массу точки и модуль ее скорости в одном положении, легко найти, пользуясь данной теоремой, модуль скорости точки в другом положении.
Теорема о кинетической энергии точки дает наиболее простой способ решения тех задач, в которых устанавливается зависимость между действующей на точку силой, скоростью точки и пройденным ею путем.
Пример задачи:
Материальная точка массы 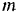 , привязанная нитью длиной
, привязанная нитью длиной 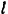 к неподвижной точке
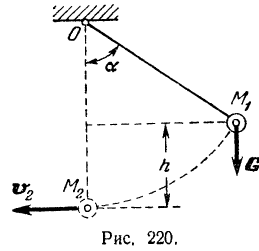
к неподвижной точке 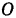 (рис. 220), отведена на угол
(рис. 220), отведена на угол 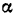 от положения равновесия
от положения равновесия 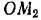 и отпущена в точке
и отпущена в точке 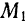 без начальной скорости. Определить скорость
без начальной скорости. Определить скорость 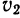 этой точки во время ее прохождения через положение равновесия.
этой точки во время ее прохождения через положение равновесия.
Решение:
По теореме об изменении кинетической энергии материальной точки
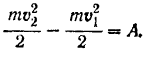
Перемещение точки из положения 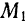 в положение
в положение 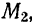 совершается под действием силы тяжести. Работа этой силы по формуле (195) равна:
совершается под действием силы тяжести. Работа этой силы по формуле (195) равна:
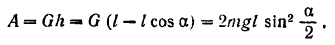
Начальная скорость точки
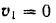
и уравнение кинетической энергии принимает вид
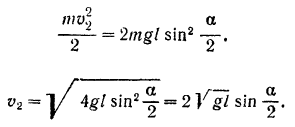
Пример задачи:
Автомобиль движется со скоростью 54 км/час под уклон, угол которого 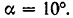 Считая силу
Считая силу 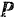 сопротивления от торможения равной 0,3 веса автомобиля и пренебрегая всеми другими сопротивлениями его движению,
сопротивления от торможения равной 0,3 веса автомобиля и пренебрегая всеми другими сопротивлениями его движению,
определить, на каком расстоянии 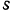 и через сколько времени
и через сколько времени 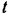 от начала торможения автомобиль остановится.
от начала торможения автомобиль остановится.
Решение:
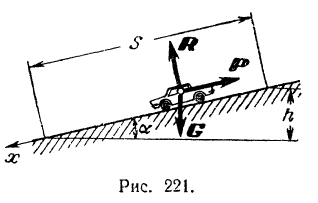
Автомобиль рассматриваем как материальную точку, на которую действуют (рис. 221) следующие силы: 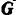 —сила тяжести автомобиля,
—сила тяжести автомобиля, 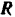 — нормальная реакция дороги и
— нормальная реакция дороги и 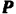 — сопротивление от торможения.
— сопротивление от торможения.
Для определения тормозного пути 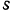 применяем теорему об изменении кинетической энергии точки:
применяем теорему об изменении кинетической энергии точки:
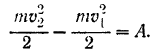
Нам известны: начальная скорость автомобиля 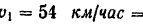
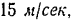 , его конечная скорость
, его конечная скорость 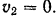
Работа 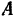 равнодействующей сил, приложенных к автомобилю, равна алгебраической сумме работ составляющих сил. Работа силы тяжести равна
равнодействующей сил, приложенных к автомобилю, равна алгебраической сумме работ составляющих сил. Работа силы тяжести равна
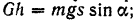
работа нормальной реакции 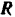 равна нулю, так как эта сила перпендикулярна к направлению движения автомобиля; работа силы
равна нулю, так как эта сила перпендикулярна к направлению движения автомобиля; работа силы 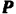 торможения отрицательна, так как эта сила направлена в сторону, противоположную направлению движения автомобиля, и равна
торможения отрицательна, так как эта сила направлена в сторону, противоположную направлению движения автомобиля, и равна
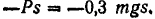
Таким образом, работа равнодействующей
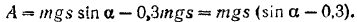
Для данного случая уравнение изменения кинетической энергии принимает вид
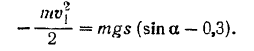
Отсюда
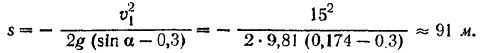
Для определения времени 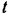 торможения можно воспользоваться теоремой об изменении проекции количества движения точки. Приняв направление движения за направление оси
торможения можно воспользоваться теоремой об изменении проекции количества движения точки. Приняв направление движения за направление оси 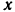 (рис. 221), напишем уравнение (159):
(рис. 221), напишем уравнение (159):
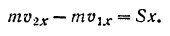
По условиям задачи
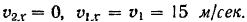
Так как действующие на автомобиль силы постоянны, то проекция на ось 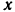 импульса этих сил
импульса этих сил
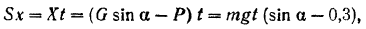
Таким образом, уравнение (159) принимает вид
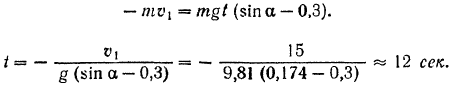
Теорема об изменении кинетической энергии системы
Применим установленную в предыдущем параграфе теорему об изменении кинетической энергии материальной точки к системе таких точек.
Согласно уравнению (205) для 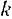 -й точки системы будем иметь:
-й точки системы будем иметь:
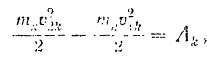
где 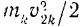 и
и 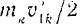 — значения кинетической энергии
— значения кинетической энергии 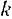 -й точки соответственно в конце и в начале некоторого перемещения системы;
-й точки соответственно в конце и в начале некоторого перемещения системы; 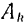 — работа на том же перемещении равнодействующей всех сил, действующих на данную точку.
— работа на том же перемещении равнодействующей всех сил, действующих на данную точку.
Написав подобные равенства для всех точек системы и сложив их почленно, получаем:
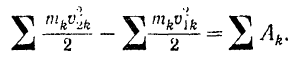
Сумма кинетических материальных точек называется энергией системы

Равно нулю только, как доказано п § 105. рабою внутренних сил неизменяемой системы.
Теоремой об изменении кинетической энергии системы хдобно пользоваться в тех случаях, когда в число данных и искомых величин задачи входят: действующие на систему силы, перемещения (линейные и угловые) тел. «ходящих в состав системы, и скорости этих тел (также линейные или угловые).
С помощью этой теоремы можно находим, также и ускорения движущихся тел системы. Для этого составляют уравнение (207) для произвольного перемещении системы и дифференцируют по времени обе части полученного равенства.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:

