Теорема об изменении кинетической энергии материальной системы
Так как ускорение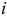 
-ых точек материальной системы
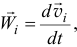
то основные уравнения динамики для этих точек будут
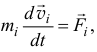
где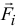 
— равнодействующая сил, приложенных 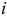-й точке. Умножим скалярно левую и правую части этого равенства на 
:
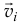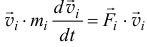
и введем слева вектор 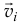под знак дифференциала, а справа учтем, что
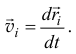
Получим
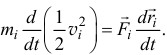
Или окончательно
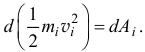
Сложив такие равенства, составленные для всех точек системы, получим:
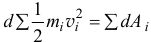
или
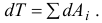
Проинтегрируем затем на переходе системы из одного положения в другое:
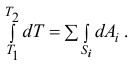
Получим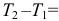 
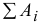. Запишем результат в виде
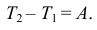
Это значит, изменение кинетической энергии движущейся материальной системы при переходе ее из одного положения в другое равно сумме работ сил, приложенных к системе, на этом переходе.
Замечания к теореме.
- Нетрудно убедиться, что реакции связей без трения работу не совершают. Поэтому при использовании теоремы в этом случае учитываются только активные, задаваемые силы (см. XIV, §1).
- Внутренние силы, вообще говоря, учитывать надо, несмотря на то, что сумма их равна нулю. Простой пример: две точки, соединенные пружиной. При изменении расстояния между точками упругие силы, приложенные к точкам, будут совершать работу. Но если система состоит из абсолютно твердых тел и связи между ними неизменяемые, неупругие, идеальные, то работа внутренних сил будет равна нулю и их можно не учитывать и вообще не показывать на расчетной схеме.
Теорему об изменении кинетической энергии удобно использовать при решении задач, в которых требуется установить зависимость между скоростями и перемещениями тел.
Эта теория взята со страницы помощи с решением заданий по теоретической механики, там найдёте другие лекции и примеры решения задач или сможете заказать онлайн помощь:
Помощь по теоретической механике
Кстати возможно вам будут полезны эти страницы:
| Потенциальная энергия |
| Кинетическая энергия |
| Закон сохранения энергии |
| Принцип Даламбера |
