Теорема об изменении кинетического момента системы
Возьмем какой-нибудь неподвижный центр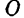 
и применим к одной 
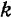-й точке системы теорему об изменении момента ее количества движения относительно этого центра. По формуле (171) будем иметь:
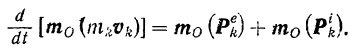
Составляя аналогичные равенства для всех точек системы и суммируя их почленно, получим:
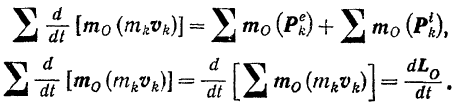
По установленному ранее (стр. 280), главный момент всех внутренних сил системы относительно произвольного центра всегда равен нулю:
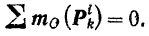
Подставляя значения (II) и (III) в равенство (I), окончательно получаем:
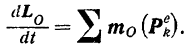
Производная по времени от кинетического момента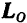 
системы относительно какого-либо центра 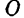равна главному моменту всех внешних сил, действующих на систему, относительно того же центра.
Проектируя векторное равенство (178) на какую-либо неподвижную ось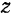 
, проходящую через точку 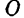, получим:
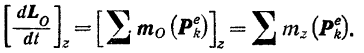
Производная no времени от кинетического момента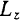 
системы относительно какой-либо неподвижной оси 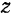равна главному моменту всех внешних сил, действующих на систему, относительно той же оси.
Рассмотрим теперь теорему об изменении кинетического момента системы в ее относительном движении по отношению к центру масс.
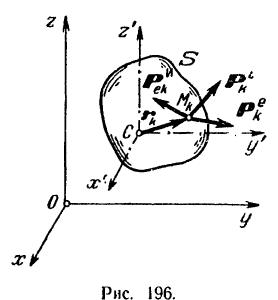
Пусть некоторая система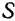 
материальных точек (рис. 196) движется относительно неподвижных осей координат 
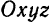. Примем центр 
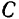масс системы за начало новой системы координат 
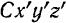, движущихся вместе с системой 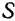, но остающихся все время параллельными относительно неподвижных осей 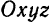. Следовательно, оси 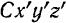движутся поступательно относительно неподвижных осей с ускорением 
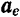, равным ускорению центра 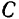масс системы.
Найдем закон изменения кинетического момента системы относительно подвижных осей 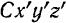, проходящих через центр масс. Как было установлено в § 73, уравнениям динамики для относительного движения точки можно придать вид уравнений динамики для ее абсолютного движения, если к силам, действующим на точку, добавить соответствующие силы инерции этой точки.
Так как переносное движение (движение осей 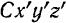) есть движение поступательное, то кориолисово 
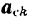, а ускорение и кориолисова сила инерции 
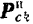для всех точек системы равны нулю.
Переносные ускорения 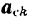у всех точек системы равны ускорению 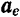ее центра масс. Следовательно, переносная сила инерции точки 
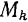(рис. 196) системы
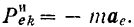
Применяя установленную выше теорему к относительному движению системы по отношению к центру масс, можно записать:
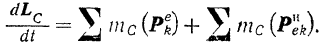
Здесь
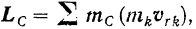
где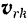 
— скорость 
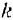-й точки системы по отношению к подвижной системе отсчета .
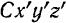По формуле (19) (см. § 19) для момента силы 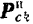относительно центра 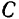будем иметь:
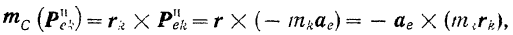
где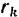 
— радиус-вектор точки 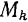(рис. 196), проведенный из центра 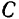масс.
Следовательно,
По формуле (138′) имеем
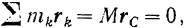
так как точка 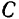является началом координат для осей 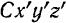и для нее радиус-вектор
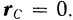
Таким образом, получаем, что
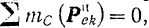
и равенство (1) принимает вид
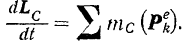
Полученное уравнение полностью аналогично уравнению (178), выражающему теорему об изменении кинетического момента системы относительно неподвижного центра .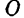
Проектируя векторное равенство (180) на координатные ос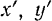и 
и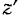 
проходящие через центр 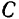масс системы, мы также получим уравнения, аналогичные уравнениям (179).
Таким образом, теорема об изменении кинетического момента системы как относительно неподвижного центра, так и относительно неподвижной оси приложила в той же самой форме и к относительному движению системы по отношению к осям координат, движущимся поступательно вместе с центром масс системы.
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
