Теорема об изменении главного вектора количеств движения системы материальных точек

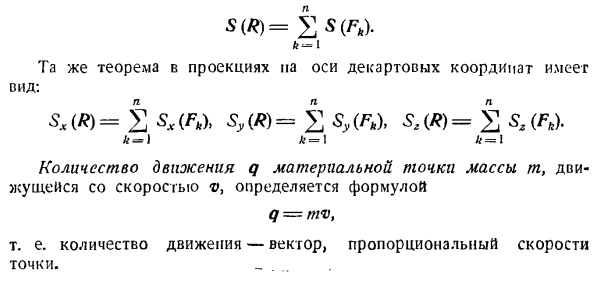
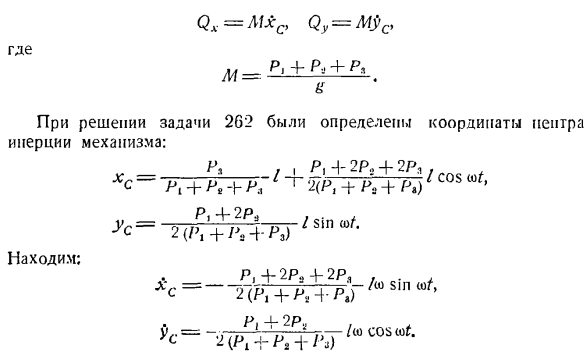
Теорема об изменении главного вектора количеств движения системы материальных точек

• Теорема об изменении главного вектора импульса системы масс 1°.Импульс силы. Основной вектор импульса системы масс. Импульс силы F, действующей в течение периода t%, определяется по формуле: / о S = J Fdt. Одиннадцать Если величина и направление импульса силы определенной силы постоянны Ы =Ф(Т1-tl). Проекция импульса силы на ось декартовой координаты равна: t * h H Sx = \ F * di> sv = \ Fydt> Sg = \ F2dt、 11 часов / 1 Где S-проекция SJ ^ Syj-r A Fxt Fy, а Pr-проекция модуля силы F. импульс ы = я / Си + с} + Си Направляющий Косинус определяется по формуле. потому что(Х,

Х)= СГ, потому что(Г, потому что (Р, С)= 5J, он. Единичный импульс силы: кг секунда. Импульс равнодействующей силы за определенный период равен векторной сумме импульсов составляющих сил того же периода ТУ2-ту, где V = г(ФК）、 н — м£\ = 2 а） Используя теорему об изменении импульса массовой точки, мы можем решить задачу, которая содержится как в количестве данных, так и в неизвестных: массе массовой точки m,

Результирующая теорема импульса. Людмила Фирмаль

скорости движения точки в первый и последний моменты времени и силе, приложенной к массовой точке, и временном интервале их действия. Вычислить импульс силы по формуле S = \ Fdt Л Обратите внимание на зависимость силы от времени. То есть в случае силы, зависящей от координат и скорости, необходимо знать законы движения. Задача применения теоремы к изменению импульса массовой точки должна решаться в следующем порядке:

1) на рисунке показаны все силы, приложенные к важным точкам, то есть указанная сила и сила реакции связывания (применен принцип связывающего иммунитета). 2) Выберите систему координат. 3) Напишите теорему об изменении импульса массы точек в проекции на эти оси： н — t * 1 = 2 к = ту.2-ту {= в Сы(ФК) т м = я 4) а) в задаче необходимо рассчитать проекцию импульса силы по формуле, когда необходимо определить начальную или конечную скорость точки изменения закона силы и период ее действия. / а ’а’ а ЗХ = \ Fxdt, Св = \ Fydt, с; = \ Ф; ДТ Ти Ти Ти Ти Ти И присвоить

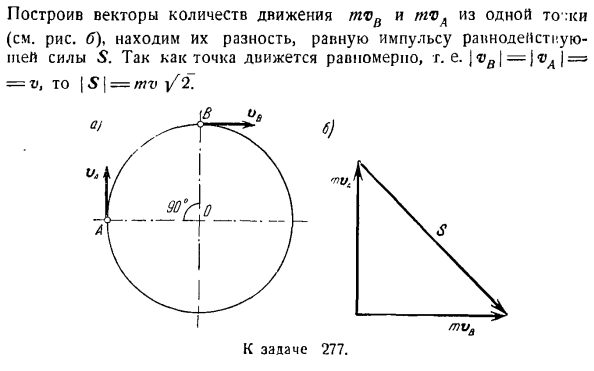
• их значение r 3 ’уравнению предыдущего абзаца, чтобы определить нужную проекцию скорости точек. Б) если необходимо определить одну из постоянных сил, приложенных к точке массы по условиям задачи, то в этом случае、 Модель: SX = FX(для Л> — Сы = ФГ(т — ф),= ФЗ(1, — х). Выпуск 277.Под действием системы определенных сил материальная точка массой m равномерно движется по окружности со скоростью V. При перемещении материальной точки из точки А в точку Б по дуге из 4 кругов за 1 минуту определяется

результирующий импульс этой системы сил. Решение. Примените теорему к изменению числа дней важных точек. Мет-МВ \ = С. С-бутадиен-нитрильный каучук, и mvx = МВА％ С МВ в МВ. Путем построения векторов импульса m / vD и mvA из одного и того же (См. рисунок b) Y найти разность, равную начальному импульсу силы. Поскольку точки движутся равномерно, то есть\ vB \ = / ^®д / = Цель 277. Выпуск 278.Груз опускается на шероховатую наклонную плоскость, расположенную под половиной угла а к горизонтальной плоскости; / — коэффициент трения груза, скользящего по наклонной плоскости

At во-первых, скорость груза была равна V. Людмила Фирмаль

plane.  Сколько будет стоить скорость груза в два раза? Решение. Покажем силу, приложенную к грузу: P-нагрузка, R-нормальная реактивная сила самолета, Fy c — сила трения груза, скользящего по плоскости, и тогда задача 278.Футов с = ФН = ФП, потому что Направьте ось x вниз вдоль наклонной плоскости. опишите теорему об изменении импульса точки масс в проекции на ось X. н МВ ^ — mvXx = г ^ Зх (ФК). к = \ В зависимости от состояния задачи, V \ x = v> v <ix = 2v. потому что все силы, приложенные к женихам, постоянны、 Н. Н. Н. Если Sx (Fk)= 2,

FkxM = {Ps \ no. — FJiC)а / = в — * (грех-й потому что） Я Где Дt-необходимое время interval. So … ДТ 2МВ-РНВ == Р (грех-/ соз а) 、 ВС \ 44 \ 4В \ 1мв. WWx К выпуску 279. Откуда в г(грех а — / соз а)’ Выпуск 279.Жесткое тело массой P начинает двигаться из стационарного состояния на шероховатую горизонтальную плоскость под действием силы f’f = at, пропорциональной времени. Где a-константа. Если коэффициент трения геля о горизонтальную плоскость b равен/,

то какую скорость набирает гель через t секунд после начала движения? Решение. Объясним силу, приложенную к телу: P-масса тела, F-движущая сила по модулю F = at, R-реактивная сила, нормальная к горизонтальной плоскости, FTc-сила трения скольжения объекта в горизонтальной плоскости, Frc = / P направьте ось x горизонтально вправо. опишите теорему об изменении импульса точки масс в проекции на ось X. н mvix-mvlx = ^ Зх(ФК \ k = I

vlx = 0, начиная с первого момента, когда тело неподвижно. Викс = ЧХ. Где vx-проекция желаемой скорости на ось X. сумма проекций импульсов всех сил на ось Х равна、 (б)= {РДЛ- / МК-Т = {atdtбыл-ФПТ = ^ — / ПЛ I U 0 Следовательно, где 3°.Теорема (интегральная форма) об изменении главного вектора импульса системы масс. Изменение основного вектора импульса материальной точечной системы через определенные интервалы времени Временной поток равен

векторной сумме импульсов всех внешних сил системы за один и тот же период. Q * — Qi = 2 5 Я Та же теорема, что и проекция на ось декартовых координат Смотреть： Н. Н. Н. СМО * 2 ЗХ Щ,,- Qyy = 2 с、 K в = I Л = 1 Я; 5.(FJ）、 ч = я Иначе говоря Если вы хотите получить наилучшие результаты, вы можете сделать это с помощью следующих методов: обратите внимание, что сумма импульсов

находится внутри н Из них сила системы всегда равна пуле: 2 = m Сила непосредственно не влияет на изменение основного вектора импульса системы масс. Отсутствие внутренних сил в формулировке теоремы об изменении главного вектора импульса в материальной точечной системе значительно упрощает решение соответствующей задачи. Теорема ZGA обычно применяется в случае непрерывных сред (см. теорему Эйлера ниже). В случае сохранения ключевых векторов

системы и массы импульса точки. Если векторная сумма импульса внешней силы системы равна пуле, то основной вектор импульса системы материальной точки н То есть, если V S (Fek)= Q, то 4 = Qv к = I Если суммарная проекция импульса внешней силы на заданную ось равна нулю, то проекция основного вектора импульса движения системы на эту ось не изменяется. Например、 н Х ^ Ш =°>тогда Ку = qix по ^^Я Закон сохранения основного вектора импульса массовой

системы, или закон сохранения ее проекции, лучше всего применяется при решении задачи нахождения величин, в которых в данные включены масса материальной точки и скорость начального и конечного момента. Решите задачу используя закон сохранения основного вектора импульса в следующем порядке: 1) на рисунке показаны все внешние силы. 2) Выберите систему координат. 3) Напишите теорему об изменении главного вектора импульса системы масс в проекции на координатные оси、 4) сумма

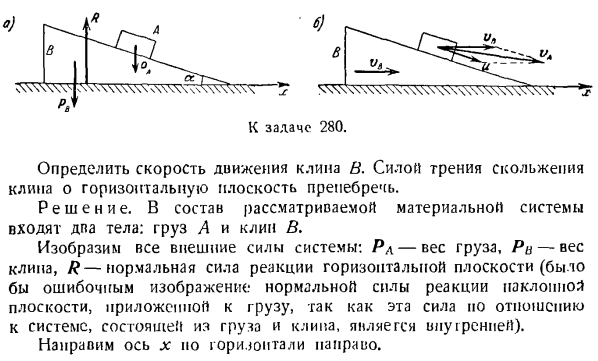
проекций импульсов внешней силы на ось н Равен нулю, например: V] Sx (fj)= 0 Нить между собой проекций на эту ось основного вектора величины движения системы в первый и последний момент, то есть, Н. Н. Н. Qix = Qix> Qix = Y tnkxki и Qijr = Y] mhXkv и от Б = я » м ^ ал Уравнение определяет искомое значение. Задача 280.Материальная система состоит из нагрузки массы RAau. Лежащий на наклонной плоскости Клина в груз Пу, расположенный под углом а к horizontal. At в первый момент система была остановлена. Затем

груз и стал скользить по наклонной плоскости с относительной скоростью. С (Р)=£С(Ф>). м-я Однако форма проективной теоремы на оси декартовых координат имеет вид: фута-Джей фут = я фут = я Импульс q массы m массы движущейся со скоростью v равен м = МВ、 То есть импульс-это вектор, пропорциональный скорости точки. 0) 1 B i R \ r ^ A 6) B ^- з \ з \ \ \ 4В\\\\\\ ч \ \ \ \ ч-оч \ \ \ \ \ \ \ \ ’ Дж. ч \ \ \ ч\\\\\\\\ ХХХХ \ ч \ hchuchch—гг Переходим к выпуску 280. Клин B определяет скорость. Игнорируйте силу скольжения зажима

в горизонтальной плоскости. Решение. Рассматриваемая материальная система включает в себя 2 корпуса: груз а и зажим В. Обозначим все внешние силы системы: Rl-вес груза, Rc-вес зажима, а R-нормальная сила реакции горизонтальной плоскости (эта сила связана с системой, состоящей из груза, поэтому ошибочно представлять силу реакции нормальной силы наклона, приложенной к грузу). направьте ось x горизонтально вправо. * ……….. «Л».- Напишите теорему об изменении главного вектора импульса системы

материальных точек в проекции на ось G. н Цюй 2 $ ЛП). фут = 1 потому что суммарная проекция всех внешних сил на ось Х равна нулю： н 2 Fkx = 0, сумма проекции импульса всех внешних сил на b-1 Эта ось также равна нулю： S (Fl)= V ’(F’xdt f; x) dt = 0 фут = я фут 1/, т {м = я И затем… Цюй-Игры Qix = Т. е. М * х = красивый. Поэтому проекция главного вектора импульса системы на ось x может быть сохранена. В первый момент система была неподвижна. То есть Q, x = 0.Вычислите проекцию главного вектора импульса системы

в определенный момент на ось X. Предположим, что клин B движется вправо с соответствующей скоростью vd. To найти скорость движения груза A, точка vn = ve — {- <vr. e.< vr = u. So,=(см. Рисунок B) и Прививки = Vfix + УБ

Теперь мы можем рассчитать проекцию импульса системы на ось x основного вектора. Р П Игры qix = mAvAx-Джей-mBvHx ==(курсоры + и коза) VDX в \ Как показано, Q. lx = Qlj(то есть、 Г(сырья, промышленности и энергетики + «, потому что а)+» г = Откуда Джи! д * = — п, п С потому что. ’Л’ Знак минус указывает на то, что клин B фактически движется влево. То есть вектор r-MCV2; = Oh、 Куда? Ms = p1a1g / 1 = p. 2a, и>; 5) Определите искомое значение по формуле, составленной в предыдущем пункте. Задача 282.Поток воды течет

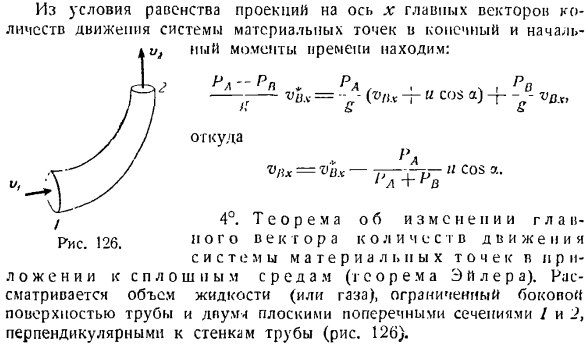
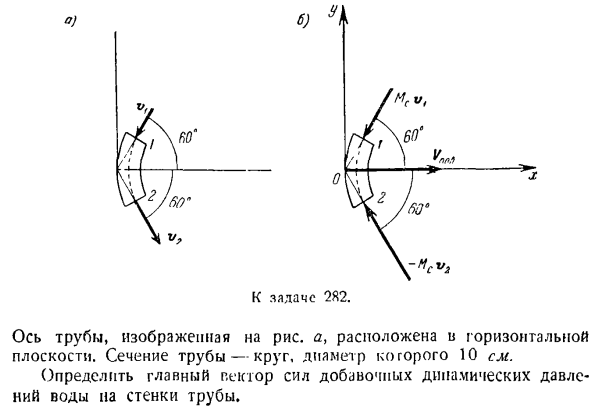
по изогнутым трубам. Прямая часть изогнутой трубы образует угол 120 при скорости 120 Mjceic. Проблема в 2Н2. Ось трубы а, показанная на рисунке, находится в горизонтальной плоскости. Поперечное сечение трубы представляет собой круг диаметром 10 см. Труба определяет основной вектор силы, который принимает дополнительное динамическое давление воды на стенку. Да.） 6) ч

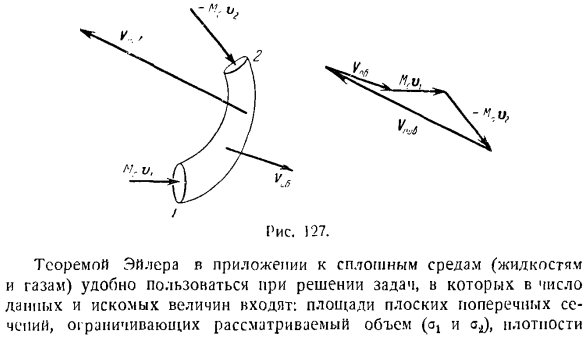
Решение. Используйте теорему Эйлера в качестве приложения к непрерывным средам. Схема и показывает вид трубы в плане. Объем-это сила тяжести воды, перпендикулярная плоскости рисунка. Поверхность-это сила реакции стенки трубы, приложенная к частицам воды. После того как вы определили основной вектор силы реакции стенки трубы, найдите нужный основной вектор

дополнительного динамического давления воды на стенку трубы по принципу равного действия и реакции. Укажите вектор 2-го движения воды, протекающей по участкам труб 1 и 2 в целевой объем (см. Рисунок Б). 2-я масса воды, то есть масса воды, протекающей через участок трубы за 1 секунду МС = г ав ’ Где 1-удельный вес воды, площадь поперечного сечения трубы, а V-коэффициент скорости движения воды в трубе. направьте ось x горизонтально вправо, а ось y вертикально вверх. Опишите теорему Эйлера в проекциях оси x и Y. КБ х + ^ ФВ-+ МС * 1х-ср. «он = Vo6 г + ^ ПОВ г + MLVly-мМЕ = В этом

случае вектор Vo6 перпендикулярен оси x и оси y, поэтому: Кровь ж-ВКМ потому что 60°-ВКМ потому что 60 «= 0,Л / n0B в-ВКМ соѕ 30°+ СОЭ в COS 30°= 0 Величина движения равна 1 от масштаба движения точки массы. Проекция импульса точки массы на ось декартовой координаты выглядит следующим образом: модель QX = mvx%тип qy = мвы, К2 = МВЗ Или qx = mx, qy = mt, QZ-модуль импульса mt Направляющий знак： потому что {?Cq)= q*, cos {y ^ q) = b. t cos = K единица измерения импульса: кг * сек Основными векторами

импульса в системе масс являются: n. n. n. М = х Ин = б tnkVb = МС / ? = Я Это векторная сумма импульсов точек материальной системы, равная произведению массы системы на скорость центра инерции. Проекция главного вектора импульса системы масс на ось декартовой координаты задается формулой: п п п п п Qx =Щхк = Mxcqq, = 2 Rritjk = My a 2 mkih = MTC FT = I K = ） Где Q = QJ + QJ + QA (В этом случае индикатор скорости отбрасывается, так как он равен\ vi \ = \ vi \ = v) 1 Umh = 2Mc cos 60°, VnoBy =0.Таким образом, основной вектор

дополнительных динамических реакций стенки Труба направлена параллельно оси x (см. Рисунок b). Это отличный способ начать свой день.、 ё И затем… ^ пов = 2 г-Кин Косинус 60°. Условие 7 = 1 кг / дм3, = 100 ДМ / с、 98,1 ДМ / с подстановка этих значений дает / pov = 80,6 кг. Основной вектор силы дополнительного динамического давления воды стенки трубы N направлен в противоположную сторону от Vnoa, то есть горизонтально влево, с равной величиной. Задача 283. Со скоростью 12 м / с из резервуара, заполненного водой, вытекает поток воды. Диаметр выходного отверстия d = 4 С. И. Определите

общую горизонтальную реакцию стенок резервуара. Понижение уровня воды в баке игнорируется. Решение. Используйте теорему Эйлера в качестве приложения к непрерывным средам. Объем-это сила тяжести частиц воды. Поверхность-сила реакции стенки резервуара. 2-й импульс движения секции / воды равен нулю, поскольку он игнорирует скорость снижения уровня воды в резервуаре. Вектор от 2 секунд до 2 секунд движения воды, проходящей через секцию 2, направлен внутрь рассматриваемого

объема воды, то есть горизонтально влево. На рисунке 6 показана выбранная ось декартовой координаты xy. я J — — — ^ ✓- М и п： Выпуск 283. Теорема Эйлера формат проекции на ось x это немного похоже на то. v » f VM x-Mscrx-MtVu = 0. В этом случае Vo6x и Mcv, v равны нулю, поэтому это выглядит так:^ pov * — = 0, т. е. 1 / pv x = Mcv. Масса 2-й воды будет равна П1. = 7 cv, где y-удельный вес О Воды, где o-площадь поперечного сечения 2, v-коэффициент скорости течения, то есть Vll0nx = av*.в этой задаче Q t = 1 кг [() m \ a = 0,13 ДМ V = 120 ДМ, ’ сек g = 98, l ДМ / с \ Подставляя числа, получаем желаемое суммарное

сложение горизонтального модуля силы реакции стенки резервуара Ключевой векторный модуль импульса системы масс Q = Qi + Qz- Направляющий знак： потому что(^ Р с = 0, следовательно, м = Aivc = 0.Поэтому главное Вектор импульса в этом случае не зависит от угловой скорости и равен пулю. Задача 274.Если центр тяжести колеса движется по закону xr-at, то определяют основной вектор

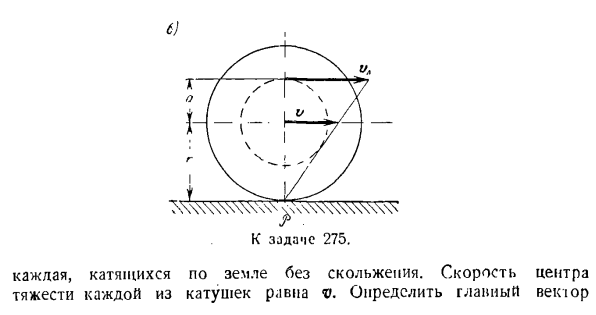
импульса колеса массой P, которое катится по прямому рельсу. .—— Решение. Основной вектор/ Количество движений колеса/ \ Переходим к выпуску 274. Другими словами, он горизонтально ориентирован вправо, а вес Py перемещается горизонтально с весом P9 и радиусом r витков B и D Вопрос-МВ Где M-масса, а vc-скорость. Центр тяжести колеса. В рассматриваемом случае vc = xc-a, то есть зет Вектор Q-ковариат 0C> Задача 275. Lalk A от 2 направо

Катитесь по земле, не скользя. Скорость каждой катушки равна V. определим основную Центральный век Каждый, гравитация Величина перемещения системы. Луч находится на расстоянии r-f-a от Земли (см. Рисунок). Решение. Основной вектор импульса системы： Где Qa-ключевой вектор импульса пучка A, QB и QD-ключевые векторы импульса катушки B и D. У нас есть： = = = Предполагая, что мгновенный центр скорости (cP) каждой катушки находится в точке контакта между катушкой и землей (см. Рисунок 0),

можно увидеть следующее: V = — 1-V. Л р р Так… I = Gchl + = 1 (—Pj-2] v. * n’g \ r 1 * 1） Итак, направление главного вектора импульса системы совпадает с направлением движения луча. Задача 276.Задача 262 определяет основной вектор для величины перемещения исследуемого коромысла механизма. Нерешенный. Проекция основного вектора количественного движения механизма на ось декартовой координаты задается формулой： Модель QX = mxc по> Тип qy = кесарева Куда? м = р-+ р+ р ’. О При решении задачи 2G2 были определены координаты центра инерции механизма. Р,…, П,+ 2стр +

2Pa,-пт + Р2 + я; «Г 2 (П+ Н+ ПБ) соя Выяснить; П 4-2 П 2(/>,’+З’.+Т^ ’ Общ.> 1rt + д + п, р 51n ’ Так… Модель QX = Косс = — — — — ^-3 / ко греху «）/、 М ^ = MJfc = я * потому что искусство. Модуль основного вектора величины перемещения коромысла механизма Г =] / и QX + КЖ = 2 /(Висконсин Пи + + СШ * sin1″РФ +(п — ф 2Pj) в cos2Ш/. косинус угла, образующего ось jc и вектор Q / Бык (Пи-1-Син потому что (ДГ, с?)= 7 ^ = — — — 1 О Альвис ^ я ч-л-HRLU siriJ ’о +(ф; — г»»’ 2°.Теорема (интегральная форма) об изменении импульса точки масс. Изменение импульса

материала! Точки определенного периода времени равны векторной сумме силовых импульсов, приложенных к точкам на одном и том же временном интервале. н Р1-к1 = 2 с(ФК), к = 1 Где qx-начальный момент//, а q. 2-соответствует моменту завершения той же теоремы, что и проекция на ось декартовой координаты имеет следующий вид. н МХ-Mxi по = Х (ф) > к = I

Смотрите также:

Предмет теоретическая механика

Дифференциальные уравнения движения системы материальных точек	Теорема об изменении главного момента количеств движения системы материальных точек. Моменты инерции твердых тел
Теорема о движении центра инерции системы материальных точек	Динамика плоского движения твердого тела