Оглавление:






Теорема об изменении главного момента количеств движения системы материальных точек в приложении к мгновенным силам
- Приращение главного момента импульса материальной системы относительно неподвижного центра при ударе равно векторной сумме моментов относительно того же центра импульса внешней мгновенной силы. Или проекция на ось декартовых координат. Та же теорема об объекте, вращающемся вокруг неподвижной оси 2, Формула н г х ПГ ч 1. Так, воздействие импульса на объект, вращающийся вокруг неподвижной оси, проявляется в постепенном изменении его угловой скорости.
Эта теорема должна быть использована для решения задачи о воздействии на тело, вращающееся вокруг неподвижной оси, когда полученные данные и величины включают импульс импульса, момент инерции тела относительно оси вращения, а также угловую скорость тела в начале и конце воздействия. Задачу целесообразно выполнять в следующем порядке с помощью теоремы об изменении основного момента импульса в движении, к которому приложена мгновенная сила. 1 Нарисуйте внешний ударный импульс на рисунке 2 вычислить сумму моментов импульса то есть импульсов всех внешних мгновенных сил относительно оси вращения тела 2.
В основе динамики, как и других паук, лежат физические законы—аксиомы, подтверждаемые многовековой практической деятельностью человека. Людмила Фирмаль
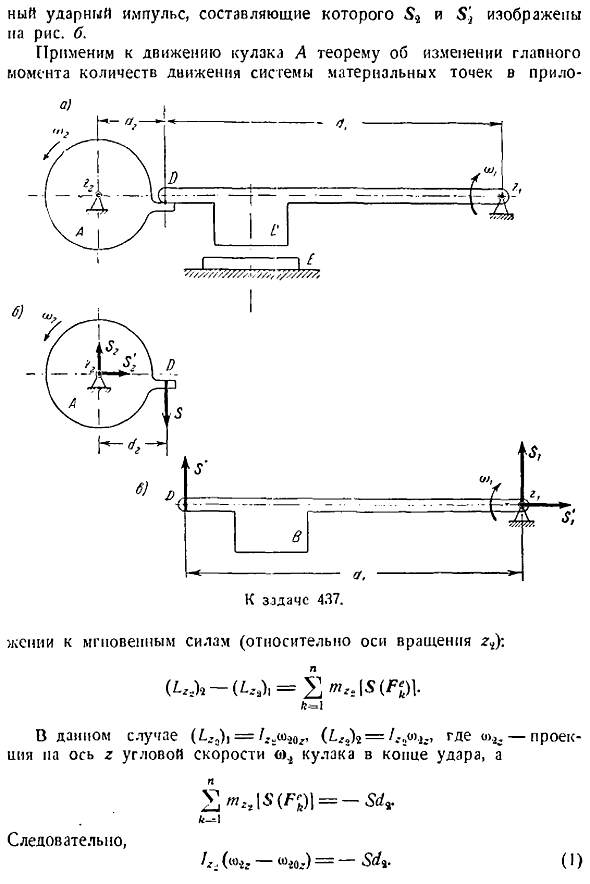
Подставить полученный в предыдущем пункте результат в уравнение н Вт И5 б Определите желаемое значение. Задача 437. Па Рис. Вес p штемпеля b равен shown. It приводится в движение массой p3 кулак а и неподвижной осью 2. Повернись кругом. После нажатия кулаком выступа в точке Р штампа, штамп Б поднимается при вращении вокруг неподвижной оси 2Р. Пройдя через выступ кулака, штамп падает на заготовку Е. Ось перпендикулярна плоскости рисунка. Расстояние точек р до этих осей вращения равно r, и в момент начала удара кулака выбрасыванием о штамп в точке О, кулак имел угловую скорость ov, а штамп был неподвижен.
Радиус инерции штампа относительно главной оси равен p, — радиус инерции кулака относительно оси равен 2. Определите угловую скорость штампа В конце штриха посчитайте а Удар неупругий, если l. Решение. Эта материальная система состоит из 2-х тел кулака а и штампа Б. Рассмотрим движения каждого тела в отдельности. Во время столкновения импульс снаряда 5 добавляется к кулаку а в точке О со стороны штампа b. in в этом случае на опоре возникает реактивный ударный импульс. 6.
Применим к движению кулака теорему об изменении главного момента импульса материальной точечной системы а Уменьшение до мгновенной силы относительно оси вращения r y В этом случае, dga, 2 2 Изменение угловой скорости кулака по оси z в конце столкновения, и 2Х, Я 1 — че — 1 Так. .4 .- ч 0 г — 1 Рассмотрим перемещение штампа В .
- При ударе штамп в прикладывается к точке О со стороны кулака а, при ударном импульсе 5, а 8 −8, исходя из принципа равенства действия и реакции. Когда подвергаются воздействию, происходит реактивных ударных импульсов в поддержке .Его компонент равен 1 и показан на рисунке 1 .с .Применить к движению штампа для оси 2 1 применить к мгновенной силе теорему об изменении основного момента импульса материальной точечной системы Л В этом случае Дг, Поскольку штамп в начале удара был неподвижным, oi, где проекция нужного угла на ось z Скорость o, штамп на конце неупругого удара, и 5 Е1 5ч .С Так .. 2 Дано m. e.
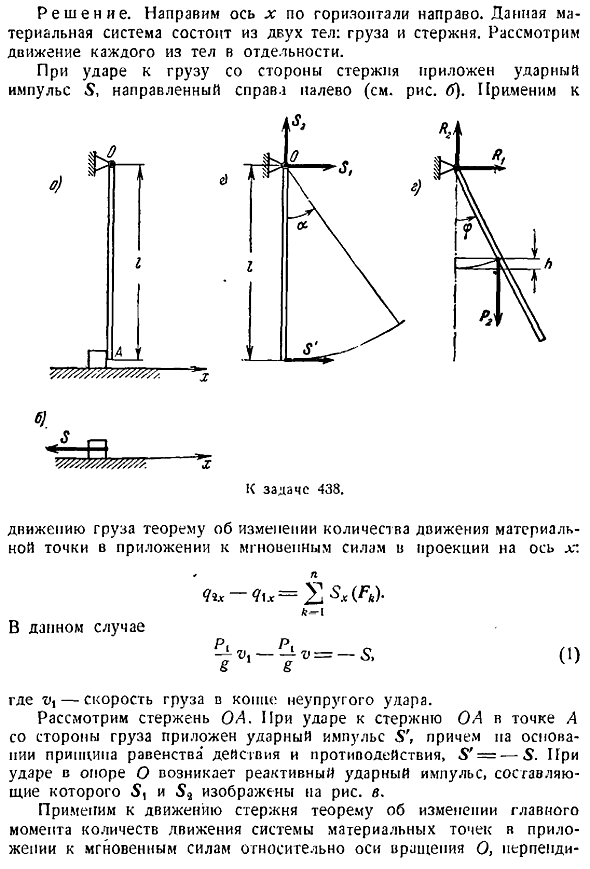
Исключим величины и y из системы формул i и 2 и определим проекцию штампа b на искомую угловую скорость o1 к оси 2. В конце хода Р п п п Х1 — п Итак, в конце концов 5 литров ВТ ХР Р g, x r. Rz 0 1г Проблема 438. At в момент столкновения с подвешенным вертикальным стержнем ОА, возникает скорость т в грузе массой pb, движущемся вправо вдоль горизонтальной плоскости. Нарисовать. Масса стержня p4, длина стержня. Учтите, что воздействие нагрузки на стержень является неупругим. Решение. Направьте ось x горизонтально вправо. Эта материальная система состоит из 2-х корпусов груза и стержней. Рассмотрим движения каждого тела в отдельности.
Начало абсолютной системы координат принимается в центре Солнца, а оси направляются на три отдаленные звезды. Людмила Фирмаль
При столкновении ударный импульс 5 прикладывается к нагрузке со стороны стержня и направляется справа налево см. Рисунок Б. Применимый Голы 438 теорема переноса груза об изменении импульса материальной точки, приложенного к мгновенной силе в проекции на ось x Я х х Я В этом деле Здесь скорость нагрузки в экземпляре неупругого удара. Рассмотрим стержень ОА ударьте стержень ОА в точке А со стороны нагрузки, импульс удара приложен, действие и реакция, 8 —5 по принципу равенства. При столкновении с опорой о возникает реактивный ударный импульс, составляющая которого равна 5, как показано на рисунке 1. С.
К движению стержня применим теорему об изменении главного момента импульса материальной точечной системы, к которой приложена мгновенная сила относительно оси вращения o, перпети 2. Рисунок на плоскости кулярпоя — Шаг u. M0 5. Е 1 В этом деле o0r 0, m0 8 1 к 1 Так. .о 01 Дали а .И исключить 151 Y, V, 8 и b7 из системы уравнений I и 2, а также определить проекцию угловой скорости 1 1 на ось z стержня ОА в конце удара .Р .п .P 2 Момент инерции стержня 0 .так .. ЦИРКОНИЙ И — СП. Х-Р.
Импульс удара 5 определяется путем подстановки значения o1r из 3 в i или 2. Мы это выясним С— г 6 дюймов ЗР, 4-р, Для вычисления максимального угла отклонения стержня от вертикального положения применим теорему об изменении кинетической энергии материальной точечной системы. L-1 Угловая скорость стержня e в этом случае она находится в конце начального удара при последующем движении, а угловая скорость при максимальном отклонении равна нулю. Поддерживающая реакция составляющих элементов и работа p2 равна нулю, а работа силы тяжести p задается формулой a p — p4y. Го— 1-Вау См. Рисунок d. Итак.
Смотрите также:
Предмет теоретическая механика
| Общие замечания по решению задач динамики | Потеря кинетической энергии при ударе двух тел |
| Специальные задачи динамики. Удар | Удар по телу, вращающемуся вокруг неподвижной оси |

