Оглавление:

















































































































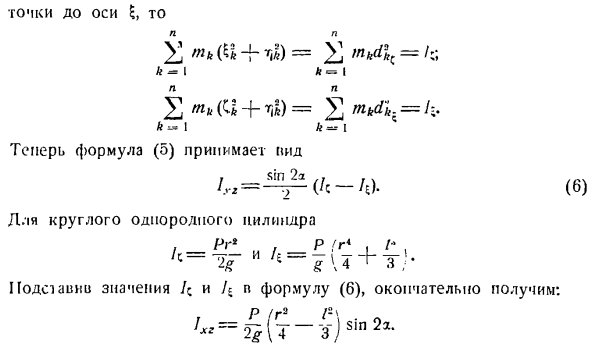





Теорема об изменении главного момента количеств движения системы материальных точек. Моменты инерции твердых тел
- Теорема об изменении главных моментов импульса материальной точечной системы. Момент инерции твердого тела 1°.Основной момент импульса материальной точечной системы. Момент / 0 импульса (момента движения) материальной точки относительно центра O является вектором, определяемым формулой. 1о = с GX Модуль этого вектора равен [/o / = mvh, где h-плечо (рис. 12 *) = у у9(к * — Ж*) = 0 поскольку это z / z k, это A = — — — t и B = 0.Конкретное решение принимает вид: х•、 ;; Грех< Здесь^ — ^ l ^ Ljilfll u =написать общее решение Дис Национальное уравнение(1): ? =?я-Р =С»,
потому что КТ-Ф-С * грехом * * — грех (•’) Определить константу C (и вычислить производную y для l: Costo/.(4 )) После замены начального условия:/ = 0, cp = 0 в(3) И t = 0, с φ= () (4), C,= 0 и C. 2 = — kjk ^- Таким образом, форма уравнений движения диска(3) имеет вид «=- Ш«^] Си «’ {т + е ^ Си» Вариант 6)&=, то есть рассмотрим случай резонанса. Ищем конкретное решение в следующем формате = грех у£ … )) Подставив (1) в (5), получим коэффициенты, равные левому и правому знакам и косинусам соответственно Часть уравнения. Получаем: a-0 и B = — следовательно、 Ф4= 5-A-t COSШ*, (6) Где h =
осле определения начальных условий движения Людмила Фирмаль
С учетом формул (2) и (6) запишем общее решение дифференциального уравнения (1) в следующем виде: СР = с \ совместное КТ + м грех КТ-я, потому что на. (7 )) если взять производную от o с ty, то она выглядит так: $ =- С, грех КТ + C2k потому что КЛ-это потому, что со / ^ / грех со /; (8) П, (7) t = 0, c = 0 и/ = 0、 6 = 0 n(8), C \ = 0 и C2 = m ^ r(потому что w = k).Принесите его сюда. С, и, наконец, получаем уравнение движения диска в случае со из уравнения (7), резонанса. Л. ч. И что? = $ 111 ко /—<т-т, потому что ко /、 ,I miy2g(Γ
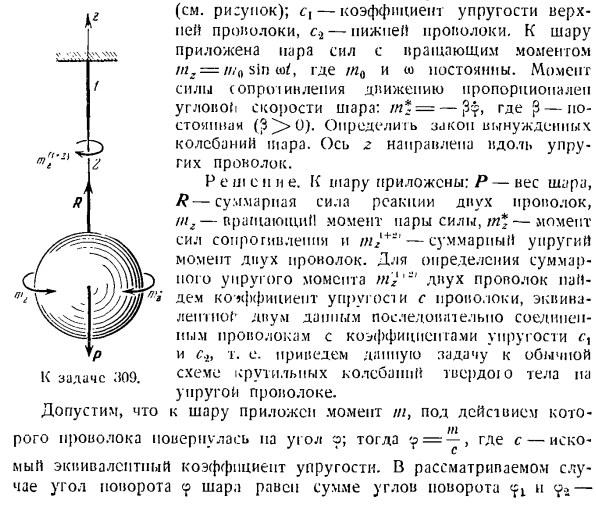
, RVT), 2d7lv, где » > = * =- J / y ’и^ = Переменная амплитуда вынужденной вибрации равна / о) Он увеличивается во времени пропорционально и ограниченным образом. Выпуск 309.Шарики веса P и радиуса r выполняют крутильную вибрацию с 2 эластичными проводами соединенными последовательно (См. фото); cx-модуль упругости верхнего провода, S. 2-нижнего провода. Пара сил приложена к шарику с крутящим моментом tg = b sin sin art. Где MQ и являются постоянными. Момент сопротивления движению
- пропорционален угловой скорости шара:/ n * = — является постоянной величиной(3]> 0).Определяет закон вынужденной вибрации контейнера. ось Z направлена вдоль упругой проволоки. Сопротивление, приложенное к шарику: P-вес шарика, R-общая сила реакции 2 проводов, tg-крутящий момент пары сил, tn * — момент сопротивления, T * * * ’ — общий момент упругости 2 проводов. Чтобы определить суммарный упругий момент 2 проводов m’j, найдите модуль упругости от провода, соответствующего 2 заданным последовательно Соединенным проводам с коэффициентами упругости.
Верхний провод и нижний провод соответственно нижний, то есть 9 =?* + т-2В / РС грех <от АКЛ грех ОИТ БКЛ потому что ТОФ = ч греха Вт Если приравнять коэффициенты левой и правой частей уравнения к синусу и Косинусу, то получим систему. А (к -до 9) -2 — (o ‘ 2)+ 2Llo)= 0、 。 Л (Л2-0 2М » ч откуда A = — / — и B =- (к-00-)-4-4 / 1: ‘о (/Г2-» о*) * + » 1 / I2u) в• Подставляя полученное значение<4 в уравнение(2), получаем: А (*—<О2). 2π<ол、 9 = 7H -,*, * >от греха Г— — — cos (оф. Для определения амплитуды вынужденных крутильных колебаний дано следующее: ч(К * — <О-)_ (/р-о ’-1)2 + 4 / и4″ а ~~ в C0S£ ’ = грех е. (Л2-от -) -+
Жесткое тело, подвешенное на упругой проволоке, совершает крутильные колебания под действием внешнего момента tn = f (/).Где f (t) — единственная периодическая функция периода x. Людмила Фирмаль
а= -, __ — подпалый£= — Дж. Итак, вынужденная крутильная вибрация шара происходит по гармоническому закону. Л. /. .2na> \ 9 = _ грех я мас-arctg-7-з-Т、 Куда? Для резонанса, то есть для w = / r, угловая амплитуда вынужденной крутильной вибрации шара равна Проблема 310 c-модуль упругости проволоки, а ее упругий момент пропорционален углу twist. tg= — сир. определить закон вынужденных крутильных
колебаний твердых тел при ориентации момента инерции вокруг оси z Если вы используете тождество cos y-cos a = 2 ^ sin2£ — sin * * j, вы получаете: = КДТ. Y sill2″ Давайте заменим его с Грех£= Грех Грех и г ■а ^ в грехе-Н COS и Дю < НЛ Вт 2 салат ромэн£ Где выражение(8) принимает вид: РФС = КДТ、 ф потому что Или Дю. = КДТ. Ф 1-Си Один sin2 * — грех * у Вдоль провода идет\ 2. ко!1гривлепия проигнорировала силу движения. Решение. Разверните m = f (t) в ряд Фурье(после проверки полноты условия Дирихле): (0 Мюррум.: м = F(Т) К выпуску 310. И затем И ф(0 = 2 + 2 C0S ж + Би греха я = я Куда? Два * К Как известно, коэффициенты ряда Фурье вычисляются, но、 т. в = 4 ^ /(0, потому что ДТО т. 4 Дж /(0С » н д ДТ、 Здесь.、/ = 0、1、2、… Напишите дифференциальное уравнение вращения вокруг оси G
твердого тела G. ’* ?=±м> л = я Потому что сила веса твердого тела и момент силы реакции против оси z провода равны нулю、 н £МЗ (футы)= МЗ + м = — С9-ф /(0- к-мне Используя формулу (1), получаем: И затем J_ 2 к = я 1 (Ф {) = — с <? + 2 «» б ^ я, потому что Би Син- В результате дифференциальное уравнение для вынужденных крутильных колебаний твердых тел принимает вид: Конечно.) = — c <p-1-n0Y (i, — cosШ — (- bt sinЫ) Или И £- Л-К’ — Я = Я — Г (а, потому что АО / — Ф sinЫ). (2) г * / — я Где / c «2= -.Как определить закон
вынужденного кручения ’з’ Левапиус нужен только для того, чтобы найти конкретное решение дифференциального уравнения (2). Ух… ) <Р = АО + х (<Аи C0S + Син / по to0-(3) я) Коэффициент А0,.4,-и Б、-(/ = 0、1,2、…для вычисления формулы(. Присвойте значение o из’$) выражению (2). Да. — /V 2 и-cos M + I; sin / W) — f£ 40-p Меня. меня. И — До Г(а (потому что / а)/〜Би грех х)= * = Дж К Я = + /; 2 потому что ыб (Син Сю (4) я = я Уравнивание постоянного члена, а также
коэффициентов соответствующих синуса и Косинуса левой и правой частей уравнения (4) приведет к тому, что: С, (К» -; в)=»;、 / = 0, 1, 2,… АиФ БТ и найти полурасчетное значение Формулы (3), формулы вынужденных крутильных колебаний твердых тел И (tocos м + если ^ Wsin ы). Меня. меня. Куда? О)=?Г1,= 7 -, а,= /(0 cosdtdt И затем И затем * Т = — С/( / ) sinШdt(1 = 0、1、2、… Т ОЖ
Твердое тело резонирует при следующих условиях: k * — / V = 0, где/ = 1, 2, 3,…, То есть η= .. Таким образом, если/ = 1, то есть если k = to, то возникает резонансная вибрация 1-го порядка、 для / = r2, то есть для U = 2sh, возникает резонансная вибрация 2-го порядка если / = a, то есть/==) возникает резонанс / / / / следующей вибрации.
Резонансные колебания низкого порядка наиболее опасны тем, что их величина уменьшается как на порядок величины 1 разряда, так и на порядок B {резонансные колебания возрастают. 7°.Теорема о методе пения головы и движении материальной системы имеет движение относительно центра инерции. Разложим движение точки масс системы на переносное поступательное движение вдоль координатных осей системы координат. Начало координат этой системы координат совмещено с центром инерции системы
и ее относительным движением относительно центра масс. inertia. In кроме того, теорема об изменении основного момента импульса материальной точечной системы, совершающей движение относительно центра инерции, имеет тот же вид, что и аналогичная теорема об абсолютном движении. н rILr в — д бизнес-ЗС( То есть производная по времени от основного момента импульса материальной системы относительно центра инерции системы в относительном движении в системе координат, поступательно
движущейся с центром инерции, является векторной суммой моментов внешних сил системы относительно центра инерции. Та же теорема о проекции на ось декартовых координат, где начало координат совпадает с центром инерции системы и постепенно перемещается вдоль центра инерции、 k ^ 1 k = I I Когда основной момент импульса материальной системы сохраняется в движении относительно центра инерции системы. Если векторная сумма моментов внешней силы относительно центра инерции равна нулю, то основные моменты импульса системы Материальные точки относительно центра инерции R система координатных осей, которые постепенно перемещаются вместе с центром инерции, остается неизменной. н Если V mc (Fk)= 0, то Lc постоянен, fe-1 Та же
теорема проекции на ось декартовых координат отображает ее начальную точку в центр инерции системы, который постепенно перемещается вместе с центром инерции. Формат такой: н V] Если mcx (Fk)= 0, Lcx является постоянным. Теорема об изменении главного момента импульса системы точек материи при относительном движении к центру инерции системы (в случае сохранения) является задачей динамики плоского движения твердого тела (см. Следующий раздел)и свободного движения твердого тела, т. е. в этих случаях движение переносного тела можно разобрать. Задача 311.Акробат, делая сальто, выталкивает ноги из земли, и в первый момент угловой скорости o> = = 1 об / мин он сообщает себе о горизонтальной оси, проходящей через центр gravity. In в этом случае момент инерции
акробата вокруг оси травмированного лица/,= 1,5 kg-m-sec1.To увеличив угловую скорость в полете, акробат прижимает ноги и руки к туловищу, уменьшая момент инерции до величины/ 2 = 0,5 кг•м * сек*. Определить угол поворота акробата вокруг горизонтальной оси во время полета. Игнорируйте сопротивление движению. Решение. Внешняя сила, действующая на фигуру высшего пилотажа в полете, — это только ее вес. Движение акробата во время сальто затруднено. Если разложить на поступательное движение вместе
с относительным вращением горизонтальной оси x через центр инерции и центр инерции, то можно воспользоваться теоремой об изменении главного момента импульса материальной точечной системы при относительном движении вдоль этой оси. к = 1 Поскольку горизонтальная ось x проходит через центр тяжести акробата, момент силы тяжести акробата на этой оси равен Чтобы zero. As результат,= 0 и!. Cx всегда, то есть LWx = Lhx. Поэтому относительное движение материальной точки может поддерживать
первичный момент в объеме движения системы. Licx == / 4co, go / jto,= откуда ok2= -’ — («>,. Если вы назначите число, это будет W4 = 3 об / мин: секунды. 8 \ момент инерции и эллипсоид. Момент инерции твердого тела относительно оси L, проходящей через данную точку, определяется по формуле Дл -!Потому что Х-СL-и J-1ycosr} — Джей — zcos \ ’ 2? 2 / год cos t3 cos? — — Лл \ 2х, потому что 7 я-2fxy потому что, потому что п、 Где a, p и y-оси x, _y и. G и ось/.Это угол между ними, и момент инерции рассчитывается в этой связи
Твердое тело (рис. 130),/ g и / lz-осевые моменты инерции твердого тела!! ксити. и! Гх-центробежный момент инерции твердого геля, определяемый по формуле Н. Н. Н. lxy = х ПФС FCV на^. 1У = Йи tkUk?> k = I Ага. k = I В отличие от осевого момента инерции твердых тел, 1X, 1y.! Г. Они всегда положительные, центробежные моменты инерции могут быть и отрицательными, а в некоторых случаях они могут быть равны пулям. Для непрерывного распределения Мухрамовских бытовых дистанционных центробежных моментов инерции / Ху Вычисляется масса однородного твердого тела — Вт \ В) zxdVt
yzdV、/ Где M-масса твердого тела, V-его объем, dV-объем основания. Интеграция является общей для всех объемов твердых тел. Для непрерывного распределения массы в однородной пластине: = Дж \ xydS,= / э = Tsugyo& IS) (С) (С) Если £= 0, 9 = 0, то из Формулы (9): Т. Если в первый момент n = 0, а t = T = a, то результат、 дю кт■ ■ ■ _» —4、 sin2 греха Техас Где k = f. Таким образом, период колебаний маятника равен 7 = 4(10) Куда? Где M-масса пластины, 5-площадь
пластины, а dS-площадь основания. Консолидация распространена по всей пластине. Эллипсоид инерции в определенной точке твердого тела-это геометрический локус точки на расстоянии от этой точки до следующей. Расстояние. ВХ. Отрезок OD строится вдоль оси L, проходящей через заданную точку O, в связи с чем определяется момент инерции Сплошной (рис. 131).J с уравнением инертного эллипсоида Форма твердого тела в заданной точке ^ / ^ Т + −2 l2Xzx-2 txvxy-Джей、 ^Где x, y и z-текущие координаты точки на поверхности эллипсоида. Через любую точку твердого тела можно нарисовать луч оси L и построить соответствующий эллипсоид инерции. Рисунок I3J. если оси x, y И если мы направим z вдоль оси эллипсоида инерции, то уравнение эллипсоида примет канонический вид. То есть
центробежный момент инерции исчезает: Ось эллипсоида в определенной точке твердого тела называется принципом инерции axis. So, каждая точка твердого тела имеет 3 основные оси инерции, которые являются осями соответствующих эллипсоидов инерции. Если ось декартовых координат направлена вдоль оси эллипса инерции в заданной точке твердого тела, то есть вдоль оси инерции, то 1уг =!2X = lxv = 0, в этом случае мы получаем следующее уравнение для момента инерции твердой оси L: Ил = 1Х cos1 а -} -] для cos4 п Яш потому что 2 г, потому что, потому что Джи, потому что мне это направление Косинус оси л. Ось, которая не проходит через центр тяжести твердого тела, является главной осью только в 1 точке.
То есть ось-это ось эллипсоида инерции, с которой эта точка и ее центр совпадают. Таким образом, главной осью z точки O является ось эллипсоида инерции с центром 15 O, тогда как остальные точки имеют центр инерции эллипсоидов, которые находятся на оси z (например, O и O), а ось z не находится на оси 132 эллипсоида (рисунок). Если ось x и ось y, проходящие через точку O, не являются эллипсоидальными осями, если только 1×0 или 1 из осей является главной осью инерции в определенной точке твердого тел
а, то исчезают только 2 центробежных момента инерции вокруг оси, из которых 1 является главной осью инерции. Например, если z-главная ось инерции точки O, то Ilzy = 0 (заметим, что оси x и y проходят через точку O и образуют ортогональную систему осей координат вместе с осью z). Инерционный шпиндель, проходящий через центр тяжести твердого тела, называется инерционным шпинделем. 1 12.Я буду петь в любое время. Если твердое тело имеет материально-симметричную плоскость, то ось, перпендикулярная этой плоскости, будет главной на пересечении с плоскостью. Если твердое тело имеет материальную ось симметрии, то это главная ось инерции твердого тела. При решении задачи необходимо использовать формулу, содержащую центробежный момент инерции твердого тела (например, задача определения давления
вращающегося твердого тела на вращающуюся ось (X,§ 3), Задача удара об объект, вращающийся вокруг неподвижной оси (XII), § 1), задача динамики твердого тела, вращающегося вокруг неподвижной точки (X, 8), направление оси следует выбирать специально. Для этого нужно выяснить, имеет ли твердое тело ось симметрии материала или плоскость симметрии материала. Если твердое тело имеет материальную симметричную ось, то 1 из осей должна быть ориентирована в этом направлении
Ось инерции. Если твердое тело имеет плоскость симметрии материала, то 1 из осей координат должна быть направлена перпендикулярно плоскости симметрии материала. Эта координатная ось является главной осью инерции твердого тела на пересечении с плоскостью симметрии материала. Если в определенной точке твердого тела имеется главная ось инерции, то 2 центробежных момента инерции относительно оси (1 из которых является главной осью инерции) будут равны нулю, и только 3-й ненулевой момент центробежной инерции будет равен нулю. calculated. So, если ось z ориентирована вдоль главной оси инерции, то это будет I2X = I2Y = 0 и вычислить только 1XG. при расчете
центробежного момента инерции, например / g, иногда полезно вращать оси x и y. Если оси вращения a’j и j ’ являются главной осью, а для них известны твердые оси момента инерции, т. е. lXt и/, h, то искомый центробежный момент инерции является функцией, поэтому рекомендуется использовать этот прием в случае величины rex JXl и/,. это хорошо. Чтобы определить уравнение эллипсоида на кончике твердого тела, нужно сделать следующее: 1) Выберите координатные оси и возьмите начало координат в этой точке. Если
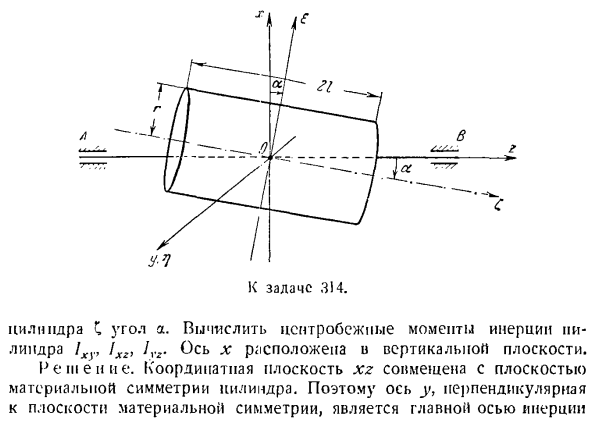
положение инерциальной главной оси может быть легко определено, поскольку плоскость или ось симметрии материала присутствуют в твердом теле, координатная ось должна быть направлена вдоль инерциальной главной оси. 2) вычислить момент инерции 1X> / y.) D и твердый центробежный момент инерции \ xy, \ xr> yy \ 3) Определите уравнение эллипсоида инерции по формуле — И-Л-У-г-2!uyz-2Lxzx-2/, LU = 1- Задача 312.На этом рисунке показана схема коленчатого вала 4-цилиндрового двигателя внутреннего сгорания. Колено А и/: находятся на горизонтальной плоскости yz. Локти B и D
находятся в вертикальной плоскости xz. Вычислите центробежный момент инерции коленчатого вала/хуу1Х2.И А, В,/, и точки D, чтобы сконцентрироваться на массу, и тА=ті=тг= = рнд =т, чтобы рассмотреть. Размеры показаны на рисунке. Решение. Определение центробежного момента инерции твердых тел дает: п п п п п Если вы распределите сумму на 4 точки массы tA, tfh tE и mD, вы получите: л !Г * = г; » Ж*=, naUa2a +! ч-я = ДС ’2А (- Б)-У ти (-2 а) 2а =-12 / наа *-4 М ^’ 1 =-\ Сипа \ н к = I ■ фщ Да. б — Л. 4г. Г Я 2а Д / * mDXDZD = К выпуску
312. 2 mkxkzk = mAXAZA + mftxnznt-mEXEZi Ко мне. =(- 2а) 2а-п- / я ^ ба (- l2a)= — 4тн ^ АР-12wDa * = — 16Р? ИА2 (вспомнить= ХД = хе = 0 и ма = // ж = Т = МД = м). И k,/ = Jxz = — \ o что *и / «=О. Отметим, что центр тяжести коленчатого вала находится на оси вращения G, в отличие от Xg и пули, за счет вращения центробежного момента инерции. Задача 313.Вычислите центробежный момент инерции однородной пластины RLV массой P, JKyt fxz и ly2.Нога прямоугольного равнобедренного треугольника RLA — это a. координатные оси
показаны на рисунке. Решение. Ось x, перпендикулярная плоскости симметрии материала пластины, равна ke O. Главная ось инерции в относительной точке инерции 1 из них является главной осью инерции, ось равна нулю, то есть, 1 ху = я, Х2 = 0. Приступим к расчету центробежного момента инерции Iyz. 1n = \ Y 2 dm, Вт) Где dm = *(dy dz>и y-плотность пластины. И так оно и есть.、 — в / ,, = 7 ^ yzdydz = я Г ды ^ здз = я [Г(А-вы ды = Про футы 0 один = Я)^ Г〜+ /) И затем
Потому что\ y = M-) Задача 314.Прямой, равномерный цилиндр с радиусом основания равным весу P, длиной 2/, r установлен на горизонтальной оси r через центр тяжести O. ось z сформирована вместе с осью. Цилиндр C угол a. вычислить центробежный момент инерции цилиндров 1hu, 1hg, 1Ug. ось x находится в вертикальной плоскости. Решение. Координатная плоскость xz совмещена с плоскостью симметрии материала цилиндра. Поэтому ось Y, перпендикулярная плоскости симметрии материала, является
главной осью инерции Является эллиптическим интегралом типа 1.Коррупция 1-sin2 * sin2 и Если вы консолидируете каждый термин в строке, это выглядит следующим образом: (грех 24 9 грех1 в Подставляя полученное значение K в уравнение (10), получаем искомую формулу для периода колебаний маятника. (11) = 2 + грех +£грех*£…)、 То есть колебание маятника с конечной угловой амплитудой не обладает изохронным свойством-его период зависит от угловой амплитуды колебания а. предполагая, что a-малая
величина и игнорирует члены разложения в уравнении (11), включая порядок a и более 2, получим приближенную формулу (7). = 02) Если угловая ширина колебаний колебаний равна% −20°, то период колебаний, рассчитанный по формуле (11) или более неустойчивой формуле(10), больше периода колебаний маятника, который определяется приближенной формулой (2), всего 0,8% а = 601, соответственно, уже 3,6%.
Пересечение цилиндра с этой плоскостью, то есть точка O. As вы знаете, что центробежный момент инерции твердого тела относительно оси равен пуле, 1 являющейся основной инерционной axis. So … / , » = / ,,, =о. Осталось рассчитать момент центробежной инерции н 2 mkXk * к-о) k = I введем новую систему осей так, чтобы ось z совпадала с осью y, а ось 5 и ось C вращались на угол a относительно оси x и оси Z. По часовой стрелке. Формула преобразования координат для вращения с углом a в направлении против часовой стрелки выглядит следующим образом. З = \ потому
что я грех и X =(.грех -} — $ потому что.(2) В этой задаче вращение через угол a завершается по часовой стрелке, заменяя A в уравнении (2) на-a, так что это выглядит следующим образом: З = = С потому что А-Ф-Е Син А и Х = — с грехом, а-j-Е потому что. (3) Подставляя значения z и x из уравнения (3) в (I): Н. Н. Н. 1xr = ^ mkxkzk = Y] / 7 / ft (Cftcoso.+ ^ Sina) В (- С ^ СЛН а + соз а)= л = я к-я L I / 1 = — Грех, а потому что + ко $ * это-грех * А / ч ^^ — л к = I / Г = Я = я / 2Р П В Т * 2а / V Т * В и Грех, потому что М&К= —2—(^-2-1 «т. фут = и к ^ 1 м * я Н. Н. Н. + cos 2a \ x4C „6,= [2“ *(C-I — b) −2 a + + К-Л К = 1 К С = * я — Ф / wcos2a. (4 )) Ось перпендикулярна плоскости симметрии материала цилиндра
и поэтому является главной осью инерции в точке O. So, / ce = 0, и выражение(4) принимает вид: вы можете найти дополнительную информацию здесь.) к = я-я ’Hack, как C -} — m, где 2 = rfjk, где d * c-расстояние от материальной точки LI до оси C, а C is^ — расстояние от материала Томк до оси Н. Н. Н. Х Т + рил) = tnkdlc= к-я-к » = я л п C (C + rtl)=£mtdi = f:. 1 Л-Я Где выражение (5) принимает вид: Для круглых и равномерных цилиндров Пр, р(р,/. / с = м-и/ Е = — я + 1р! Подставляя
знак/ s и/ s выражения (6), получаем, наконец.: Р / Г2 = 2 ^(t_z) грех 2а Задача 315.Напишите уравнение эллипсоида инерции, построенного на центроиде однородного круглого цилиндра массой m Базовый радиус равен высоте g 11 координатные оси показаны на рисунке. Начало координат O совпадает с положением центра масс цилиндра. Решение. Уравнение эллипсоида инерции в заданной точке твердого тела、 + / , / + ч? −2 / угу *〜〜 — 21хуху = . г<- «• Как известно, для круглого цилиндра 1l = 1y =и / 2 =.С если ось x, y, z является главной осью инерции цилиндра, то 1ug = \ xg = 1xu =
0.Уравнение эллипсоида инерции центра тяжести цилиндра выглядит следующим образом: Джей Джей 1 Ноль / / Год х / 7 — ^ — ь Цели 315 Ось эллипсоида инерции равна Один И затем — г и М ’ а = 0 = Проблема 316.In отношение радиуса основания однородного круглого конуса к его высоте h, эллипсоид O, состоящий из Верхнего O конуса, становится сферой. Оси показаны на рисунке(см. рисунок в задаче 29). Решение. Напишите уравнение эллипса инерции однородного круглого конуса для его вершины O. для этого уравнение эллипса инерции + 1yUg-1— 21uyaug-V2Xzx-2lxvxy = I 3 Г2 3 О) мы должны заменить. Что взять: −5 *(/. ’Y4) x * +» M (и * — й го = 1•
В результате полуоси эллипса инерции конуса в точке 0 1, 1 т / по » а=Т7з, и€=тУт- г * м («+ГТ) Поверхность эллипсоида, А = B = C, то есть Юм [^ + r4L Задача 317.Если мы знаем, что момент инерции твердого тела относительно этой оси минимален, мы определяем положение точки в твердом геле и направление оси, проходящей через эту точку. point. It предполагается, что эллипсоид инерции всех точек твердого тела задан. Религия: применяя теорему шейпера, если
существует система параллельных осей, то момент инерции твердого тела будет минимальным относительно оси, проходящей через центр инерции твердого тела C. задача 317 остается нерешенной. Возьмите направление проходящей оси В этот момент. Создает эллипсоид инерции вокруг точки C. Расстояние от центра эллипсоида по определению эллипсоида инерции До определенной точки на его поверхности равна CD -, где/、- В ЛЛ Солидный момент инерции
относительно центра эллипсоида и естественно по проходящей через точку на его поверхности. Чтобы свести к минимуму момент инерции, расстояние CD должен быть максимальным. В результате, нужные ось L проходит через центр инерции с твердого тела, вдоль максимальной оси диск эллипсоид инерции, построенный на этом выводе.
3 в случае сохранения углового момента массы точки. Если векторная сумма моментов около неподвижных центров всех сил, приложенных к точке массы, равна пуле, то угловой момент точки массы относительно того же центра постоянен, то есть она постоянна. н если mo (Fk)= 0, то/ o является постоянным. тебя * Аналогично, если сумма моментов силы, приложенных к материальной точке относительно оси, равна пуле, то угловой
момент этой точки относительно той же оси постоянен •мой пример、 н U. Если mx (Fk)= 0, то 1X-константа. Я При изучении движения точки массы и действия центральной силы удобно использовать эти частные случаи теоремы об изменении углового момента точки массы. Задача использования закона сохранения углового момента массы может быть решена путем соблюдения следующей последовательности действий: 1) Выберите center. In в связи с этим необходимо применить теорему об изменении
углового момента важной точки(если точка движется под действием силы центра, то центр силы должен быть расположен). 2) на рисунке нарисуйте все заданные силы и силу реакции связывания, приложенные к важным точкам. 3) определить вектор импульса точки массы и найти момент импульса этой точки относительно центра. Л) так как мы применили теорему об изменении углового момента материальной точки к центру и подтвердили, что сумма моментов всех сил относительно центра равна нулю、 Момент
импульса в начальном и конечном положении материальной точки:/ 2o =ЛEEE1C-й из уравнения определим искомое значение. В некоторых задачах необходимо использовать эту теорему относительно 1 из осей координат. Задача 285.Материальная точка движется под действием центральной точки F, и ее линия действия всегда проходит через точку O. Задача 2×5 к. Скорость точки ниг от Л12 положение, чехол А7 、 ОМ Скорость v 4M’, секунды,
сформированный угол Скорость Vz на линии действия силы, а = 60°(см. рисунок).Вес точки M игнорируется. Решение. Применим теорему к изменению углового момента материальной точки относительно оси r через точку O, перпендикулярную плоскости фигуры (эта ось на рисунке не показана). н К Момент, потому что только сила F приложена к точке массы н Равна пуле относительно оси На самом деле, lz-это constant. In другими словами, лиз-это I. It равен 2z. момент
импульса материальной точки в положении My относительно оси z 1 \ r = / iVfOMj. момент импульса массы точки Mt, расположенной относительно оси z Лл: = mvji = МВ± * ом.- грех а. / 1р = тогда МВ \ * ом = МВ ^ * ом $ грех, wherece в ^ = ом、 = r, 1yyy — ^ — •после замены числа、 1 ом » Си Джей v. i = 6, 2 мс 4. теорема об изменении главного момента импульса в материальной точечной системе. Производная по времени от главного момента импульса материальной системы относительно неподвижного центра равна сумме моментов всех
внешних сил системы относительно одного и того же центра. ^ = М-М0 (ФК). (Это лшшш k = I (Заметим, что формулировка этой теоремы даже не включает внутренние силы системы при изменении главного вектора импульса системы материальной точки, как в теореме о движении центра инерции. Форма той же теоремы, записанной на оси декартовых координат, выглядит следующим образом: L = I 1 * = I C> ’ — \в случае сохранения основного момента импульса материальной точечной системы. Если векторная сумма моментов всех внешних сил системы относительно неподвижного центра системы равна нулю, то основной момент импульса системы относительно этого же центра постоянен. н Х ТП (к)= 0.к-1 Тогда
горный век L0 постоянен. Аналогично, если сумма моментов всех внешних сил системы относительно неподвижной оси равна пуле, то основной момент суммы Движение системы по одной и той же оси постоянно. Например н если / rcJC (/JJ)= 0, то Lx является константой. Ко мне. При рассмотрении движения материальной системы, включающей движущуюся среду, вращающуюся вокруг этой оси, целесообразно рассмотреть теорему об изменении главного момента импульса системы материальных точек относительно неподвижной оси. Если сумма моментов всех внешних сил системы относительно
оси равна нулю, то можно получить отношение между массой масс, их скоростью и угловой скоростью вращения движущейся среды. Задачу целесообразно решать с использованием теоремы о сохранении основных моментов импульса в следующем порядке. 1) отправьте 1 из координатных осей вдоль фиксированной оси вращения и выберите координатные оси. 2) вся внешняя сила системы показана на рисунке. 3) Напишите теорему об изменении главного момента импульса материальной точечной системы
потому что(X, в)= 7Т-я, потому что (> ’ , / 0)= — ф -, потому что(З. Ы п0)= — если-. * «о! я о я я о• Момент массы для оси декартовой координаты задается формулой: ЛК = М(Г 2-2$), и ly = м(на ZX-ХС), ЛЗ = м(х $ — э)、 Где XY уу Z-это координата материальной точки в системе координат с центром o своим происхождением. x.}>, где I-проекция скорости точки на ось оси. Главным моментом импульса системы
материальных точек для центра О Ло (кинетический момент) является векторная сумма моментов импульса для того же центра материальных точек системы. Н. Н. Н. Ло = Йи л * о = c(РК х / Ил) k = 1 k = I 4) момент внешней силы системы относительно оси указывает на то, что сумма nsec равна нулю. 5) вычислить и уравнять главные моменты импульса системы материальных точек относительно начальной и оси коня» > Н. Н. Н. 5-й момент времени: C2 =£lik2 и = Y] k = I k | в) решите уравнение, чтобы определить желаемое значение.
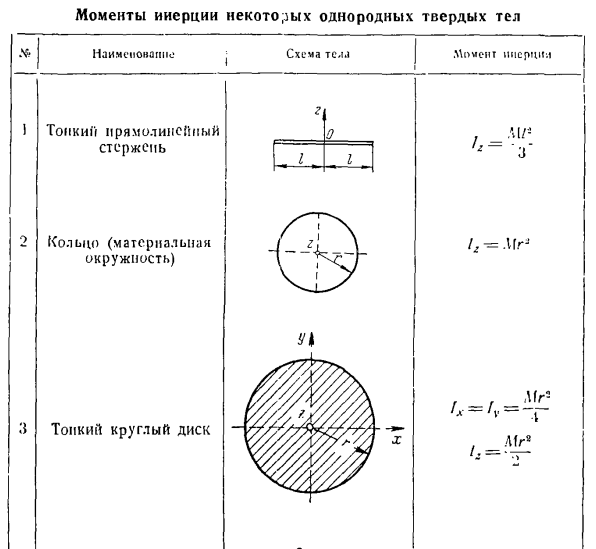
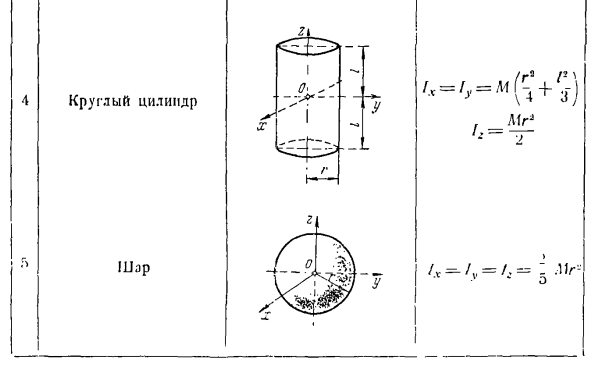
Основной момент движения твердого тела, вращающегося вокруг неподвижной оси относительно оси вращения, равен произведению проекции момента инерции твердого тела относительно этой оси на скорость вращения. Lz = Извз. Момент инерции твердого тела относительно оси равен сумме произведений массы материальных точек, составляющих твердое тело, на 2-ю степень расстояния до оси. н к = 1 Момент инерции твердого тела вокруг оси характеризует массовое распределение материальных точек вокру
г этой оси. Момент инерции всегда положительный. Момент и peri и kgm-sec1 единицы измерения. При непрерывном распределении массы материальной точки в твердом теле момент инерции определяется по следующей формуле / , = \ r2dm. L1) Для однородного твердого тела существуют следующие условия: Где M-масса твердого тела, V-объем твердого тела, dV-объемный элемент. Теорема Штейнера о соотношении моментов инерции твердого геля на параллельной оси формулируется следующим образом: момент инерции твердого тела на оси-это сумма массового произведения массы твердого тела в порядке 2 мощности момента инерции и расстояния между параллельными осями геля), т. е. ФН = Ф、 Ради
ус инерции твердого тела относительно оси р — это величина, в которой произведение квадрата с массой твердого тела равно моменту инерции твердого тела относительно геля вдоль этой оси. О Итак, для шара I,= ^ Mg ’: = =11р*, из которых Р = 0,63 г. В процессе решения задачи, когда необходимо рассчитать момент инерции твердого тела вокруг своей оси. Если он не проходит через центр тяжести, проведите параллельную ось через центр тяжести твердого тела и примените теорему Штайнера (в этом случае момент инерци
и твердого тела относительно оси через центр тяжести, масса твердого тела и расстояние между параллельными осями должны быть известны). Если нам нужно вычислить момент инерции материальной системы, состоящей из нескольких твердых тел, и мы знаем момент инерции каждого отдельно взятого твердого тела, то момент инерции системы для одной оси определяется как сумма моментов инерции всех твердых тел, входящих в систему для одной и той же оси. При расчете инерции однородного плана вокруг
определенной оси на виде в плане выбирается базовая область, которая известна или легко вычисляется для инерции вокруг соответствующей оси. Затем, суммируя моменты инерции всех базовых областей, определяют искомый момент инерции однородного вида в плане. Когда вы вычисляете момент инерции однородного трехмерного твердого тела вокруг определенной оси, оно разделяется на твердые тела. Такой фундаментальный объем можно легко определить, известен ли момент инерции для соответствующей оси. Затем, суммируя момент инерции всех основных объемов, вычисляется искомый момент инерции однородного твердого тела. Проблема 286.Вычислите момент инерции и радиус инерции кругло
го диска с массой P и радиусом r, лежащего в плоскости, равной 4 минутам радиуса и равной 1 для оси r, удаленной от центра тяжести c диска. Решение. Нарисуйте ось Lc Голы: 286 Центр тяжести диска параллелен оси L. As я вижу, что момент инерции однородного кругового диска равен Мг * Если ось проходит вдоль 1 ее диаметра и применить теорему Штайнера, то можно увидеть следующее: дл СН. С и Т) −4. 16-1 пример ’ П Используйте формулу I = y pj для определения радиуса инерции P диска относительно оси L. Вы.} Четыре планирование семьи./ = От W > h Какой-то момент инерции Мехпримеси исртсни момент ТК / схемы ИЖ Ваше имя Тонкая прямая палочка г Да. 。 1-1 / _l, за [/ ’ Кольцо (материальный круг) Мэдди круглый диск Я= / ’Х -’ в— На g8
Круглый цилиндр Мяч Задача 287.Самка имеет твердый момент инерции и отделена друг от друга на расстоянии d относительно 2 параллельных осей u. / , −2.Центр тяжести твердого тела Масса M находится между осями F ’ yx и y.Какая Ось Что находится вблизи центра тяжести твердого тела и сколько? Решение. i-я ось uh и u. проведите усы оси, параллельной оси 2, через центр тяжести c твердого тела. Применяя теорему Штайнера 2 раза, вы можете увидеть следующее: ХТ = / МК + Лей(я) ИИ = лицей- \ — МД . (2) По условию/, -, dxy> db, то есть потому, что ось близка к центроиду C. Если вычесть уравнение (1) из уравнения (2), то получится: привет- ’ Λ= ^(д \ — д) = М(ДХ + д) (、-<РФ/、); ‘=°> 05 + 102 = 102> 05′ 9.8! 2 я 9.81 Момент инерции вала пренебрежимо мал, так как он составляет
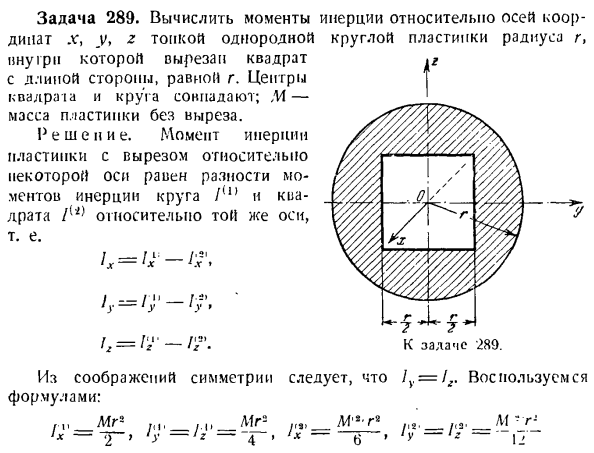
всего 0,05% от момента инерции маховика. Выпуск 289.In равномерная равномерная топка, координатные оси. вычислите момент инерции относительно v, y, r. вырежьте квадрат, сторона которого равна r по длине. Центр квадрата и круга совпадают. M-масса пластины без вырезов. Определение: момент инерции пластины с вырезом для оси равен разнице в моменте инерции между окружностью/ (.) и квадратом I [i) для одной и той же оси. / — /Я- Круглая пластина с радиусом r、 г Переходим к выпуску 280. х-1Х 1Х」 Я — / И! — > ’)- 1У’ У ’ Из рассмотрения симметрии следует, что/ y=/,.Используйте следующую формулу: М ’ * — Г / 1 «_lvu 7(1’ / −1» _ ’vu l<> _ ’ / ’2′ / <3- _ _ ’ x — rc-Ji-у-12 — d «’x-П» ’ у-г—. 、 В-г- Мг- МГ- (Ошибочно полагать L0 = rc X, так как импульс главного вектора
движения относительно центра обычно не равен импульсу всех материальных точек системы относительно одного и того же центра.) Основной момент импульса материальной точечной системы относительно оси декартовой координаты определяется по формуле. п п п п п ^ x ’ — ^ J Kx * i’y — ^ J by * = 2 кг * k = — = I h = 1 k = 1 Сравнивая соответствующие формулы, легко проследить полное сходство понятия момента силы в статике и понятия момента движения в механике. М0 (Ф)= rXF> 1о = ГХ М *>и т. д. 2°.Теорема об изменении углового момента точки масс. Производная по времени вектора момента импульса точки массы для неподвижного центра равна векторной сумме моментов для одного и того же центра всех сил, приложенных к точке массы. МО(Ф>). ДТ З =] Г../ о) мл М. \ Здесь
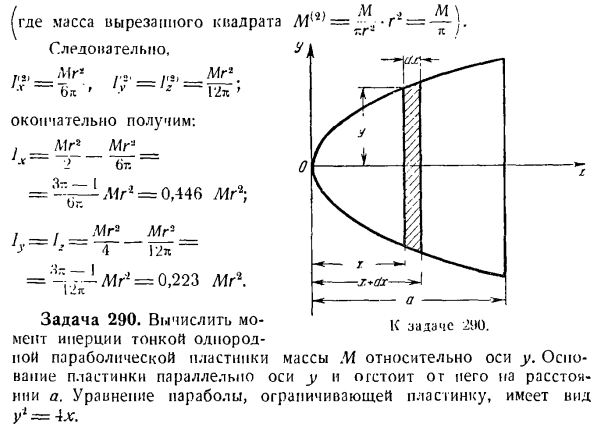
масса отрезанного квадрата Mk’= -.- р.- = T. G. » Я есть Так… Ш. к проблеме. лf3, / мг » / * 2•_ / гы » ^^、 ’г’—、 Один Окончательно получаем: _ Л Г * _ 1 (младший. = Г * = 0.446 МР2; Я am_/. Г-н. Г-н- __ −4-12 * ~~ = — \ТК-г * = 0.223 МР2. Задача 290.вычислите момент инерции тонкой, однородной параболы относительно оси Y. Основание пластины расположено параллельно оси y и в стороне от оси Y. Форма параболического уравнения, окружающего пластину, равна y * = 4x. Решение. На пластине нарисуйте 2 прямые линии, параллельные оси
y, разделенные расстоянием x и x-dx. Рассчитайте момент инерции вокруг оси масс площадки. Эти линии и парабола пластины очерчены тенями: dlv = xidm, где базовая масса области штриховки пластины равна dm = f ds. Где y-плотность пластины, (/5-площадь заштрихованной области, ds = 2y dx. Так, ДМ = 2yydx и DLV = 2yxlydx. Поскольку, по предположению, У2 = 4л, т. е. г = 2 г х, то Д / Г = 4 Форекс * х ДХ. момент инерции пластины относительно оси Y / г = ^ выд 4-ПК-в-xdx = \ ты: «Я. 。 (. Си Ри Масса пластины равна AJ = 7.Поскольку она равна S, площадь пластины равна 2й ДХ = 4 ^ г / xdx = У а, то в = г г в. (Обо мне Учитывая формулу для массы m пластины, опишем искомый момент инерции в виде/. = Met1. Задача 291. Вычислите момент инерции вокруг оси X, y, g однородного круглого конуса массы MD.
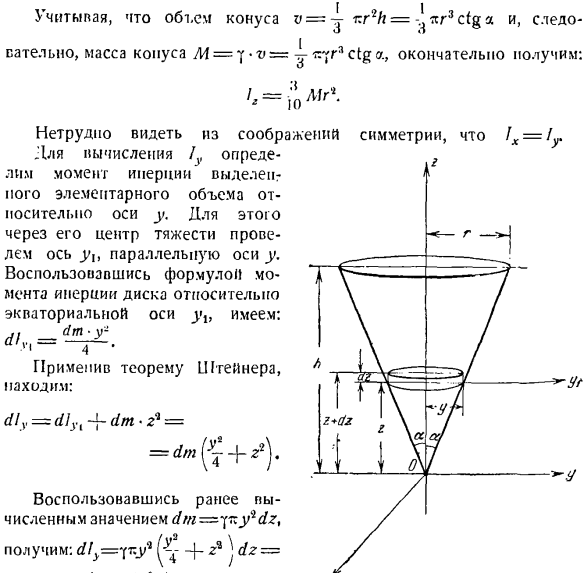
Высота h и радиус основания g (см. Рисунок). Решение. разрежьте конус плоскостью, параллельной плоскости xy, и с интервалами расстояния z и z + dz. Вычислите момент инерции этих плоскостей и массу базового объема, окруженного сторонами конуса. Разница в объеме тела определяется как объем цилиндра с базовым радиусом y и высотой dz, т. е. dv = r, yidz. So, масса выбранного элемента объема равна dm -=. = — ДВ = ^ Ку-ДЗ, где F-плотность конуса. Момент инерции основного объема педераста для оси
Объем конуса равен v = 4-gU2U=~!Учитывая, что jag3 является cfg a, следовательно、 О, да. Действительно, масса конуса= = y ir * r3ctga, которая в итоге выглядит так: И затем = 10 л, г• Из рассмотрения симметрии легко увидеть, что 1X = 1.Определите назначенный момент инерции для расчета 1y? Пого базовый объем для y-axis. To сделайте это, нарисуйте ось y параллельно оси y через ее центр тяжести. Используя уравнение момента инерции диска для Экваториальной оси y1y, можно увидеть: а я-4• Применяя теорему Штайнера, вы можете увидеть: выд = dlyi + ДНТ’2 * = = * .(?+ 4 Ранее
рассчитанное значение dm = * [izy * dz、 Вам: выд = интернет: ут-ф-г : ДЗ- K задача 291 в ’ 6 \ 1 4 j г = зто а). расчет момента инерции конуса вокруг оси Y () О » Масса конуса равна M = .предположим, что она равна j — \ tk и J * = tan Падуб: Поскольку X = 1y, это, наконец, выглядит так: Задача 292.Вычислите главный момент импульса относительно естественной степени вращения массы M и радиуса R лскке, который установлен эксцентрично на оси вращения
и вращается с угловой скоростью W. Плоскость диска перпендикулярна оси вращения. Эксцентриситет будет равен половине радиуса. Решение. Направим координатные оси r вдоль оси вращения Основной импульс движения твердого тела относительно оси вращения равен Lz = lzw. Где 1g-момент инерции твердого тела, а вращения вообще нет. для вычисления lz используйте Stei georem Ручка. Диск, который мысленно проходит центр тяжести C: — ос
ь, параллельная оси z: К выпуску ’ 292. 1р = 1С + м [{ Мистер -, Мистер ’3.. s = — » G — = 4 мг» Следовательно, главный момент движения рассматриваемого диска для оси вращения r равен、 Задача 293.Если человек, стоящий на идеально гладкой горизонтальной поверхности, начинает вращать руками над головой, Может ли он повернуться? Решение. Перпендикулярно неподвижной плоскости укажите ось g через центр тяжести человека и изобразите внешнюю силу,
приложенную к человеку: P-вес тела человека, а R-нормальная сила реакции плоскости(нет силы трения, так как плоскость идеально гладкая). применим теорему к изменению главного момента импульса материальной точечной системы относительно оси Z. — >•=Т » ЛП). U 1 н Поскольку внешние силы P и R находятся на оси z, Y] tns (Fl)= 0 к-1 То есть,= 0 и L являются константами. Отсюда и з R = Лиз. Поэтому главный момент импульса материальной точечной системы относительно оси z может быть сохранен. Этот человек был первым rest. So, Ltz = Q. далее, человек поднимает руку над головой,
и относительная угловая скорость ω вокруг оси z? Я начал вращаться вместе с. В этом случае тело человека начинает вращаться в одном направлении с угловой скоростью c’/’. при этом основным моментом импульса движения системы относительно оси z является Llz-L’L —.- /./ И так далее、 = /; <«;•、/。/ ■ = / ?добро пожаловать на наш сайт!、
Где fg-момент инерции руки относительно оси вращения. ztIf-момент инерции тела относительно оси вращения. г-абсолютная угловая скорость руки. Имея в виду, что руки человека выполняют сложные движения (их можно носить и носить с телом), они выглядят так: w: / = wU ’ w /’ Все нормально. Ll2 = LT + LT = 1? »* + » ? ’)/?На FM. Если ТСЖ = ТСГ и ТСГ = 0, то: / U’K»*+<«/’) + w = o、 * К проблеме ’ 293 Откуда Ноль один Уй. Я Г ’ Мне.* U) Л Р ’ +1? Знак минус указывает на то, что человек вращается вокруг оси z в направлении, противоположном вращению руки. Поэтому человек, стоящий на идеально гладкой горизонтальной поверхности, может поворачиваться вокруг оси
через центр тяжести, перпендикулярный этой плоскости. Задача 294.Днище груза расположено симметрично по бокам конуса, соединенных между собой тонкой нитью, отстоящей от красильной оси конуса на расстоянии 3 мин 1 радиуса днища конуса. Конус вращается с угловой скоростью вместе с грузом (часов).После того, как нить внезапно лопнула, груз начал тонуть, но упал в сторону конуса. Определить угловую скорость конуса в момент, когда нагрузка достигает основания конуса. Вес каждого груза в 4 раза превышает вес
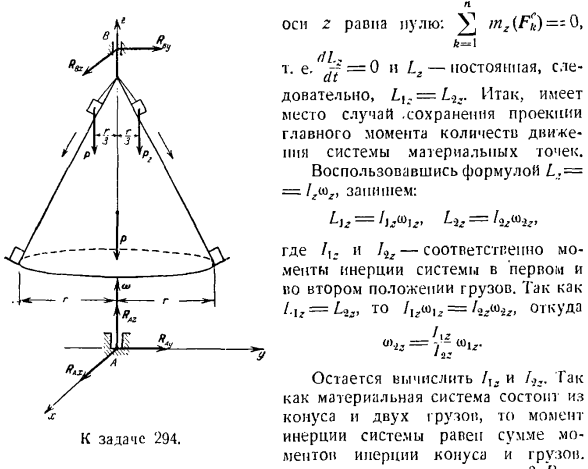
конуса. Игнорируйте сопротивление движению. Нагрузка считается точечной массой. Решение. Дно оси конуса после получения начала координат в опоре а, направьте ось z вдоль оси вращения конуса. P-длина конуса, R-радиус основания конуса. Обозначим внешние силы материальной системы, состоящей из конусов и 2 нагрузок. P-вес конуса, P {и P.-вес груза, RAx% / ?成raz, RIU, Rn «ЛП). к = \ Поскольку все внешние силы параллельны или пересекаются с осью вращения z, сумма моментов всех внешних сил равна
Форма той же теоремы, записанной на оси декартовых координат, выглядит следующим образом: н длы _ (Он Н. Н. Н. £= 2 k = I х В следующем порядке рекомендуется решить задачу, используя теорему об изменении углового момента точки масс. 1) Выберите систему координат(когда точка движется по дуге окружности, 1 ось проходит через центр окружности перпендикулярно плоскости, и вам нужно выбрать положительное направление опорного углатак что 1 \ р <р \ р = 1 * ррр, откуда И: Так как материальная система состоит
из конусов и 2 весов, то необходимо рассчитать/ 1r и Hack. In в этом случае момент инерции системы равен сумме момента инерции конуса и массы. Момент инерции конуса к оси вращения р^ — р \ Рассмотрим нагрузку как точку mass. In в соответствии с начальными и конечными условиями товара, он записывается следующим образом: 3 я 4 П / гр. _) 6Р,, _ _ 3£4Г-、 7 | * — Хы 4 4 ^ \ 3/45-г р-10 и Р 1 «4 о-5 л Если вы используете найденные значения / 1g и / 2,
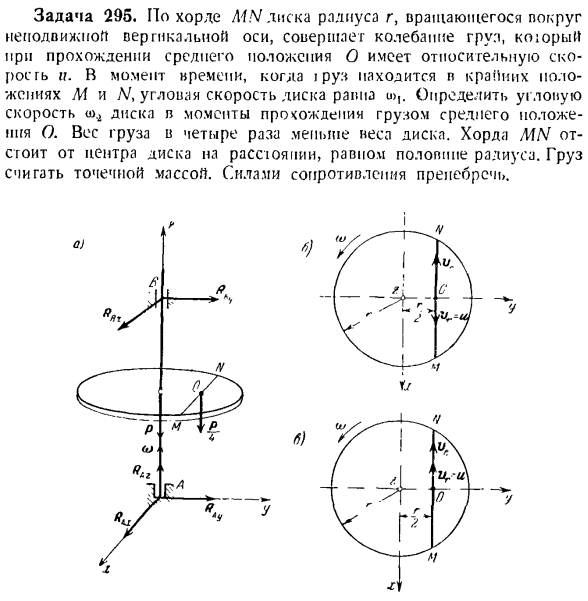
Вы получаете: Четыре Проблема 295.It вращается вокруг неподвижной вертикальной оси вдоль струны MN диска с радиусом r, что вызывает вибрацию руля r. когда I РУз находится в экстремальных положениях M и A/, угловая скорость диска равна u>.Определите угловую скорость диска в момент, когда груз проходит через промежуточное положение O. вес груза в 4 раза превышает вес диска. Код MN отстоит от центра диска на расстояние, равное половине радиуса. Рассмотрим нагрузку как точечную массу. Игнорируйте силы сопротивления. Голы 295 Решение. После выбора исходной точки в опоре A в нижней части укажите ось z вдоль оси вращения диска. Изобразим все внешние силы материала п Реал
системы, состоящей из диска и нагрузки: P-масса диска,-4-грузозахватная собака, # Ah, RBxy-составляющая несущей способности Реакция (см. рисунок А.). Применим теорему к изменению главного момента импульса материальной точечной системы на ось вращения z\ k = I Момент всех внешних сил на оси вращения северный^ Если она равна пуле, то mz (Fh)= 0, то есть= 0, а Lz-константа. л = 1 Следовательно, Llz = Liz. Поэтому основной импульс материальной точечной системы относительно оси 2 может сохраняться. Когда груз
занимает крайнее положение (M или L’), скорость относительно диска равна скорости пули, следовательно, C2 = 1 \ r (lXr, где/ \ 2-Момент инерции материальной системы, состоящей из диска и груза, положение M или/ V).、 j_ /-и J/’:?> _Pr〜 «_3 и A ’1р -р-р ^- — г’ р 4dg Р ~~£ ’ Где Iz — «момент инерции диска,/ /’ — момент инерции диска. load. So, основной момент импульса системы L \ z находится относительно оси 2 в крайнем положении нагрузки. Главным моментом импульса
системы Tsg для оси Z со средним положением нагрузки является сумма моментов импульса нагрузки для той же оси LY, что и моментов импульса Uz ’ диска: ТСГ = У +(2) У нас есть: Щ-1г11Щг = y < 3 В дополнение к этому、 v’LJ = — [- v ’ rV — ^ w,, — I-и Где v’a-абсолютная скорость груза и масса груза. Так как груз совершает сложные движения (относительно диска, переносимого вместе с диском), то в проекции на ось Т применим теорему сложения скоростей точки<va = ve-\ — vr (см. Рисунки B и b), которая расположена вдоль MN.、 Результат、
Подставляя СХ из вида (4) (3) в Формулу (2), Находим главный момент импульса системы для 2 осей, включая среднее положение нагрузки. 1 _ _ 7 дней: _;> r-i P / T,\ T — Я Ч *—2 э * — р ^ 2 ″ Д 11 ХЈ-2″ Иначе говоря 9 вечера. РГ так как г= = яя>, используйте выражения (I) и (5), чтобы получить: 3 П * 9 П 4, ПГМ-•—р(о, -=,.-Г Ж), — 4 — — г, — м、 4£16 г 8 г 1 ′ Откуда 4 2 т Поэтому, если нагрузка колеблется вдоль струны MN диска, то скорость вращения диска изменяется за счет постоянства
основного момента импульса материальной точечной системы к оси вращения. Момент, когда груз проходит через среднее положение, проекция угловой скорости диска на ось z 4 2 и Если направление вращения диска совпадает с относительным перемещением груза(фиг. 4 часа < ^ = ° −3 > из-з、 Для противоположного направления относительного движения груза и вращения диска(рис.
Б) и= — и, т. е. 4, 2 и 6°.Дифференциальные уравнения для вращения твердого тела вокруг неподвижной оси. Дифференциальное уравнение для вращения твердого тела вокруг неподвижного естественного ПО имеет вид、 Я Где<p-угол поворота твердого тела,/, — момент инерции твердого тела относительно оси вращения, а tj (fj) — момент L-й внешней силы относительно оси Z. Из сравнения этого дифференциального уравнения с теоремой о движении кесарева
от инерции материальной системы: КТМ =£К ~~ При использовании для решения задачи о поступательном движении твердого тела масса твердого тела для поступательного движения M и момент инерции твердого тела для вращения вокруг неподвижной оси z\ 2 имеют одно и то же значение: масса At является мерой инерции твердого тела для поступательного движения; момент инерции G является инертной мерой твердого тела, вращающегося вокруг неподвижного основания. Используя дифференциальные уравнения для вращения твердого
тела вокруг неподвижной оси, можно решать как прямые, так и обратные задачи динамики. По отношению к закону вращения оси вращения и твердого тела в прямой материи в данный момент инерции твердого тела I? = / (0 определяет первичный момент, связанный с естественным po этой внешней силы, приложенной к твердому телу. В обратной задаче rjo уравнение вращения заданного твердого тела= /(/).в этом случае необходимо указать начальные условия движения. То есть, положение и угловая скорость твердого тела в первый момент. Четыре Т = 0 <? = <?0. 9 = рН Поскольку необходимо интегрировать дифференциальные уравнения для вращения твердого тела вокруг неподвижной оси, решение обратной задачи часто сопровождается большими
трудностями. Момент внешней силы относительно оси вращения — это не только время или время, но и угол поворота o и угловая скорость и трехмерность, то есть, в’ )• Немного обо мне Если момент внешней силы постоянен или является функцией только времени, то задача легко решается. Сплошные Ц. задача о динамике вращения вокруг та не является необходимой и должна решаться следующим последовательным т. 1) Выберите ось декартовых координат и укажите 1 из них (ось z), но это ось вращения твердого тела. 2) относится ко всем внешним силам, приложенным к твердому телу. 3) вычислить сумму момента силы, приложенной к массе
по отношению к координатным осям. 4) Нарисуйте вектор импульса точки массы, запишите выражение ее моментов относительно осей координат и выведите производные от них с помощью надбавки. 5) подставляет результат вычисления 2 предыдущих точек решения задачи уравнения теоремы об изменении углового момента материальной точки. 6) решите прямую или обратную задачу динамики точек в соответствии с условиями. 4) решение задачи может быть осуществлено после I) путем обхода 2) и 3). Выпуск 284.Найти законы и периоды колебаний математического маятника, где длина нити равна/.в первый момент маятник был
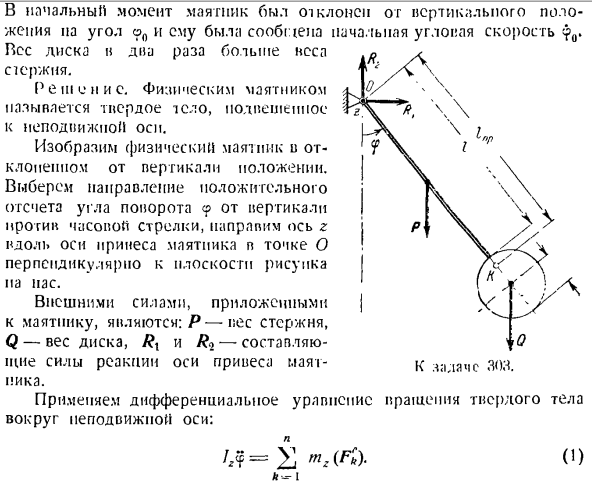
проинформирован о начальной угловой скорости толчком, поскольку нить занимала вертикальное положение. Решение. Математический маятник подвешен на невесомой, растягиваемой струне от неподвижной оси и является важной точкой движения в вертикальной плоскости. На рисунке маятник изображен в положении, которое отклоняется только от вертикального угла cf.
Направление положительного опорного угла * o показано на рисунке. Маятник перпендикулярен плоскости фигуры и качается вокруг оси z, проходящей через точку O веса. Локус массы представляет собой дугу окружности на перпендикулярной поверхности с радиусом / центрированным на о.
3) вычислить сумму моментов всех внешних сил относительно оси н Вращение тг Ко мне. 4) записывается дифференциальное уравнение для вращения твердого тела вокруг неподвижной оси ’/ ? = В(*)、 В ней подставляют величину момента инерции 12 твердого тела относительно оси вращения, представляющую собой сумму моментов всех внешних сил, и, в зависимости от условий, определяют задачу прямо или косвенно. Задача 296.Твердое тело вращается вокруг неподвижной оси под действием силы сдвига, приложенной к нему. Чему равен главный момент внешней силы относительно оси
вращения для того, чтобы вращать твердое тело: а) равномерное, б)одинаково переменное? Решение. укажите ось z вдоль оси вращения твердого тела и напишите дифференциальное уравнение для вращения твердого тела вокруг неподвижной оси. // ?= 2 TLP>、 k = I а)для равномерного вращения, угловая скорость$твердого тела постоянна. Следовательно,£ = 0 и £МЗ (фдж) = 0 Л = Г я 1. e. главный момент внешней силы по отношению к оси вращения равен нулю. б)в случае одинаково переменного вращения угловое ускорение тела С
СР является постоянным、 н Г)М..(F’b)= const, k = i То есть основной момент внешней силы относительно оси вращения, но он более томный. Задача 297.Под действием диска с радиусом 20 кг и радиусом 10 см, вращающегося вокруг неподвижной оси, определить величину крутящего момента///по закону о = 4т1. Решение. Укажите на ось 2 вдоль оси вращения диска. Дифференциальные уравнения вращения диска вокруг неподвижного! формат оси z: н // ?=£к = 1 Внешняя с
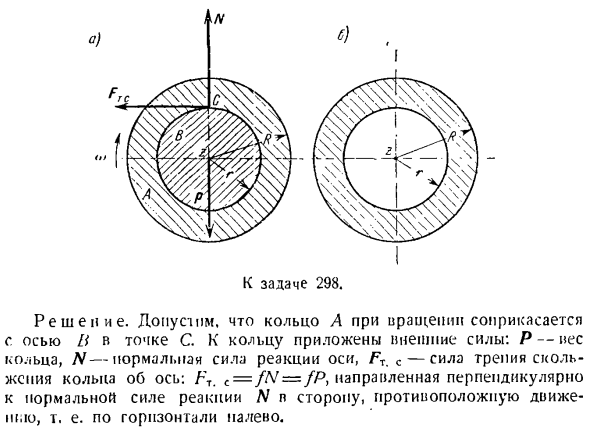
ила приложена к диску и своему axis. It это пара сил, которые должны определять силу реакции опоры, вес диска и момент. Так как момент силы опорной реакции и масса диска относительно его оси вращения 2 равна пуле, то сумма моментов всех внешних сил равна искомому моменту пары сил относительно оси вращения Z. So … группы PG2 = / / Ф Момент инерции диска относительно оси вращения z имеет следующий вид: Pr — ’ 20.0,я, ЖВ «/ ГУ 0 я Тогда необходимый вращающий момент мг = 0.08 м Задача 298.Кольцо a радиуса R, установленное на неподвижной горизонтальной оси B радиуса r, было сообщено в начальный момент угловой скорости (o0. Да.) Идти на задание 298. Решение. Предположим, что кольцо А находится в контакте с вращением. Ось Li в точке C. внешняя сила приложе
на к кольцу. P-вес кольца, N-нормальная сила реакции оси, c-сила трения скольжения кольца по оси: b . С= /Л ’ = / Р, перпендикулярно нормальной реактивной силе N, направленной в противоположном направлении к движению. То есть горизонтальное направление светло-желто-коричневое. Выберите направление вращения кольца, то есть направление отсчета угла поворота по часовой стрелке r. R1 и m = — \ r. r’I получается. И затем… Предположим, что вес кольца равен P = fgr. (Р * — Р2) являются: = — Р1) — о «) н Из уравнений (2) и (3) уравнения подставляются значения y] tg и 1g * = Я (I), мы находим: где Начальные условия движения следующие: Т = 0 СР = 0,)• БЖ-4fgr
Число оборотов, выполненных до остановки кольца、 Эта задача также может быть решена с помощью теоремы об изменении кинетической энергии материальной системы(см. Решение задачи 349.Существует также сравнительная оценка обоих решений.) Задача 299.Угловая скорость объекта начинает вращаться из стационарного состояния, под действием силы пары моментов, зависящих от вращения O: MZ = in {) — af -, где/ / z0 и a-константы. Где mQ-крутящий момент, а<2 $ * — тормозной момент. От решения
Решение. Вид дифференциального уравнения для вращения твердого тела вокруг неподвижной оси имеет вид л / .? = 2 МЛП). К твердому телу приложена внешняя сила: P-вес, сила, поддерживающая реакцию, пара сил момента t2.Поскольку момент веса и сила реакции опоры на ось вращения z равны нулю, то сумма момента внешней силы на ось вращения^^равна моменту mz>. н 2 «,(л)= я, — АФ * Итак, дифференциальное уравнение вращения принимает вид: Или Если вы замените £на-j и разделите переменные, вы получите: 14 л Ви? ; = — о- Если вы интегрируете это уравнение, вы увидите следующее: ’|/Т, N — ’ Т + с 2 В » > О!/ В0.ЛЗ•[Т]» * Если £= 0, 9 = 0, то C = 0, т. е. 1 / ^ Ж.-6 Джи? 2 / — в. 1П — — — — — = в Флорида / Флорида {] Т. Y —— Решите это уравнение для получения требуемой угловой скорости вращения
твердого тела i = V’t — Джей-ВНМ ^ л 1-ф- Два —- — Джей-МВВ ^ Т 1г Для решения поставленной задачи применим теорему об изменении углового момента точки масс относительно оси Z. К (О Он показывает вес массы P и силу реакции нити накала. момент силы реакции нити R относительно оси z равен нулю, а весовой момент P равен-Ph-PI sin = Проблема 300.Твердое тело начинает вращаться вокруг неподвижной оси r в неподвижном состоянии под действием силы пары моментов, зависящих от угла поворота a 0). Если момент инерции к оси вращения g равен lz, то находим уравнение вращения твердого тела. Центр тяжести твердого тела находится на оси rotation. At в первый момент твердое тело было неподвижно. Решение. После записи дифференциального уравне
ния для вращения твердого тела вокруг неподвижного естественного по r: я / я = с v > η(к)、 вычисляет главные моменты внешней силы относительно оси Z. Потому что масса твердого тела с моментом силы опорной реакции равна силе пули、 н тг = м2 + ТМ * = а-грех КТ-АБ. Я Так… l $ = a sin kt-a$; это уравнение записывается следующим образом: Ноль) ПФ = Т грех КТ、 л / 1 Где: 8=, — и y = 7 -.Общее решение этого производного урана ’Р’ Решение является суммой общего решения cp, соответствующего однородного уравнения, и основного решения o2 уравнения (I), то есть
ГТГ грех КТ, потому что КТ. (4 )) Осталось определить интегральные константы Q и C. для этого выделим соотношения (4) относительно времени. ? — С & R «—^ УГ, потому что КТ-1-кт грех. (Я) После замены начальных условий упражнения: (4) в£= 0、-^ = 0、(используйте I = 0, 9 = 0 С (o), чтобы получить систему уравнений. 0 = С.- }—, о == — С4? -к т> л. Когда вы решите эту систему уравнений, вы можете увидеть: Г-т-и Г — Ч — ^ ^ ^ (кг (ИС) Подставляя значение Cj в уравнение(4), получаем уравнение вращения рассматриваемого твердого тела вокруг неподвижной оси. ф = Я-Е «Ф’ — л ^ ТФ (грех КТ + * с
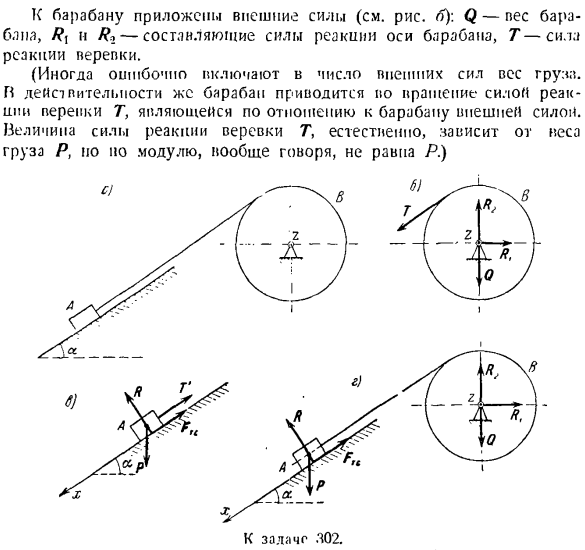
Куда? Проблема 302.Когда лопасть Р груза а опускается вниз по наклонной плоскости, барабан в поворачивается канатом, обернутым вокруг барабана В. g-радиус барабана, f-коэффициент ползучести, который заставляет груз скользить по наклонной поверхности угла а относительно горизонта. 12-момент инерции барабана относительно вращения естественного по g, вертикальный! О, на поверхности рисунка. Определяет скорость вращения барабана. Вес веревки игнорируется. Решение. Эта задача может быть реше
на с помощью дифференциального уравнения для вращения барабана B вокруг неподвижной оси Z. н IJ5■■ = X Л. Дж. Внешняя сила приложена к барабану(см. Рисунок если t = 0 6 = 0, следовательно C = 0.So угловая скорость вращения барабана равна рп (грех — / соз а). ? = — 77-л- 1 *- \ — р * с Эта фигура была создана в предположении, что маятник движется в направлении увеличения угла поворота =μ, 1r =и д пт = Т%(3) dt н подставим значение η (Fk), а из формул (2) и (3)
уравнения k = I Пирог (1), Получить ниже. Мп:\—л / грех 9、 Или ?- sin 9 = 0 g(4) Решение этого нелинейного дифференциального уравнения колебаний маятника сопровождается определенными трудностями. Поэтому мы решаем задачу приближенно, предполагая, что вибрация маятника мала. Преступление 9 продолжается sin9 = 9-ed-1-5-••• И если вы игнорируете термин расширения с более высокой степенью, чем первый, вы получаете грех 9.Тогда дифференциальные уравнения и малые уравнения колебаний маятника принимают вид: 9 +?- 9
= 0. Я отметил последнюю запись.: 9-f&* 9 = 0. Эту проблему можно решить и другим способом.»Применить теорему об изменении главного момента импульса системы миэпу, связанного с естественным по?: ■ к = 2 <•-) к =: Поскольку эта материальная система состоит из барабана R и груза A, то реактивная сила t}каната является внутренней силой, поэтому она не входит в уравнение (5).Это позволяет системе уравнений исключить T и x(1)、(2)、(3)это облегчает решение проблемы, потому что вам не нужно использовать какие-либо другие инструменты. После вычерчивания всех внешних сил системы: P, A*, c, Q, Ri и^(см. Рисунок D), составьте сумму моментов внешних сил относительно оси Z. н тг (Е «К)=
пр ЗША-Пт пр = пр(грех * — / соз а).(с) И= Я (Формула (b) не включает момент составляющей массы P, равный модулю Psina, который направлен вдоль каната, компонент массы P перпендикулярен направлению каната, равному модулю P cos s, а встречная сила R-P cos формулы (6) нормальной поверхности имеет противоположное направление, равное модулю p cos s).) основным моментом импульса системы, состоящей из барабана и нагрузки относительно оси z, является формула Я-J_ / 21 Л2-ЛЗ-Джей. Где l’j} — момент
импульса барабана, а/ _ / ’ — момент импульса груза относительно оси Z. У нас есть: Р П Л? =- ВР = — из РФ(в = ЧХ-РР). С-8 Кроме того, L’z ’ =Iz§. So… н Подставим значения^ mz (Fck) и Lz из выражений (6) и (7) выражения Я Песня(5), мы получаем: [] р л ха? = Пр(грех — / потому что)、
Отсюда следует Формула(4).Если в дальнейшем повторить решение задачи, как в первом варианте, то вы увидите следующее: гр(грех 2 — / соз а) вопрос — составляющая силы реакции оси усиления маятника. Используйте дифференциальные уравнения для вращения твердого тела вокруг неподвижной оси. Я, она-О.) А — = — Я Следовательно, момент силы и момент усиления r на оси равны нулю. л ^Да, (K)=™2 (P)+да, (Q)= — p грех? — выражению (I)из выражений(2)и(3)、 к-я Мы получаем: П / а-я»,».. 192 4 ″» см Или 528 а. Предполагая грех, рассмотрим малую вибрацию маятника. ^ Дифференциальные уравнения колебания маятника Нравится Маркировки Перепишите
полученное уравнение следующим образом: 9 4-кли = 0. Характеристики форма урависпие равна 0.Его корни: }.4 = _l, за ки. Результат. ? = С, потому что КТ -] — с * грех КТ. (6) Мы разберемся с этим.: 6 = — Cxk грех КТ-П-С * К, потому что КТ. (7 )) Начальные условия движения маятника принимают вид: Для£= = 0? =?»»? =?о- подставляя f = 0, 9 = в (6) и/ = 0, φ= в (7), C.?0, С2=.Если вы введете эти
значения в уравнение (0), то увидите следующее: СР <З0 потому что КТ грех-л Вводится следующая нотация. <p = < 2 Син-ФА)、 И затем… То есть, физический маятник совершает гармонические колебания. Угловая ширина вибрации a, которая определяется из системы уравнений (I), равна、 Она зависит от начальных условий движения и круговой частоты колебаний. Начальная фаза колебаний a найденная из той же системы уравнений имеет вид: Это также
зависит от начальных условий движения и круговой частоты вибрации. Частота круговых колебаний от k = L /(см. уравнение (o)) Не зависит от начальных условий движения. То есть в случае малых колебаний (sincc ^ s) физический маятник обладает свойством изохронизма. (Рассматривая математическую задачу 284 колебания маятника, мы получили формулу для круговой частоты колебаний маятника с конечным углом amplitudes. In в этом случае маятник обладает свойством изохронной лжи, период которой зависит от угловой амплитуды колебаний.)
Чтобы определить местоположение центра качания конкретного физического маятника, необходимо учитывать, что центр качания находится в стороне от точки поворота О на расстоянии укороченной длины физического маятника (помните, что математическая длина окружности частоты колебаний этого физического маятника называется величиной, не зависящей от длины окружности).) ) В процессе решения задачи о математических колебаниях маятни
ка (см. задачу 2С4) была определена частота его круговых колебаний. Р & Р.. / / < / g = y для рассматриваемого физического маятника, k = I /. Выравнивание квадрата круговой частоты сокращает длину 553. Физический маятник/ пр = ^ /. В результате центр K этого физического колебания маятника находится далеко от точки усиления O (см. Рисунок). Охо Для решения этого линейного однородного дифференциального уравнения второго порядка с постоянным коэффициентом необходимо создать соответствующее характеристическое уравнение L. » — j-k * =0.Корин
характеристического уравнения является,.2 = Ил / U и решение уравнения описывается следующим образом: СР = С, потому что КТ С2 грех КТ. (5) Для определения интегральных констант C1 и C2 используют начальные условия заданного движения. Рассматриваемое условие указывает на то, что в первый момент маятник, в котором напиток занимал вертикальное положение, был извещен толчком с начальной угловой скоростью<0, то есть/ = 0 секунд? =(), <Ф = <ф0. Он дифференцирует = — Cxk грех лит-Ф-CJt потому что КТ. (6) Начальные условия для дисковых движения Т =
0, СР = 0, Фи = nn0. (о) и (6) назначение начальных условий упражнения является、 С,= О, С,= * 0.Таким образом, диск на проволоке совершает крутильные колебания по закону. < £ > =2s2sin КТ, к Круговая частота вибрации и угол Диск вибрирует плато. Если вместо диска на проволоке подвешено твердое тело, то его Момент инерции неизвестен, но этот момент инерции можно
определить экспериментально методом кручения vibration. To для этого нужно вычислить модуль упругости проволоки c и измерить период колебаний t подвешенного твердого тела. Фактически, в этом случае уравнение(4) принимает вид: =- Где r-искомый твердый момент инерции. Это уравнение можно записать в виде: Где кг = -.- .Круговая вибрация частота k и период 4 л * ы Bapiy T связан с Формулой k =и выглядит так: p-здесь
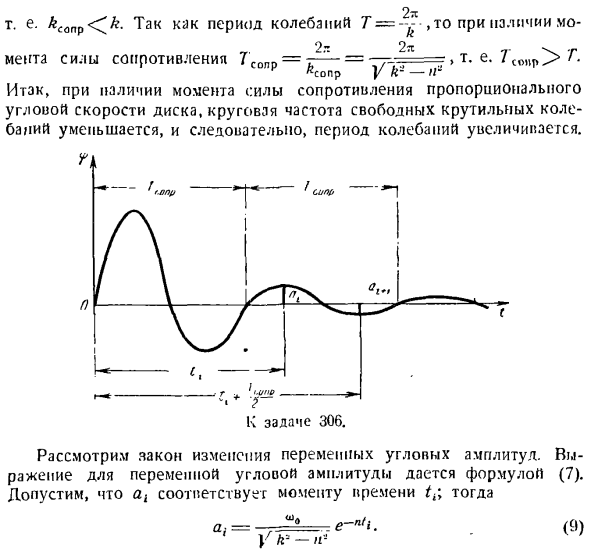
Выпуск 306.Решите предыдущую задачу, исходя из предположения, что диск вибрирует в вязкой жидкости, а момент сопротивления движению пропорционален угловой скорости диска. Определите закон вибрации диска. Solution. In в связи с предыдущей задачей добавляется момент сопротивления t *.Его знак противоположен знаку угловой скорости f. So, правая часть дифференциального уравнения (4) предыдущей задачи содержит следующие члены: m
* = — уравнение принимает вид: = 0) т. Т и ПФ * т я лд2 Т-• ^ = / r ’ 2 и^ == 2 /?При наличии следующего получаем дифференциальное уравнение свободного крутильного колебания диска. Величина сопротивления угловой скорости i и движения пропорциональна диску: $ + У + =(2) Вид характеристического уравнения X * 2lX k * = 0, тела которого равны Х12 = — Н〜±Г Н * — К » (3) Здесь это возможно в 3 случаях. а)n <^ k-для низкого сопротивления、 b) n ^> k-для высокого сопротивления、 c) n = k является ограничительным
случаем. Мы рассмотрим все 3 случая по порядку. а)n <^ K(для низкого сопротивления).Кроме того, выражение (3) принимает вид X =-Zhi \ / kl-ri. Законы движения K(для высокого сопротивления). Согласно формуле (3), корень характеристического уравнения является вещественным числом: А | = — н-[/ н *-/ р= — 11-ф — \ ч * — а». Законы движения могут быть записаны следующим образом. =(11) после вычисления производной по t £= XyCyCi * KCifi **(12) И если
мы подставим начальные условия = = 0 для движения, (11) для-p = 0 и (=) для/ = 0, φ= 10: г-г- L1 2 Если ввести результирующие значения C и C2 в Формулу (11), то получится: ? =(13) Здесь.__ л {=- н-Н * — Л’1,> .4 = — п-(- г-в- поскольку t — > co, величина
k) диск будет иметь затухающее, непериодическое движение. o) n = k (предел случая). Согласно формуле (3), тело характеристического уравнения будет равно X,= X*= -//.Законы движения 9 = С, Е-Рие + Cxte ’ НЛ. После вычисления производной? т. 9 = — pCxc-т-ф с.2В-НТ-nC4e (14) — номер. (15 )) И заменить начальные условия движения:£= 0,
= co0 Если ввести значения C \и C *, полученные в (14), то получится: (1г) 9 == я%ТК-НЛ、 Где n-это
как и / — > uc, выражение (16) становится неопределенностью в виде ω * 0, поэтому мы применяем правило Лотара для выявления неопределенности. — Л / _ _ _ Ю _ _ <В » М Лиин?= Лим * округа = лирн 5■ Лим Лим-а、 С-ГКП/-* 00 / −00 * я-чч {тр> я * г. E. In в крайних случаях ( / / = = & ) диск будет иметь затухающее и непериодическое движение. Так: a)для низкого сопротивления, диск Демпфирование вибрации по закону: φ= — е ’НТ грех / / Р’ 2-н * /、 Я АС к = 2р МК-р » р = з> б) в случае высокого сопротивления(n ^> k) диск совершает затухающее непериодическое движение по закону. е = — _ _ _ е рт (
ЭВН *—с — ки ’)、 Куда?- в) в крайних случаях(n-k) диск совершает непериодическое движение, которое распадается по закону. <Р = У ^ Е-НТ、 Здесь.//-、 Выпуск 307.Когда диск входит в контакт с упругой проволокой, возникает крутильная вибрация occurs. In в этом случае нижнее основание диска находится в контакте со стационарной горизонтальной плоскостью (см. рисунок).Максимальная сила трения в нижней части диска 0, несущая поверхность равна t «’ max = 10
кг-см. Упругий момент проволоки пропорционален углу скручивания cp. 1 рад \ с = = 50 kg-cm. At в первый момент диск поворачивается на следующий угол. 1, который был выпущен без первого курса. Если момент инерции для оси r, проходящей вдоль проволоки, равен l = 0,5 кг, то определяют число и величину угловой вибрации ширины вибрирующего диска до упора. см секунд 1. Решение. Крутильная вибрация диска ослабляется за счет наличия моментов трения. Движение останавливается в крайнем положении disk. In в этом положении момент трения больше, чем момент упругости проволоки. Решение этой задачи осложняется тем, что при изменении направления вращения диска изменяется направление момента сил трения. Так как сила трения является постоянной
величиной, то необходимо изменить знак дифференциального уравнения колебаний забоя. Поэтому при движении отдельно в каждом направлении(по часовой стрелке и против часовой стрелки) необходимо создать дифференциальное уравнение диска oscillations. In в этом случае значения угла поворота и угловой скорости диска в момент, когда это дифференциальное уравнение теряет свою силу, будут начальными условиями последующего дифференциального уравнения. ^> Точка отсчета угла поворота < p короткого диска
в положении, где момент упругости проволоки равен нулю. Обратный отсчет вращения диска 9 против часовой стрелки считается положительным (наблюдатель будет считать, что он смотрит вниз на диск с края оси z). Он прикреплен к диску. P-вес диска, R-сила реакции проволоки, t2-момент упругости проволоки и момент трения нижнего основания диска в неподвижной горизонтальной плоскости. Максимальный модуль для этого момента равен\ tr \ pmx. Для решения этой задачи используются дифференциальные уравнения
для вращения твердых тел вокруг неподвижной оси Z. Л =£МХ (Фэк). k = I Семьдесят семь Р К выпуску 307. В первый момент диск повернулся против часовой стрелки на угол — / t \ jmax, то есть 0,5? = = — боавр + 10 или ?- /-100? =20.(1) Дифференциальное уравнение (1) представляет собой движение диска по часовой стрелке при начальных кинетических условиях:/ = 0 М = 0. Общим решением этого дифференциального уравнения является сумма общего решения соответствующего однородного уравнения и частного решения уравнения (1), то есть<p = cp, — [- cp2.
Смотрите также:
Предмет теоретическая механика

