Теорема о взаимности работ и перемещений.

Теорема о взаимности работ и перемещений ,

Взаимность Во-первых, начнем с задачи, что балка свободно лежит на 2 опорах и показана на рисунке. Определите отклонения в 298, a и b. Это отклонение получается путем подстановки x-го в Формулу (86). Нагрузка P действует в точке C. 0. Рисунок 298. Pbd (год） Это указывает на то, что замена b на d и dt на b не изменяет это уравнение. 298.6, отклонение D, отклонение D и то же 298 a. получаем 298.6 Рис. из рисунка.

При простом повороте луча на 298, 180° точка C совпадает с точкой D, а точка D-с точкой C. Таким образом, на фиг. 3 C прогпб 298, S равно прогибу фиг. О. 298 а. это означает, что если нагрузка Р перемещается из точки С В точку О, то отклонение, измеренное в точке О в первом случае нагрузки, будет таким же в точке С во втором случае. Это особый случай взаимности.

Для того чтобы вывести теорему в общем виде 1, рассмотрим упругое тело, нагруженное двумя различными способами, как показано на рисунке 299, и поддерживаемое таким образом, что оно не может двигаться как твердое тело. в начальном напряженном состоянии приложенные силы находятся в состояниях Px и Pb P $и P4.In в первом состоянии точка действия движется в направлении действия силы: b » 6 «6, b4, а во втором-6′, b’, 6′, b^.

Сила 1-го состояния при смещении соответствующего 2-го состояния действие равно работе, проделанной силой 2-го состояния по отношению к соответствующему движению первого * символически это выражается как:：〜、 Рисунок 299. Чтобы доказать эту теорему, рассмотрим энергию деформации тела, когда все силы Р19. 。 。 , Р4 действует одновременно, пользуясь тем, что величина энергии деформации не зависит от порядка, в котором приложена сила, а только от конечного значения силы.

Для первого метода нагрузки сначала применяются силы Px и P%9, а затем P9 и RA. Потенциальная энергия, накопленная при применении Px и Pv, равна П-и+ С -£• -,<а） Работа, выполняемая силой при применении Р9 и Р4、 ^ 4-^ *•(Б） Однако, если вы хотите применить очки Rzh и RA、 * −1/ * )

Частным случаем этой теоремы является J. C. MaxwelPoM(cit. То. 286).Теорема E. B e 11 принадлежит I, Nuovocimento, ser. 2, т. 7 и 8, 1872.In в более общем виде теорема была дана Lord’om R e leig b’em, Prgos. Лондонская математика. соц., Том.４８７３; または научные труды 、 Vol。1, стр. С. 179.

Различными приложениями к решению технической задачи этой теоремы являются: O. By M h g * Ohm и H. Это было сделано около M u 1. I Р-Бреслау (цитируется по стр. Ранее приложенные силы Px и P идут к 6’.Затем Px и Ry выполняют работу 。 ^ ^ ^ ^(с） Итак, если вы суммируете (А), (Б) и (в), вы увидите общую потенциальную энергию, накопленную в теле. -я ПП + ^ п + ^ п + п + па + па-(<3） Для 2-го метода нагрузки мы сначала применяем силу P9 и P4, а затем Px и P%.

Тогда повторите предыдущий аргумент, чтобы получить следующий. 。 P / > 1 P/> .РА. Яд. Г + РА + ^ А- <> Обратите внимание, что уравнения (b)и (f) должны представлять одинаковое количество потенциальной энергии, и вы получите формулу (206), которая представляет теорему взаимности. Эта теорема может быть доказана против любого числа сил, а пары или пары с forces. In в случае пары, соответствующий угол поворота используется для перемещения.

В этом частном случае в начальном напряженном состоянии действует 1 Сила P, а во 2-м состоянии для 1 силы P8 формула (206) равна 2） РГК-РА-(207） ■я 4. * 4- Если Pi = Pa, Tb b, ’ = b2, то есть движение точки действия силы P в направлении силы P, вызванной силой P, равно движению точки действия силы P в направлении P, вызванном силой P7.Подтверждение этого вывода уже было сделано по поводу особого случая балки, который показан на рисунке. 298.- -В качестве другого примера рассмотрим изгиб балки, которая свободно лежит на 2 supports.

В первом состоянии согните с центральной силой P, а во втором-с парой M Конец. Сила P создает угол наклона в конце, а пара M, приложенная к концу, вызывает отклонение в середине уравнения. Силы Px и Pr остаются постоянными, поэтому эти формулы не делятся на 2.

Формула(207)принимает следующий вид — насчет Кларенса. Людмила Фирмаль

Точка, в которой точки приложения перемещаются в B и’. * ) Это J, S. впервые доказано Максвели’ом и часто называется теоремой маджуэ. Теорема взаимности работы и перемещения может быть очень полезна в задаче нахождения наиболее неблагоприятного положения движущейся нагрузки в статически неопределенном состоянии. structure. An пример-схема. 300 показывает балку, где один конец закрыт, а другой поддерживается свободно и поддерживает сосредоточенную нагрузку R. 

Левая опора при изменении расстояния нагрузки x от этой опоры. Получить фактическое состояние балки (рис. 300, А) в качестве первого состояния нагружения. На рисунке показано 2-е или фиктивное состояние. 300.6 внешняя нагрузка и чрезмерная поддержка отбрасываются и заменяются Рисунок 300.

Найти изменение размера реакции X-{ Известная реакция X добавила восходящую силу, равную 1.Это 2-е состояние нагрузки определяется статически и может определять соответствующую кривую оси балки(уравнение (97), стр.* см. 134).Если оси координат приняты, как показано на рисунке. 300, 6, затем• я ^ ту-Яф + х）- (0 6-отклонение ребра, а y-отклонение расстояния x от левой опоры.

Затем, когда применяется взаимность, работа, выполненная силой 2-го состояния до соответствующего перемещения 2-го состояния, является ХВ-Ру. При расчете работы, выполненной силой 2-го состояния, обратите внимание, что в конце есть только сила, равная единице (1), а соответствующее смещение точки А в 1-м состоянии равно нулю.

Таким образом, эта работа равна нулю, а взаимность дает: •: ХВ-Ру = 0、 Откуда? Если нагрузка P меняет положение на балке (рис. 300, А), то можно видеть, что реакция X пропорциональна соответствующему значению y на рис.3. 300, b. As в результате кривая оси 2-го луча ’)

Так как соответствующее движение равно нулю, а соответствующая работа равна нулю, то реакция в готовом случае не учитывается ни в том, ни в другом случае. Состояние (уравнение (0) полностью показывает, как X изменяется с x. эта линия называется линией влияния или линией влияния реакции X).

При отображении на балке. Рисунок 300, и несколько нагрузок действуют одновременно, а затем используют эту формулу вместе с принципом сложения действия силы Где yn-ордината линии удара, соответствующая точке приложения груза Pn, а сумма распространяется на все грузы.

• Задачи 1. Создать линию влияния для опорной реакции балки, лежащей на 3 опоры(рис. 301). The solution. In для того чтобы получить линию влияния на реакцию промежуточной опоры, примем фактическое состояние нагрузки, показанное на рисунке. 301, а, первое состояние. 2-е состояние показано на рисунке. В образах, ６、 в вышеупомянутой промежуточной опоры, нагрузка P отбрасывается, реакция х промежуточных опор, 単一に等しく上向きの力に置かえられることができる。 2-е состояние нагрузки определяется статически, ось Кривой Балки известна(уравнения (86) и (87), стр. 129).

Следовательно, отклонение 5 и Вы можете рассчитать. Тогда работа, проделанная властью 2-го государства против соответствующего движения во 2-м государстве, будет равна ХБ-ру. 。 ■ идентификатор. Так… Работа силы (силы, равной 1) 2-го состояния при соответствующем смещении первого ТТ. / Состояние (C имеет нулевое отклонение) равно нулю. Отсюда^^ 0 о ХВ-ру = 0, х = П Рисунок 301.As в результате кривая оси 2-го луча Плавление придает форму реакционному воздействию lines.

Для того чтобы получить линию влияния на реакцию опоры B, необходимо принять состояние, показанное на Рис.2 для 2-го условия нагрузки. 301, С. • 2.Используя линию влияния предыдущей задачи, определите реакцию B, если нагрузка P находится в середине первого пролета ( * = / , / 2) (рис.301, а). Ответ. Реакция направлена вниз и равна 3п 1г г. 16 UFC、 8. Найти линии влияния изгибающего момента на центральную стойку с балки в 3 распорки(рис. 302).

Используя эту линию влияния, рассчитайте изгибающий момент M и когда нагрузка P находится в середине 2-го пролета. Решение. Первым состоянием нагрузки является фактическое состояние с изгибающим моментом, действующим на участок с (рис. 302. а) есть. * ) Использование модели при определении линии влияния было разработано G, E. например, g s * om, J. Franklin Inst. Одна тысяча девятьсот двадцать семь、

Во 2-м состоянии нагрузка Р разрушается, балка срезается в сечении с, 2 пары равны 1 и направлены в противоположную сторону, заменяя МС(рис. f302. 6).Этот случай может быть определен статически. Углы b и 0 определяются по формуле (104), а отклонение y определяется по формуле (105).Сумма углов 0 и 0B представляет собой смещение изгибающего момента M & соответствующего состояния 2 для действия в 1-м состоянии.

Работа, выполняемая силой 2-го состояния по отношению к смещению первого, равна нулю, так как фактически отсутствует надрез на опоре С, а движение, соответствующее 2 парам, равным 1 из 2-го состояния, равно нулю. Отсюда И затем м ^ рн-(б> Поэтому при изменении нагрузки P 6.Когда груз Р движется вдоль балки Б, ничья сила X линейный воздействия на горизонтальной штанги Сиджея (рис. 303, п).

Работа, выполняемая силой первого состояния до соответствующего смещения 2-го состояния, равна x Людмила Фирмаль

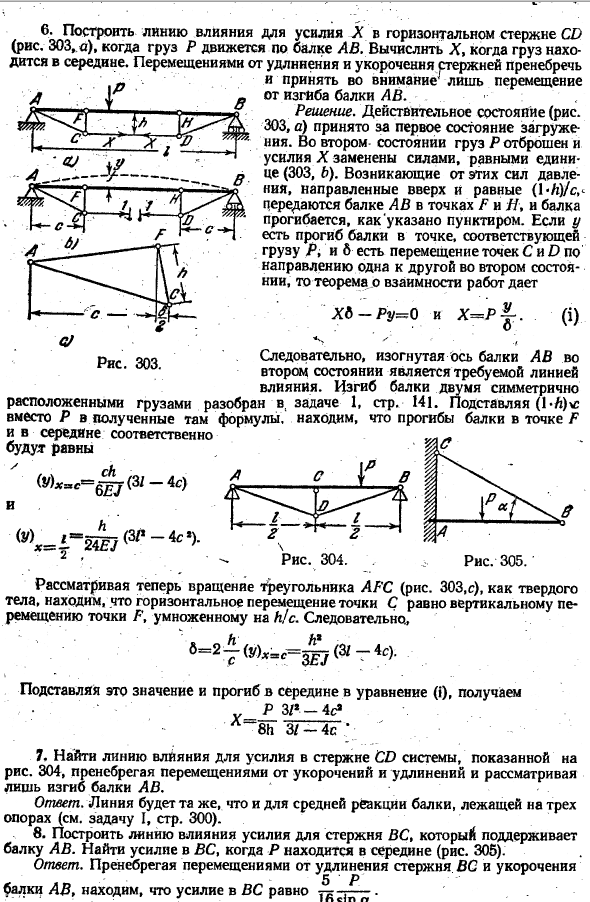
Вычислите X, когда нагрузка находится в середине. Смещение от стержня растягивается и укорачивается. И рассмотрим только 1 движение d U 1 «’» от луча изгиб. В.- ’、 D ^ГГ1і решение. Фактическое состояние(рисунок ^ 03 ″ e) принято 33 первое состояние читается!。 C9 X * x. во 2-м состоянии нагрузка P отбрасывается.、

Сила X заменяется силой, равной единице (303, b).Давление, возникающее в результате этих сил, равно (*I)/ s вверх и передается на балку AB в точках P и Z. Балка изгибается, как показано пунктирной линией. если y имеет отклонение луча в точке, соответствующей нагрузке I, А B находится во 2-м состоянии и точки C и P перемещаются в одну сторону в другую, то теорема взаимности имеет вид: 1.： Xb-Ru = 0 и X = P (I).

Поэтому криволинейная ось 2-го состояния луча AB является искомой линией воздействия. Рассмотрен изгиб балки с 2 симметрично расположенными грузами. Выпуск 1, 141 pages. So подставляя усы (1-L) вместо р в полученную формулу, отклонение луча в точке Р Рисунок 303.

Теперь, если рассматривать вращение треугольника АФК (рис. 303, в) как сплошное тело, то мы увидим, что горизонтальное смещение точки С равно вертикальному смещению точки F, умноженному на h / C. Поэтому、 6 = 2 (г)* = с.= 3gj(3и-4С). Подставляя это значение и центральное отклонение формулы (I), получаем:’, * P 31 * — 4s*. 8ч 3 / −4 секунды.•; 7.

Найдите линию влияния мощности стержней системы CD, которая показана на рисунке. Рассмотрим только изгиб рекламной балки, игнорируя движение из-за деформации, укорочения и удлинения. Ответ. Эта линия будет такой же, как средняя реакция балки, которая находится в 3 стойках(задачи I, стр. 8.Балка АВ для построения линии удара стержня переменного усилия по опоре. Найти мощность самолета, когда P находится в центре(рис. 305).

Ответ. Пренебрежение движением из-за удлинения и укорочения стержня самолета 5 ^ ^ В случае луча AB можно видеть, что сила самолета равна:

Смотрите также:

Предмет сопротивление материалов: сопромат 

Исключительные случаи	Деформация ферм
Чистый изгиб кривых брусьев	Приложение теоремы Кастилиано к решению статически неопределимых задач