Оглавление:







Теорема о трёх моментах
- Три мгновенные теоремы. Для вывода трех моментных теорем возьмем ряд пролетных строений разной длины и сплошную балку как 1X то, что требуется при вертикальной нагрузке(рис. 372, а). Сначала нарисуем все реакции, которые могут быть в этом случае; из условий равновесия ясно, что горизонтальная реакция/7o=0. Я / gtt1B gttp bl_J Ulrmrhtik/л Пятый Я? Ш / А ШЯ а) Фигура. Триста
семьдесят два АГ ТА Для получения этой базовой системы (рис. 372, b), поместите шарнир в опорную секцию. Дополнительными неизвестными будут опорные моменты над промежуточными опорами M1G L42, D43… Экстремальный момент на опоре равен нулю. Загружайте систему внешними нагрузками, помогая сэкономить время. 372, в). Поскольку направление момента поддержки нам неизвестно, мы предполагаем, что они положительны.
При разрешении, символ результата указывает, является ли предположение является правильным. Здесь необходимо сделать Людмила Фирмаль
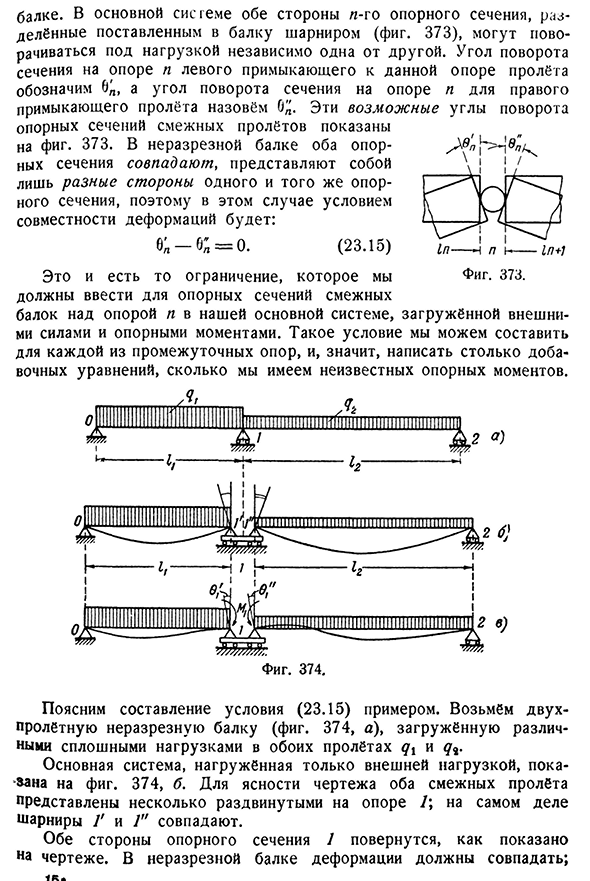
условия, чтобы ввести те же ограничения на деформацию основной системы, и это доступно в непрерывной теореме§ 144]и трех моментах 451. Опорный пролет и для прямых углов поворота В основной системе балки обе стороны l-ой опоры разделены шарнирами, расположенными на балке(см. рис. 373) могут вращаться под нагрузкой, независимо друг от друга. Угол поворота секции на левой опоре N, примыкающей к этой, указывает 6D, а угол поворота секции на опоре соседних пролетных строений называется 0^. Эти возможные опоры соседних пролетов показаны
на рисунке. 373 поперечное сечение только для ризоидного поперечного сечения, совместимого В сплошной балке обе опоры совпадают и представляют собой одинаковые стороны, поэтому в этом случае происходит деформация: е; — б; = о. Те же условия поддержки(23.15) C2Q / ЛН—- — 1 п — — — — — — ЛН+1 Это предел, который мы считаем. 373 наши основные КЭ нагружены внешними силами и опорными моментами такие условия могут быть выполнены для каждой из промежуточных точек опоры и, следовательно, могут быть записаны многие дополнительные уравнения с неизвестными
- опорными моментами. Позвольте объяснить положения условия (23.15) на примере. Возьмем двухпролетную сплошную балку(рис. 374, а) нагруженный с различными непрерывными нагрузками в обоих пядях qx и q^. Основная система загружается только внешними нагрузками и показана на рисунке. 374, Б. для наглядности рисунка оба соседних пролета выражены несколько раздельно на опоре 1\фактически шарнир G и 7 ″ совпадают. Как показано на рисунке, обе стороны опорного участка 1 вращаются. В непрерывной балке деформация должна совпадать; 16 * 452 статически неопределенная балка[гл. XXV Это может быть достигнуто путем загрузки
отрицательных опорных моментов в основную систему. 374, В) для достижения этого соответствия и выбора его размера; однако для этого соответствия основной вариант системы должен удовлетворять условию(23.15).): б;b; ’ =0. Кроме того, следуя плану расчета статической неопределенной балки методом сравнения деформаций, возвращаемся к схеме рисунка. 372, мы должны расширить формулу (23.15) путем вычисления величины деформаций, содержащихся в ней. Угол поворота основного системного сечения опоры Р зависит только от деформации соседних пролетов 1Р и / dy1. Различим эти два пролета и все нагрузки, действующие на них рис. 375).
Натянуты 1P на внешние силы, расположенные в преступлении, и опорные моменты Mp_g и MP; span/in + 1 задействованы внешние опорные Людмила Фирмаль
моменты MP и L1D, действующие в стороне+1. Чтобы прояснить рисунок, оба соседних пролета находятся в некотором отдалении в поддержку p\на самом деле, петли и » и » одинаковы. Чтобы вычислить 6-й и 6-й углы, используйте метод графического анализа. Воображаемая балка, показанная ниже чертежа рассматриваемого пролета, также является шарнирной опорной балкой. Мнимая нагрузка левого пролета 1Р выглядит следующим образом: а) график нагружения участка изгибающего момента от внешней нагрузки и расстояния центра тяжести этого участка ОГ левой опоры AP \ Pro; Б) треугольник графика изгибающего момента
от положительного опорного момента) график изгибающего момента от положительного опорного момента MP. Правая антенная балка пролетом 1р а представляет собой нагрузку: а) участок изгибающего момента от внешних сил с нагрузочной зоной А) D+1 и расстоянием центра тяжести от правой опоры б) участок изгибающего момента с нагрузочной зоной в) участок центра тяжести от правой опоры В) треугольный график изгибающего момента от положительного опорного момента L1p+1. Угол поворота опорной секции N ’ левого пролета делится на боковую силу PA этой опорной жесткости для соответствующей балки-
манекена.: о-КН. боковая сила в блоке поддержки L-EJ равна реакции поддержки фиктивной балки R’N. Рассчитаем эту реакцию; грузовая зона распределяется между опорами воздушной балки по закону рычагов, переходящих в опору Р » груза, при этом треугольный груз делится на две трети и затем делится на две трети. И так оно и есть., РН=<•>» * й+я * 4М p1p+1•4= = г Mp1p Н » 4″ Мнимая боковая сила Q’ » равна этой знаковой реакции Корпус QFN = Р^ Угол поворота равен = — 6E7[6 (°l N » 2lml+ ) Аналогично получаем для правого пролета: R’N=+4-m p1p^S-боковая сила в этом случае равна опорной реакции со знаком минус: Qn= — R’N, а угол поворота 0 равен: +З н+я+.
Подставляя значение и уменьшая его на выражение=0 и QEJ, получаем следующее выражение: [Бия^4-2 мл+а-л] — б ~Г[бо>я+1~Г2^Л Л+1~г^л+/л, я]=о, или » ^Л-/Л -}-(/»С-/я+1)-г-L4ya+1/я+1= = _b г^±^2± * Ю. (23.16) L’l(23.18) это означает фиктивную поддерживающую реакцию поддержки (n)из пролета. Под средним значением R, примените уравнение Эпюры M (h)указанной нагрузки для обоих Отчет Ной балки. Встроенный в фигуру. 376, б. напишите для поддержки 1. Предположим, Что L=1. (23.16) при расчете нагруженного непрерывного трехширотного поперечного сечения, как показано на рисунке. Номер 376 поддержка слева направо. Выражение трех
моментов должно быть записано 2 раза: для опоры 1 и опоры 2. Изгибающий момент нагрузки системы должен быть нанесен на график. Уравнение Из за этих трех Внешние основного сюжета данный момент МП-1=МО=0;С»=О)=0; » Л и1 РСТ, _i_Pll.. . ls + 1= » С=Т — + — Г -, РЯ+1-БТ=Ю. Уравнение: 2A1, (A+ /4) 4 — (23.19)§ 144] теорема о моменте трвх 455 Пройдите в поддержку 2, предполагая n=2, тогда MP^=7143=0; / RP. 2,/?. одобрение. qll-Да2-я «8-’ <°л+1 — = «б У4•я г- «г Т2′ Второе уравнение третьего момента принимает вид+2L1. 2 (4+Z3)= — 4RP — •(23.20) Дополнительные неизвестные и TI2 определяются решением уравнений (23.19) и(23.20). В некоторых случаях, если вы принимаете/1 = /2 = /3 = /, эти два уравнения сводятся следующим образом: 4L41C-L42-г р/,(23.21) (23.22) Решаем их, получаем: М, — — — Пл4-40-60′ (23.23) зная значение опорного момента um — _ — P L _ _ is
— (23424), можно легко построить график момента непрерывной балки без дополнительных вычислений. Для этого нарисуйте основную систему участка сгиба Фигура. Триста семьдесят семь Крутящий момент (рис. 377, б). Фигуры изгибающих моментов от опорных моментов Mi и M3(рис. Рисунок 377, с) обозначен пунктирной линией. 377, Б; для сложения границ 456 статический неопределенный пучок [гл. XXV Ордината участка и ордината разлома должны быть нарисованы в одном и том же масштабе. Расчет характерных координат и суммарный график показаны на рисунке. 377, G. вся конструкция может быть выполнена без нажатия на опорную секцию; в этом случае это было сделано только для большей ясности.
Смотрите также:

