Оглавление:
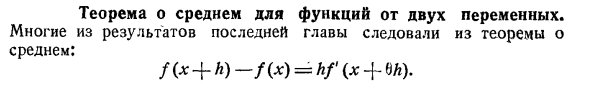




Теорема о среднем для функций от двух переменных
- Средняя теорема для функции двух переменных. Многие из результатов в последней главе следуют теореме о среднем значении. f (x + h) -f (x) = hf (x + bh). Это равенство можно записать как = / ‘(Jc + 6 & ) bx, Где у = f (х). Предположим, что z = f (x, y) является функцией двух независимых переменных x и y, давая x и y приращение A, k или bx на. Задача нахождения соответствующего приращения z выражением, т.е. tz = f (x + hty + k) -f (x, y)> Производные 2 для A, k и jc и y. Дай мне / ( + A /, + = тогда / (X + A, j, + ) _ / (, y) = F () — F (0) = F ‘(b) t
Однако, согласно теореме об абсолютных дифференциалах (см. §157), r (/) = dj (x + ht, Y + kt) = A /; (X + A;, jr + * Q + так te = / (* + , j + A) — / (, »= A /; (x + 6L, jr + No.) +Поскольку fx и f’y являются непрерывными функциями Хны, /; (X + 0Aj y + U = Mx y) + * H, k, f’y с * + bA, jf + OA) = /; (X, + 7L Где u (и l стремятся к нулю как A и k. Следовательно, теорема может быть записана как: (/; + *) ** + (/; + *.) «Y. Если bx и ty малы, e и m) малы. Результаты, включенные в (1) lz = fbx + tyy
Это предпочтительная формула. Людмила Фирмаль
Другими словами, разница между левым и правым в этом уравнении мала по сравнению с большим из bx и 8y. Я должен сказать, что «больше из bx». Возможно, что 8 * = 0 или 8y = 0. Если уравнение вида Sz = X $ x -f является «почти истинным», то X = / ‘x, μ = f’y. bz-f’xbx-f’yty = r & x + fy, 8z- \ bx- [Ay = z’bx -f r] ‘5y, Где e, v), r ‘,>)’ стремятся к нулю, когда 8x и & y стремятся к нулю. Таким образом (X-f’x) bx + ({l-f’y) by = rvdg-h bb, Здесь p и a имеют тенденцию быть равными нулю. Поэтому, если C — любое положительное число, вы можете выбрать w следующим образом: Все значения 6x и & y меньше, чем по модулю , 0) = lim * M = * (0,0)
Аналогично f’y (0,0) = cp (0,0), кроме того, ясно * = {? (0, 0) + e} * + (0, 0) +4} y, Где е *) стремится к нулю для х и у и стремится к нулю. Это соотношение эквивалентно (1) для x = y-0. Однако / x и / y не могут существовать где-либо кроме источника. Соотношение (1) можно считать определением «дифференцируемой функции двух переменных *». f (x, y) называется дифференцируемой в точке (x, y). / + KY + k) -f (x, y) = (A + α) ++ (B + rt) k, Где A и B зависят только от x и y, а e и k) стремятся к нулю как h и стремятся к нулю. Доменная дифференцируемость означает дифференцируемость в любой точке этого региона.
| Дифференцирование функций от нескольких переменных | Дифференциалы |
| Дифференцирование функции от двух переменных | Определенные интегралы и площади |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- В этом случае fx и fy существуют и равны A и B, но могут не быть последовательными. Условие, налагаемое на fx и fy в этом определении, находится между слабым условием простого существования f’x и f’y и строгим условием непрерывности fx и fy. Это определение дифференцируемости имеет много преимуществ, но для наших целей условие непрерывности для частичной дифференциации очень распространено. W. W. Young, фундаментальная теорема дифференциальных вычислений (Cambridge Math. Tracts, № II) и де ла Валле-Пуссен, Анализ инфинитезималей, вып. 1, глава
Пожалуйста, обратитесь к. III, GTTI, 1933. Людмила Фирмаль

